はじめに
オイラー角の問題点としてよく挙げられるジンバルロックですが、図解による説明に終始するものが多く数学的な説明が少ないのが現状です。
実際、オイラー角でアニメーションをつけたりする程度ならこの説明でも十分です。
しかし、例えばオイラー角ではジンバルロックが起きて、クォータニオンでは起きないのかについて、誤った説明がなされることもあり、オイラー角・ジンバルロックの性質を正しく理解するためにも数学的な意味というのは知って損はないかなと思います。
本記事ではベクトル代数や偏微分など、大学初等レベルの数学知識が前提となります。
直感的な意味
まずはよく説明されている実際のジンバルを用いた直感的な説明から始めます。
Wikipediaがとてもわかりやすいので以下に引用します。
3軸の全てに自由な運動がある場合は、機体の回転によって3つのジンバルリングのうち2つの軸が同一平面上にそろってしまうジンバルロックという現象が発生しうる。発生すると、本来3あるはずの自由度が2になってしまう。
ジンバル - Wikipediaより引用
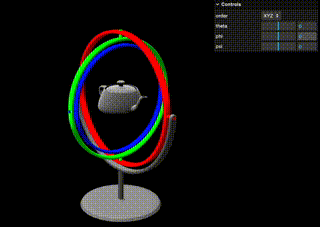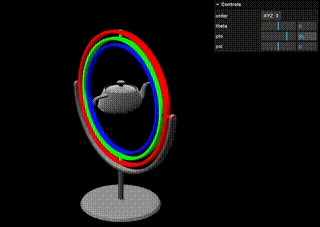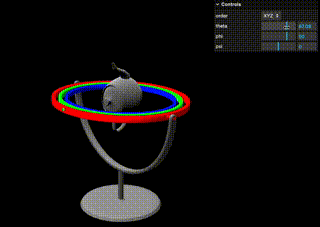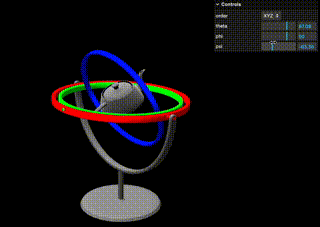
説明の通りですが、Gifにあるように一番外側と内側のジンバルが同じ鉛直方向周りに回転してしまう(=自由度が失われる)のがジンバルロックです。
また、実際にブラウザでジンバルを動かせるデモも僕の方で用意しました。
Y=90に設定することでジンバルロックを起こすことができますので、実際にお試しください。
代数的な意味
では本題であるジンバルロックの数学的な説明に移ります。
XYZオイラー角(X軸周りに角度$\theta$回転、Y軸周りに角度$\phi$回転、Z軸周りに角度$\psi$回転)
と回転行列Rの関係は以下で表されます。
R = R(\theta, \phi, \psi)= \begin{pmatrix}
\cos\psi & \sin\psi & 0 \\
-\sin\psi & \cos\psi & 0 \\
0 & 0 & 1 \\
\end{pmatrix}\begin{pmatrix}
\cos\phi & 0 & -\sin\phi \\
0 & 1 & 0 \\
\sin\phi & 0 & \cos\phi \\
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\theta & \sin\theta \\
0 & -\sin\theta & \cos\theta \\
\end{pmatrix}
この 回転行列 $R$ を $\theta, \phi, \psi$ で偏微分した時、
\frac{\partial R}{\partial \theta}, \frac{\partial R}{\partial \phi}, \frac{\partial R}{\partial \psi}
が 線形従属になる時をジンバルロックと呼びます。
またジンバルロックが発生する点$(\theta, \phi, \psi)$を特異点と呼びます。
線形従属ということは独立なベクトルが2つ以下になるので、これがすなわち自由度が失われる、という意味になる訳ですね。
具体例
$\phi = 90^\circ$ の時ジンバルロックが起こることを確認しましょう。
$R$をそれぞれで偏微分した結果は下記になります。
\begin{split}
\frac{\partial R}{\partial \theta} &= \begin{pmatrix}
\cos\psi & \sin\psi & 0 \\
-\sin\psi & \cos\psi & 0 \\
0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
\cos\phi & 0 & -\sin\phi \\
0 & 1 & 0 \\
\sin\phi & 0 & \cos\phi
\end{pmatrix}\begin{pmatrix}
0 & 0 & 0 \\
0 & -\sin\theta & \cos\theta \\
0 & -\cos\theta & -\sin\theta
\end{pmatrix}\\
\frac{\partial R}{\partial \phi} &= \begin{pmatrix}
\cos\psi & \sin\psi & 0 \\
-\sin\psi & \cos\psi & 0 \\
0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
-\sin\phi & 0 & -\cos\phi \\
0 & 0 & 0 \\
\cos\phi & 0 & -\sin\phi
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\theta & \sin\theta \\
0 & -\sin\theta & \cos\theta
\end{pmatrix}\\
\frac{\partial R}{\partial \psi} &= \begin{pmatrix}
-\sin\psi & \cos\psi & 0 \\
-\cos\psi & -\sin\psi & 0 \\
0 & 0 & 0
\end{pmatrix}\begin{pmatrix}
\cos\phi & 0 & -\sin\phi \\
0 & 1 & 0 \\
\sin\phi & 0 & \cos\phi
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\theta & \sin\theta \\
0 & -\sin\theta & \cos\theta
\end{pmatrix}
\end{split}
これに$\phi = 90^\circ$を代入します。
\begin{split}
\frac{\partial R}{\partial \theta}(\theta, 90^\circ, \psi) &= \begin{pmatrix}
0 & \cos\theta\cos\psi-\sin\theta\sin\psi & \cos\theta\sin\psi + \sin\theta\cos\psi \\
0 & -\cos\theta\sin\psi - \sin\theta\cos\psi & \cos\theta\cos\psi-\sin\theta\sin\psi \\
0 & 0 & 0
\end{pmatrix}\\
\frac{\partial R}{\partial \phi}(\theta, 90^\circ, \psi) &= \begin{pmatrix}
-\cos\psi & 0 & 0 \\
\sin\psi & 0 & 0 \\
0 & \sin\theta & -\cos\theta
\end{pmatrix}\\
\frac{\partial R}{\partial \psi}(\theta, 90^\circ, \psi) &= \begin{pmatrix}
0 & \cos\theta\cos\psi-\sin\theta\sin\psi & \cos\theta\sin\psi + \sin\theta\cos\psi \\
0 & -\cos\theta\sin\psi - \sin\theta\cos\psi & \cos\theta\cos\psi-\sin\theta\sin\psi \\
0 & 0 & 0
\end{pmatrix}\\
\end{split}
よって、
$$\frac{\partial R}{\partial \theta}(\theta, 90^\circ, \psi) = \frac{\partial R}{\partial \psi}(\theta, 90^\circ, \psi)$$
ですから、これらは線形従属であり、$\phi = 90^\circ$の時$\theta, \psi$の値に関わらずジンバルロックが起こると言えるのです。
また、この等号は$\theta$と$\psi$がそれぞれ微小変化した時にその回転が一致するという意味であり、ジンバルで確認したY=90の時、XとZの回転方向が一致するのと同じ結論が得られました。
参考
A Practical Parameterization of 2 and 3 Degree of Freedom Rotations
https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=ef5a7d668d7e246b85fc823cba06b73b0b63d4aa
3次元CGと座標系
http://www.f.waseda.jp/moriya/PUBLIC_HTML/education/classes/infomath6/applet/fractal/coord/