概要
今までは書いたプログラムが動くことを第一にしてきたので、テンプレートな記述はおまじないというか「そういうもの」としてあまり深入りしなかったが、一旦この辺りでサンプルコードによく記述されるraygenシェーダの中味について調べてみたので、記事に残してみる。
サンプルコード在り処
・Khronos公式
おそらくみんなが最初に参照するコード
https://github.com/KhronosGroup/Vulkan-Samples/tree/master/samples/extensions/raytracing_basic
・NVIDIA Vulkan Ray Tracing Tutorial
解説付きなので、非常にわかりやすい
NVIDIAはハード面だけでなく、こういった環境面でもやはり一歩先に行ってる模様
https://nvpro-samples.github.io/vk_raytracing_tutorial_KHR/#accelerationstructure/top-levelaccelerationstructure/helperdetails:raytracingbuilder::buildtlas()
raygenシェーダとは
ray tracing pipelineの出発点であり終着点。ここからrayを飛ばし、missシェーダやrchitシェーダなどを通りpixelの色を計算した後、最終結果を2Dimageに格納し、それを表示することで画面を出力する。
上図が一般的と言うかレガシーなグラフィクスパイプラインで、下図がレイトレーシングパイプライン。上図ではVertex、つまりポリゴンの頂点が中心になっており、それをパイプラインに流して(あとはAPIが計算してくれて)世界を描画する形だが、レイトレーシングパイプラインでは世界の中心はrayを飛ばす元(cameraとかeyeとか)である。そこから見える景色をそのまま計算し、2Dimageに描き出す。
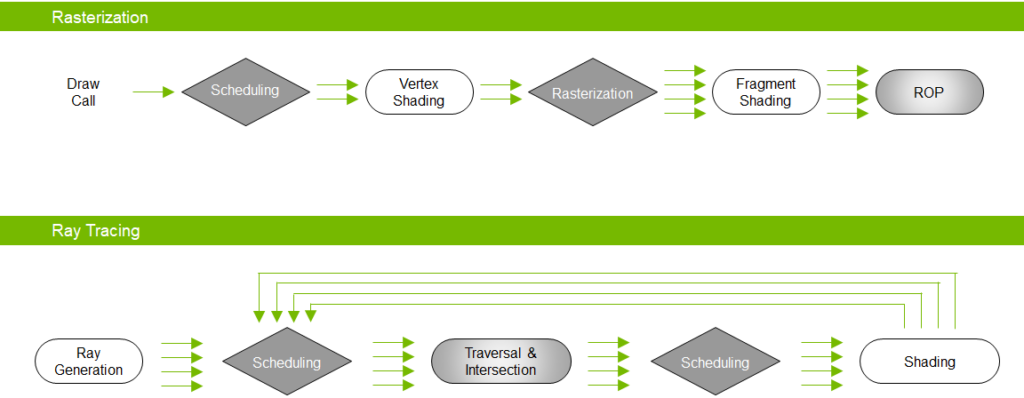
引用:https://developer.nvidia.com/blog/vulkan-raytracing/
Figure 2. Traditional rasterization pipeline versus the ray tracing pipeline
テンプレートなraygenシェーダの中味
main関数のみ抽出。シェーダは各ピクセルごとに呼ばれるものと推察できる。座標系の名前は色々あるが、下記の図の名前でここでは統一する。注意点として、これはOpenGLの図なので、座標軸の向きなどに一部誤差がある。

引用:https://learnopengl.com/Getting-started/Coordinate-Systems
The global picture
void main()
{
const vec2 pixelCenter = vec2(gl_LaunchIDEXT.xy) + vec2(0.5);
const vec2 inUV = pixelCenter / vec2(gl_LaunchSizeEXT.xy);
vec2 d = inUV * 2.0 - 1.0;
vec4 origin = cam.viewInverse * vec4(0, 0, 0, 1);
vec4 target = cam.projInverse * vec4(d.x, d.y, 1, 1);
vec4 direction = cam.viewInverse * vec4(normalize(target.xyz), 0);
uint rayFlags = gl_RayFlagsOpaqueEXT;
float tMin = 0.001;
float tMax = 10000.0;
traceRayEXT(topLevelAS, // acceleration structure
rayFlags, // rayFlags
0xFF, // cullMask
0, // sbtRecordOffset
0, // sbtRecordStride
0, // missIndex
origin.xyz, // ray origin
tMin, // ray min range
direction.xyz, // ray direction
tMax, // ray max range
0 // payload (location = 0)
);
imageStore(image, ivec2(gl_LaunchIDEXT.xy), vec4(prd.hitValue, 1.0));
}
段落ごとに見ていく。
1段落目
const vec2 pixelCenter = vec2(gl_LaunchIDEXT.xy) + vec2(0.5);
const vec2 inUV = pixelCenter / vec2(gl_LaunchSizeEXT.xy);
vec2 d = inUV * 2.0 - 1.0;
gl_LaunchIDEXTにはwindowの左上を原点とした、相対的なピクセルの位置が整数で格納されている(Screen Space)。pixel centerの位置がfloatでほしいので、0.5を足す。
次にScreen SpaceをUV空間としたpixel centerの相対位置を割り出す(inUV)。つまりScreen Spaceを(0, 0)から(1, 1)までの空間とみて、pixcel centerの位置を計算するので、スクリーンサイズ(ウィンドウサイズ)で割る。pixel centerは(0,0)から(1,1)までの値を取る。
最後に上記UV空間からClip Spaceへ変換を行う。UV空間が(0,0)から(1,1)までなのに対して、Clip Spaceは(-1,-1)から(1,1)までである。よって座標変換は
d = inUV * 2.0 - 1.0
で計算できる。こうすれば(0,0)の点は(-1,-1)へ射影され、(1,1)の点は(1,1)に射影されるので、Screen SpaceからClip Spaceへの変換が可能である。間の点は連続的に射影される。
2段落目
vec4 origin = cam.viewInverse * vec4(0, 0, 0, 1);
vec4 target = cam.projInverse * vec4(d.x, d.y, 1, 1);
vec4 direction = cam.viewInverse * vec4(normalize(target.xyz), 0);
最終的にtraceRayEXT関数でrayを飛ばすための変数を求める(origin, direction)。originはWorld Spaceでのcameraの位置のことである。これはuniform変数で外から直接与えても良いし、この例のようにviewInverse行列を与えて計算しても良い。viewInverseは後ほどまた使うので、viewInverseだけを与えたほうが効率は良いかも。View Spaceにおいてcameraの位置は(0,0,0,1)に固定されているので(逆にWorld SpaceからView MatrixによりそうなるようにView Spaceが作成されている)、cameraの位置は
viewInverse * vec4(0,0,0,1)
で計算できる。補足として、座標変換の逆行列を掛けているので、上図の変換の逆を行える。
次にdirection、つまりcameraからrayを飛ばす方向を求める。これは将来Screen Spaceに変換したときのpixel centerとなる、World Spaceの位置への方向ことである。つまりray tracingでは、すべてのピクセルに対して、それを一度World Spaceに変換し、そこにcameraからrayを飛ばして見える色を求めるということをやっている(そりゃ計算量増えますわ)。
具体的には、1段落目で求めたdを使う。dはClip Spaceにあるので、View Spaceに持ってくる。
target = projInverse * vec4(d.x, d.y, 1, 1)
View Space内での方向ベクトルを算出し、それをWorld Spaceに変換する
direction = viewInverse * vec4(normalize(target.xyz), 0)
3段落目以降
以上で求めたoriginとdirectionをtraceRayEXT関数を使ってray tracingし、rayが当たればrchitシェーダへ、当たらなければmissシェーダへの処理に進む。
最終的な結果がpayloadに格納されるので、それをimageStore関数でimageに格納し、処理完了となる。