#初めに
初めまして．今年の4月まで波動光学を専攻していた新社会人です．
前回まで波動光学における伝搬計算手法についての解説と計算結果を載せていました．
前回
今回は，計算機合成ホログラム(Computer-Generated Hologram)における物体光波計算について記述していきます．
物体光波とはその名のごとく，物体表面から回折してきた光のことです．以下に，3Dモデルから計算した物体光波の例を示します．
私のプログラムで計算しています．こちら
#ホログラムとは
「ホログラム」．一度はこの言葉を聞いたことがあるのではないでしょうか．以下のようなスターウォーズのものが有名ですね．
これは完全に空間に三次元映像を投影しています．しかし，これは非常に難しいです．空間内で光を曲げていますからね．次にアバターの画像を載せます．
このようにディスプレイの向こう側にあたかも物体があるかのように見せる技術は相当に研究が進んでいます．
「ホログラフィ」という技術であり，その成果物である「ホログラム」がこの三次元映像を実現します．
このホログラフィには大きく分けて光学系を用いる「アナログ」ホログラフィと，計算機を用いる「コンピュータ」ホログラフィがあります．
この記事ではまず，現行の三次元映像技術であるVRや3Dテレビの技術とその問題に触れた後，ホログラフィの簡単な紹介をし，コンピュータホログラフィにおける物体光波計算手法について述べていこうと思います．
現行の三次元映像技術と「酔い」
先ほど紹介したような映画にも登場したことで，三次元映像は一般に認知されるようになりました．三次元映像とは言ったはいいものの，我々はそもそもどのようにして「立体」を知覚しているのでしょうか？
人間の立体知覚における生理的要因は主に以下の4つといわれています．
- 両眼視差 は読んで字のごとく，眼球のついている位置の違いで生じる視差です．要は左目右目で見えてるものが違うので，立体として知覚するわけです．
- 両眼輻輳 は近くのものを見るときに眼球は力んで内側に大きく回転しますが，遠くのものを見るときはそんなに力みません．この力みや視線のなす角によって立体感(距離感)を知覚します．
- 運動視差 は視点を振ったときに見える部分が変化することを認知することで立体感を知覚します．
- 焦点調節 は水晶体のピントが合う位置によって立体感を知覚します．
現行の三次元映像製品の多くは「両眼視差方式」を用いますが，この方式によって正しく刺激されるのは，「両眼視差」と「輻輳」(+運動視差)です．そのため，焦点調節による奥行き感はうまく刺激されません．
特に，「輻輳」「調節」によって感じられる距離感の間には強い相関があり，これらが一致しない問題は「輻輳調節矛盾」といわれ，長時間使用による不快感や眼精疲労の原因であるといわれています．
以上の生理的要因をすべて満足し，観察者に不快感を与えない三次元映像技術として「ホログラフィ」は期待されています．
アナログホログラフィ
アナログホログラフィでは，上の図のように，被写体からの光と別に用意した光源からの光を，写真乾板のような記録材料上で「干渉」させ，その干渉縞をアナログデータとして記録します．この干渉縞を記録した媒体が「ホログラム」(この場合は特に「アナログ」ホログラム)と呼ばれます．
次に，被写体を除去し，先ほど作製したホログラムに，最初に用意した光源の光を照射し覗き込むと，ホログラムの向こう側に三次元映像が浮かび上がります．
これは，記録された微細なパターンによって生じた回折で照射された光が記録物体からの反射光相当の光となって観察者に飛んでくるためです．ちなみに，ホログラフィは，電子顕微鏡の解像度を向上させる技術として1948年D.Gaborにより考案されたものです．
この技術の難点としては
- 実際に撮影するための被写体が必要
- 撮影者の技術に再生像の質が大きく左右される
といったものがあります．
コンピュータホログラフィ
アナログホログラフィに対してこの技術では，3Dモデルのような仮想物体からの光(物体光波)を，角スペクトル法[1,2]のような伝搬計算手法を使用して計算機内で合成し，干渉縞データまでを計算したのちに，レーザーリソグラフィ装置などでガラス基板などをデータに基づいて彫ることでホログラムを作製します．
この手法では以下のような利点があります．
- 干渉縞(ホログラム)がデータであるため，複製や転送が容易
- 現実に存在しない物体のホログラムが作製可能
この成果物は「計算機合成ホログラム(CGH)」と呼ばれます．
また，あらゆる方向から観察しても立体感を感じられ，自然な再生像を生じるCGHを全方向視差CGHといいます．
#物体光波の計算
コンピュータホログラフィでは3Dモデルから回折してくる光を計算する必要があります．代表的なものとしては以下のようなものがあります．
- 点光源法
- ポリゴン法
- 光線サンプリング面(RS面)を用いる手法
コンピュータホログラフィで十分なサイズと視域を得るには莫大な解像度が必要であり，効率的な計算手法が必要です．
まず，点光源法ですが，この手法では仮想物体表面に点光源を充填し，各光源からの球面波の回折を計算したのちに，重畳することで物体光波を合成します．
この手法は，各点光源からの光を計算して最後に重畳すればよいだけなので，GPUを用いた並列計算に向いています．しかし，全方向視差CGHの計算では，点光源の数$\times$ホログラム面での標本点数の数だけ計算をする必要があります．そのため，計算量が膨大になりやすいという欠点があります．
ポリゴン法では，先ほどとは違い，仮想物体のポリゴンを面光源としてとらえ，各面光源からの回折波を計算し数値合成する手法です(3)．
面光源数は点光源数と比較して，圧倒的に少なくて済み，FFTを光波計算に使用できることから(角スペクトル法)，全方向視差CGHの計算時間が極めて短くなる利点を有します．
RS面を用いる手法(4, 5)についてですが，まずRS面とは物体から到来する光線を標本する平面であり，その標本点をRS点といいます．
RS点での光線情報に関しては，仮想物体ではCGのレンダリング，実在物体では複数視点からの写真撮影で得られる多視点画像から与えられます．
私が専門としてやってきたのはポリゴン法なので，それについて記していきます．
ポリゴン法の概要
一応簡単には述べましたが，もう少し詳細にポリゴン法について述べます．以下に用いる座標系を示します．
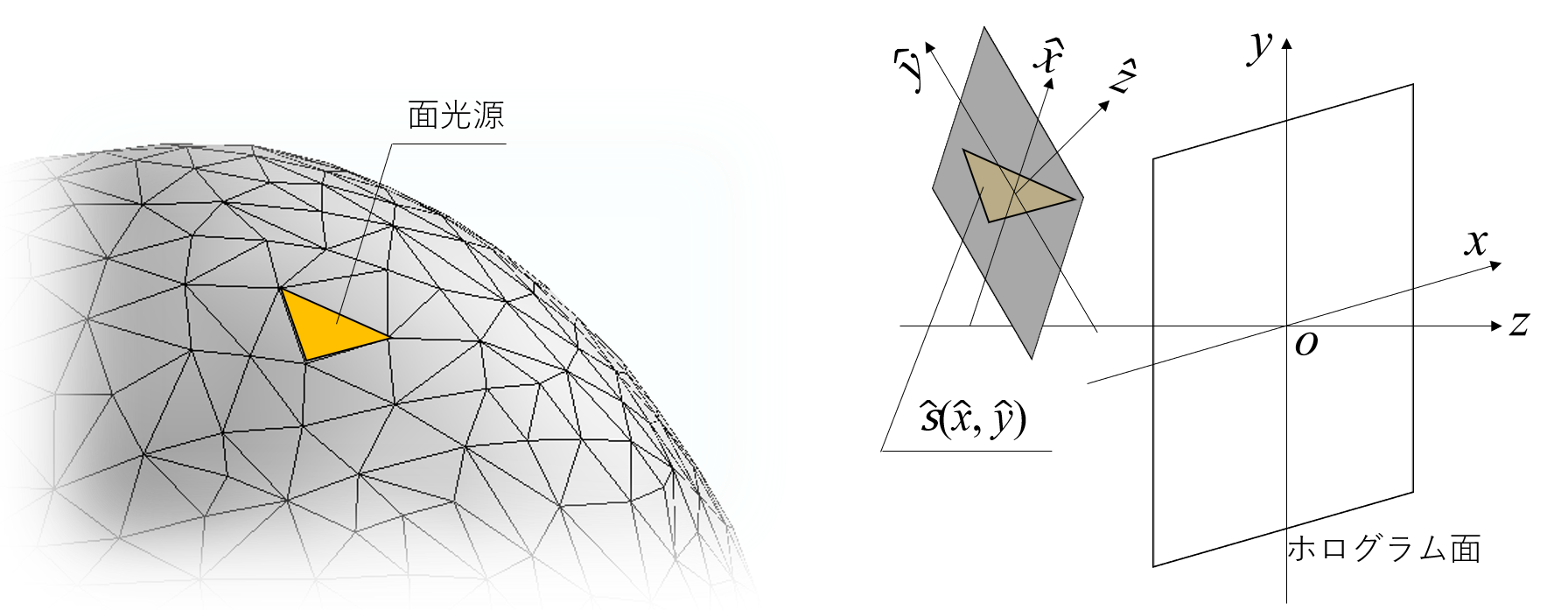
面光源は表面関数というものを用いて表されます．今，グローバル座標系$(x,y,z)$と各ポリゴンに用意されるローカル座標系$(\hat{x},\hat{y},\hat{z})$を考えます．この時，平面$(\hat{x},\hat{y};\hat{z}=0)$において表面関数$\hat{s}(\hat{x},\hat{y})$は
\hat{s}(\hat{x},\hat{y}) = \hat{a}(\hat{x},\hat{y})\exp[ik\hat{\phi}(\hat{x},\hat{y})]
と表されます．ここで，$\hat{a}(\hat{x},\hat{y})$はポリゴンの形状とテクスチャといった表面の材質などに関係する実関数であり，$\hat{\phi}(\hat{x},\hat{y})$は乱数位相です．これにより生じる光波を「ポリゴン光波」といいます．
ポリゴン法では各ポリゴンに対してこのようなポリゴン光波を発生させて物体光波を数値合成します．
乱数位相を使用しない場合は，光の進む方向がほぼ決まってしまい，広い範囲に光波が拡散しないので全方向視差CGHの計算ではこのような位相を使用します．以下に乱数位相を使用した場合としなかった場合の伝搬計算結果を示します．
このように，使用した光波は使用しなかった光波に対して，散乱していることがわかります．(メルセンヌツイスターで発生させた乱数を使用)
オクルージョン処理
オクルージョン処理はコンピュータホログラフィにおいて自然な再生像を得るために欠かせない重要な処理です．すごく簡単にですがこの処理をしないと以下のようになります(イメージということで)．
要するに，遮蔽されるべき部分が見えてしまうということです．
CGでいうところのデプスバッファを用いた隠面消去などに該当しますが，処理の内容が全く異なります．
CGではその視点からの隠面消去さえ行われていればよく，別の視点に移ったとしても逐次計算をすればよいです．
しかし，CGHでは計算をした後に再計算なんてできませんので，ホログラム作成の段階でデータが全方向の隠面消去情報を保持している必要があります．
ポリゴン法CGHでの隠面消去法には，主にシルエット法(6), と精密な隠面消去法(7)の二つがあります．簡単に解説はしますが是非とも論文を読むなり調べていただければと思います．
隠面消去法の概要
ここではポリゴン単位で遮蔽を行う手法である，ポリゴン単位シルエット法と精密な隠面消去法について記述していきます．
シルエット法は，そのポリゴンの背面に入射した光波を，ポリゴンのホログラム面に対する正射影形状のマスクで遮蔽します．この手法で実際に多くのCGHが計算・作製されています．
それとは異なり，ポリゴンの形状そのもので光波を遮蔽する手法が精密な隠面消去法です．
シルエット法では，そのマスクの形状の作り方と配置から，マスクの隙間を通過して漏洩する光波の成分が生じたり，露出したマスク自身が黒い影となって現れることがあります．特にこれは視点を大きく振ってホログラムを観察した場合に顕著にみられ，この手法の抱える問題となっています．反対に，精密な隠面消去法ではポリゴンの形状そのもので，ポリゴン後方からの光波を遮蔽するので，このような問題は生じません．以下は実際に計算してみた結果です．確かにシルエット法では表面にヒビが入っているように見え，精密な隠面消去法ではそれらが確認されません．
しかしここで疑問が生じます．そもそもなぜ後者の手法でオクルージョン処理をしていなかったのかという話です．後者の手法のほうが自然に感じられ，使用するのも当然であると考えられます．
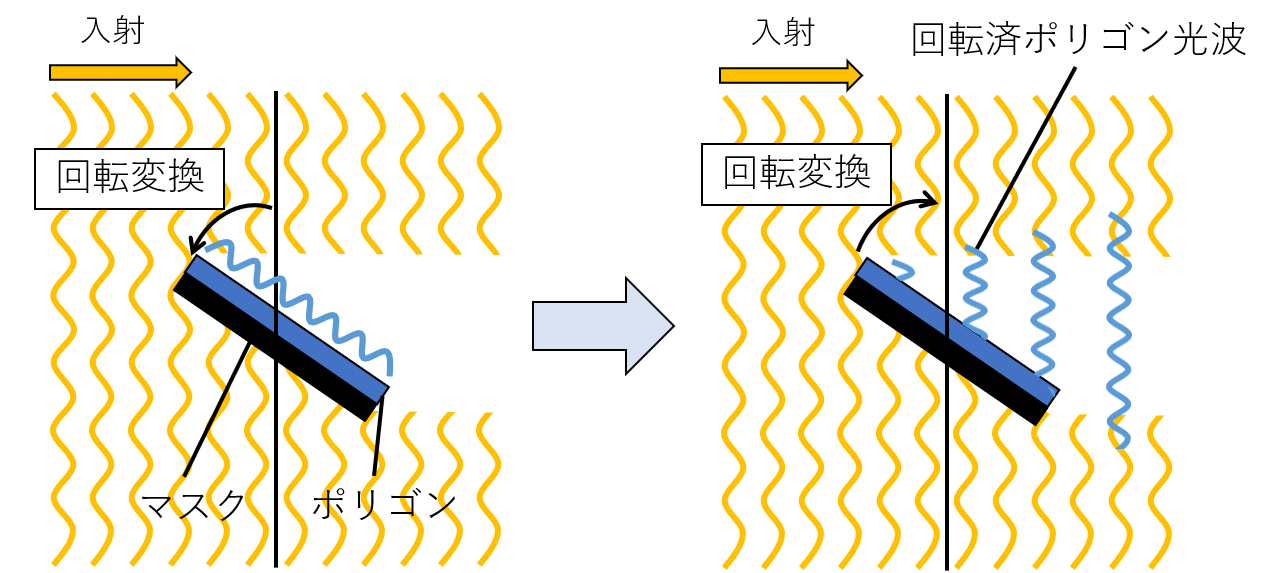
それは計算時間の問題です．シルエット法，精密な隠面消去法はともに前回説明した非平行平面間の伝搬計算手法である「光波の回転変換」を使用するのですが，前者は一回，後者は二回使用します．
また，後者は隠面消去を行う際に前者の使用する光波分布データよりも大きなデータサイズを扱うことになり，各ポリゴンに使用する光波の回転変換の計算量も多いです．そのため，精密な隠面消去法はポリゴン単位シルエット法と比較して計算時間が長大化します．
各手法における一ポリゴンあたりの処理
ここでは簡単に，ポリゴン単位シルエット法と精密な隠面消去法でどのような処理がなされて隠面消去(オクルージョン処理)が実現されているのかを見ていきましょう．
まずはポリゴン単位シルエット法からです．
箇条書きで書きます．
- ポリゴンの背面から入射してきた光波が，ホログラムと平行な平面で計算されている
- その光波分布にシルエットマスク形状のバイナリの分布(シルエット形状内部$=0$ 外部$=1$)を乗算する
- これにより背面から入射した光波はシルエットに沿って遮蔽されている
- ポリゴン面上で定義されているポリゴン光波を光波の回転変換の使用により，平行平面上で再構築する
- これにより計算された光波分布を，先ほどの遮蔽を受けた背景光波に加算する
以上により，ポリゴンのシルエット形状での遮蔽と，注目しているポリゴンからの光波が加味された光波分布を計算できます．以上をホログラム面から最も離れたポリゴンから手前のポリゴンに向かって順に行うことで，オクルージョン処理を施した物体光波が得られます．
そして精密な隠面消去法です．
同じく箇条書きで書きます．
- ポリゴンの背面から入射してきた光波が，ホログラムと平行な平面で計算されている
- その光波分布に光波の回転変換を使用することでポリゴン面上で再構築する
- 再構築された光波分布にポリゴン形状のバイナリの分布(ポリゴン形状内部$=0$ 外部$=1$)を乗算する
- これにより背面から入射した光波はポリゴンに沿って遮蔽されている
- この遮蔽済み光波に，ポリゴン面上で定義されているポリゴン光波を加算する
- 加算した結果に再度光波の回転変換を使用して，平行平面上で再構築する
以上により，ポリゴン形状での遮蔽と，注目しているポリゴンからの光波が加味された光波分布を計算できます．ポリゴン単位シルエット法と同様に，以上をホログラム面から最も離れたポリゴンから手前のポリゴンに向かって順に行うことで，オクルージョン処理を施した物体光波が得られます．
以上が各手法におけるオクルージョン処理になります．
オクルージョン処理の実際
ここまで書いてきた内容では，「マスク」を使用していました．しかし，このやり方では，各ポリゴンの光波計算に，ホログラム面サイズの大規模な光波分布を扱う必要があります．
これでは，計算時間の問題はおろか，メモリが足りないなんて問題も生じます．そのような問題を解決し，ポリゴン法CGHにオクルージョン処理を高速化するアルゴリズムとして「スイッチバック法」(8)が提案されています．この手法は，Babinetの原理に基づいて，マスクを使用する計算をその相補的な分布である開口を使用した計算に置き換え，計算に用いる光波を極めて小規模化し計算を高速化したものです．当初はポリゴン単位シルエット法に統合されていた手法ですが，精密な隠面消去法にも統合されました．是非とも論文をご覧ください．
以上のような計算手法により，高品質なCGHが計算・作製されています．光波の計算だけでなく，成果物である大容量の光波データを圧縮する技術や，鏡面反射を表面関数に取り込んで計算する技術など様々な魅力的な研究があります．ご興味持たれた方は，こちらも是非検索してみてください．
おわりに
ここまで読んでいただいた方，ありがとうございました．
この分野に興味の芽生えた方は是非ともOSA PublishingやSPIE DIGITAL LIBRARYなどで検索してみてください．きっと魅力的な論文・発表予稿に出会えるはずです．
今回はこれで終わりたいと思います．お疲れさまでした．