初めに
初めまして.今年の4月まで波動光学を専攻していた新社会人です.先日,角スペクトル法と周波数応答関数の帯域制限について記しました.
前
角スペクトル法は平行平面間の伝搬計算手法として大変優れており,長距離伝搬によって生じるエイリアシングもBand-Limited Angular Spectrum Method(原論文)によって大幅に軽減されました.実際に数値計算を行った結果も載せたので,その効果はわかっていただけたと思います.
さて,今回は前回の最後に示した「伝搬元の標本窓を縦横倍ずつにゼロパディングで拡張した後に伝搬計算を行い,その後元のサイズに縮小することで理想の結果を獲得できます」という根拠についてまず触れながら,平行平面間の伝搬計算手法の角スペクトル法を非平行平面間の伝搬計算手法に拡張した光波の回転変換という手法について述べていきます.
最初にこの記事を読んで計算できるであろう非平行平面間の伝搬計算の結果をgif画像で示しておきます.

4倍拡張角スペクトル法
これについては大変簡単です.ナイキスト定理を思い出してください.これは,最大周波数が$f_{\text{max}}$であるような信号を標本間隔$\Delta$で標本するときエイリアシングが起きないために以下を満足する必要があるというものでした.
2f_{\text{max}}\leq {\Delta}^{-1}\
数値伝搬計算を行う場合,メモリの消費を許すのであれば,この条件を常に満足することができます.
ある信号$f(x,y)$があり,$x,y$方向への標本間隔をそれぞれ$\Delta x, \Delta y$とし,さらに標本点数が$N_{x},N_{y}$であるとします.また,周波数空間での$u,v$方向への標本間隔をそれぞれ$\Delta u, \Delta v$とします.この時,標本間隔の関係式として以下が成り立ちます.これはDFTから得られます.
\Delta u= \frac{1}{N_{x} \Delta x}\;,\Delta v= \frac{1}{N_{y} \Delta y}
ここで信号の持つ最大周波数は分かってしまいます.各方向原点中心に分布していると考えると,$u,v$は以下を満たします.
|u|\leq \frac{N_{x}}{2}\Delta u=\frac{1}{2\Delta x}\;,|v|\leq \frac{N_{y}}{2}\Delta v=\frac{1}{2\Delta y}
つまり,周波数の限界は$u,v$方向それぞれ$\pm \frac{1}{2\Delta x}$と$\pm \frac{1}{2\Delta y}$です.(周波数にも正負があります)
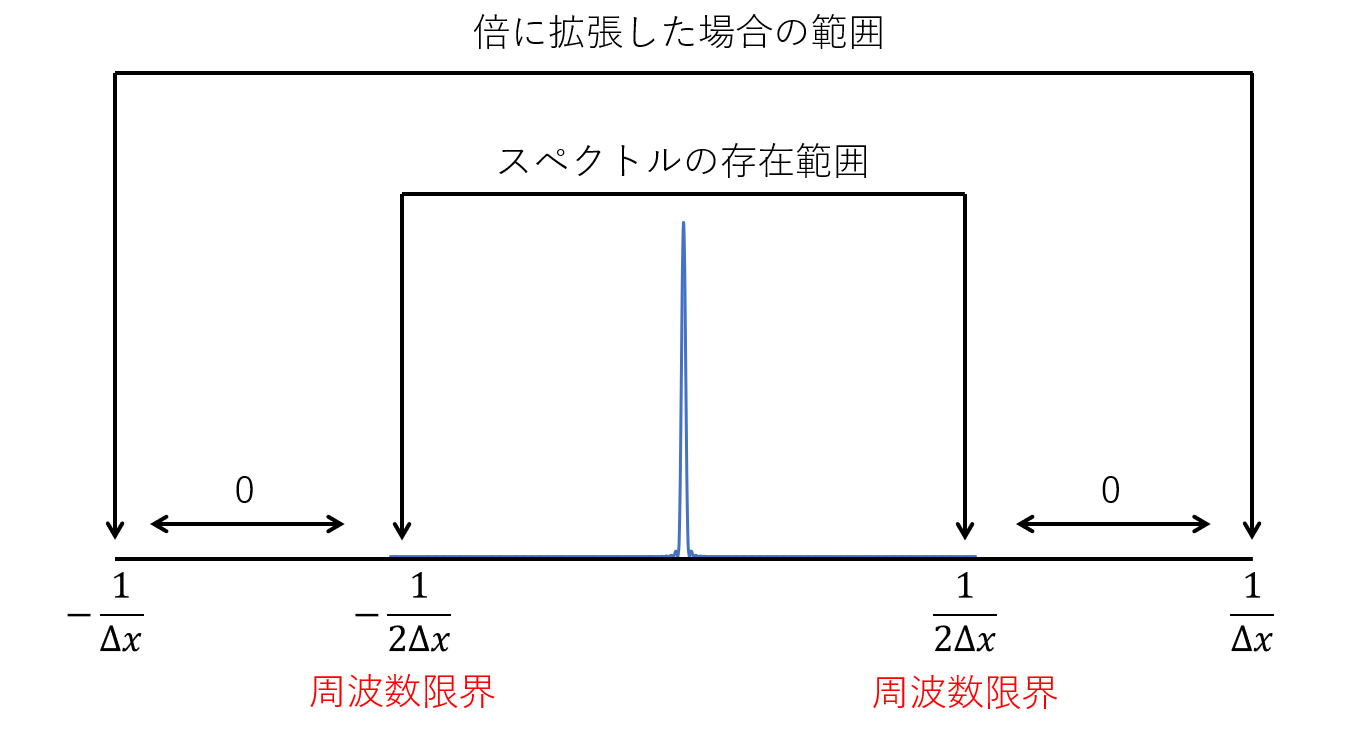
ここで,簡単のため一次元で考え,以下の図のように実空間でゼロ埋めにより標本窓の拡張を行った後に離散フーリエ変換で空間周波数スペクトルを計算した場合を考えます.
この時,ゼロ埋めの前後で信号の最大周波数は変化しません.しかし標本点数が$N_{x}\rightarrow 2N_{x}$になっています.つまり標本窓としての周波数の限界は$\pm \frac{1}{\Delta x}$のままですが,実空間での標本間隔は$\frac{\Delta x}{2}$です.(標本点数を倍にした時の実空間での標本間隔を$\Delta X$とすると,$\Delta X = \frac{1}{2N_{x}\Delta u} = \frac{1}{2}\frac{1}{N_{x}\Delta u}=\frac{1}{2}\Delta x$)
さて,この時,最大周波数の倍の値は$\pm \frac{2}{\Delta x}$であり,実空間の標本間隔の逆数(つまり標本周波数)は$\frac{2}{\Delta x}$となります.最大周波数の絶対値の2倍を標本周波数が超えていればナイキスト定理を満たしますから,この場合ギリギリではありますが満たしています.
従ってこの状態での角スペクトル法による伝搬計算ではエイリアシング誤差が出ません.
これが完全な計算結果を伝搬距離に全く関係なく得ることのできる方法です.しかし,メモリを縦横倍ずつの4倍消費するのでお使いのPCと相談しなければなりません.そういった意味でもBand-Limited Angular Spectrum Methodは有効です.
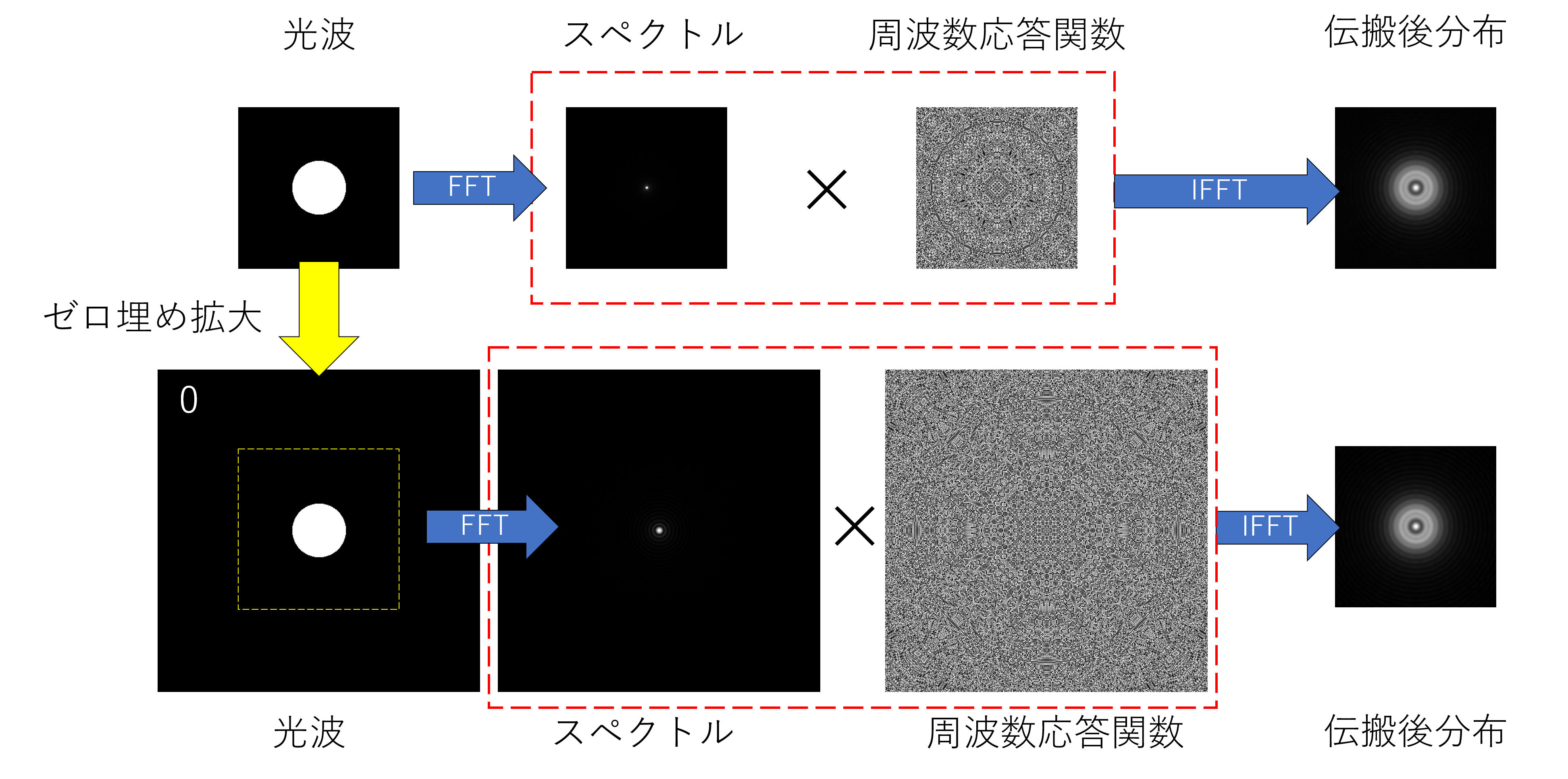
この伝搬計算についてまとめると以下のようになります.上の列が通常の角スペクトル法,下の列が4倍拡張角スペクトル法です.
非平行平面間の角スペクトル法(光波の回転変換)
通常の角スペクトル法は平行な二平面間の伝搬計算のみを扱うことができます.ただ,複数回使用してもよいのであれば非平行平面間の伝搬計算も扱えます.しかし,計算コストが高すぎるため向いていません.
ここでは,角スペクトル法を応用し,非平行平面間の伝搬計算に拡張した光波の回転変換(原論文)を紹介します.この手法は,計算機合成ホログラムにおける物体光波をポリゴン法を用いて数値合成する際に用いられている重要な伝搬計算手法です.
簡単にアルゴリズムの紹介
この手法のアルゴリズムは大きく分けて3段階です.
1.伝搬元の光波にFFTを使用して平面波の群に展開する
2.各平面波を伝搬先の平面へ座標回転する
3.座標変換された各平面波を逆FFTを使用することで結合し,光波を得る
角スペクトル法を元にしているのでやっていることは通常の角スペクトル法に似ています.要は,FFTを使用して伝搬したい光波を平面波の群に展開し,その各平面波をいじった後で逆FFTを使用し,所望の光波を得るのです.
ここではまず簡単にこの手順を追っていきます.
先ずは1ですね.これは前回でも書きましたが,光波にFFTを施すということは,様々な方向に回折する平面波の群に展開していることと等価でした.つまり図として表せば以下のようになります.
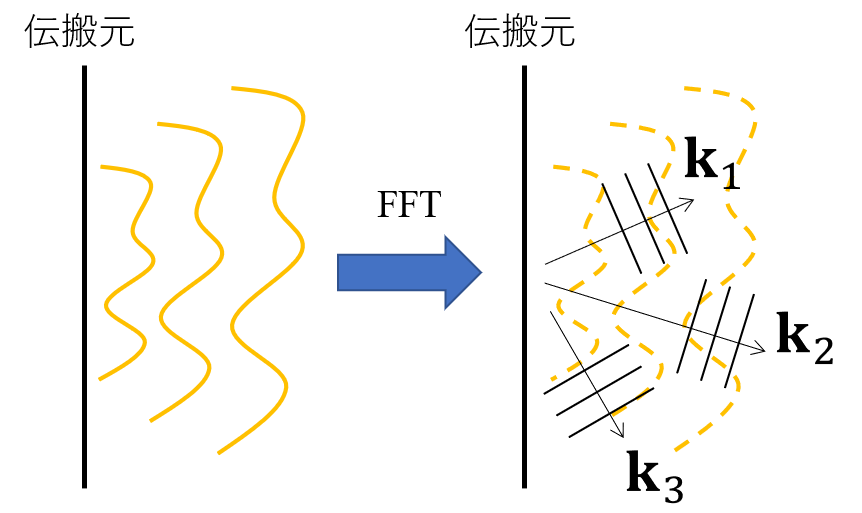
次に展開した各平面波に座用回転を施して座標変換をします.つまり,波動ベクトルを観測面で再解釈することにほかなりません.
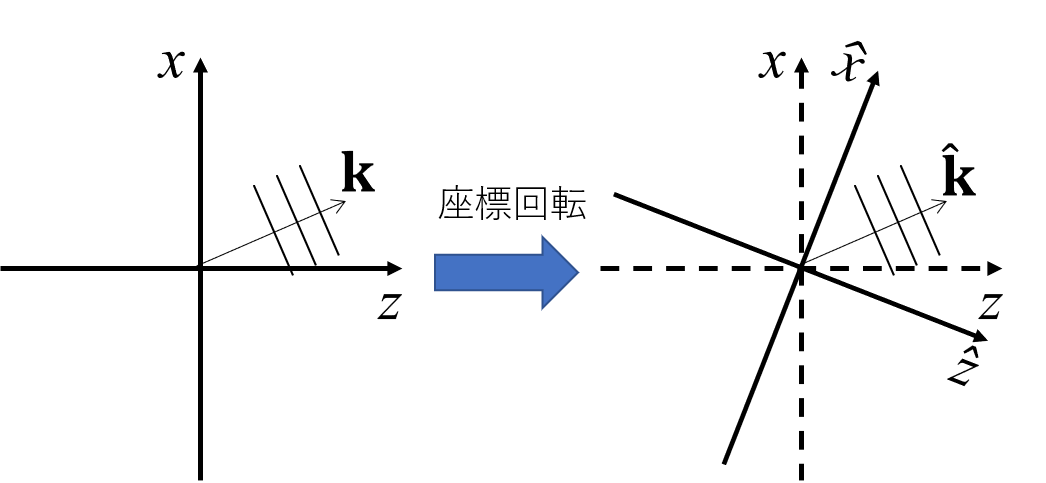
全ての平面波を座標変換した後は,逆FFTを使用して光波に戻せばよいです.これで元の光波は別の傾いた観測面上で再計算されます.
数式での紹介
ここでは前出のアルゴリズムを数式を用いて,かつ簡単に紹介していきます.ここでは以下の座標系を使用します.
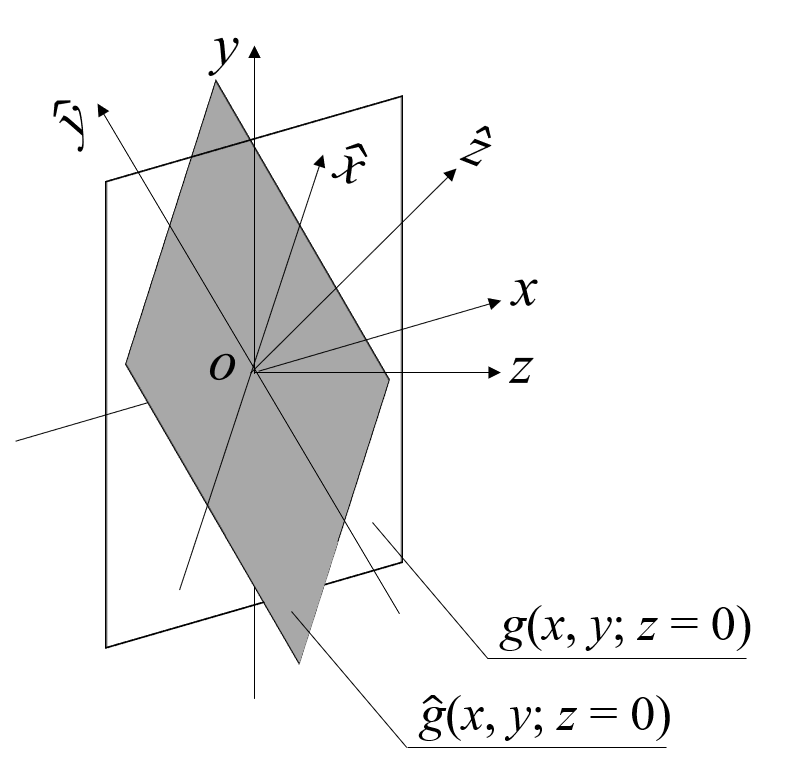
例のごとく,平面$(x,y,;z=0)$上の光波$g(x,y;z=0)$をフーリエ変換した結果$G(u,v;z=0)$の間には以下が成り立ちます.
G(u,v;z=0) = \iint g(x,y;z = 0)\exp[-i2\pi(ux+vy)]dxdy
g(x,y;z = 0) = \iint G(u,v;z=0)\exp[i2\pi(ux+vy)]dudv
そして,展開された各平面波の波動ベクトル$\mathbf{k}$は以下を満たします.
\mathbf{k}=(k_x,k_y,k_z)=2\pi(u,v,w(u,v))\\
|\mathbf{k}|={k_x}^{2}+{k_y}^{2}+{k_z}^{2}=2\pi/\lambda\\
w(u,v)=\sqrt{{\lambda}^{-2}-u^{2}-v^{2}}
伝搬先の光波$\hat{g}(\hat{x},\hat{y};\hat{z}=0)$についても同様のことが言えます.つまり,
\hat{G}(\hat{u},\hat{v};\hat{z}=0) = \iint \hat{g}(\hat{x},\hat{y};\hat{z} = 0)\exp[-i2\pi(\hat{u}\hat{x}+\hat{v}\hat{y})]d\hat{x}d\hat{y}\\
\hat{g}(\hat{x},\hat{y};\hat{z} = 0) = \iint \hat{G}(\hat{u},\hat{v};\hat{z}=0)\exp[i2\pi(\hat{u}\hat{x}+\hat{v}\hat{y})]d\hat{u}d\hat{v}\\
\mathbf{\hat{k}}=(\hat{k}_x,\hat{k}_y,\hat{k}_z)=2\pi(\hat{u},\hat{v},w(\hat{u},\hat{v}))
となります.次に,$\mathbf{R}$を$\mathbf{k}$から$\mathbf{\hat{k}}$への変換行列(直交行列)とします.従って
\mathbf{\hat{k}}=\mathbf{R}\mathbf{k},\;\mathbf{k}={\mathbf{R}}^{-1}\mathbf{\hat{k}}
となります.また,$\mathbf{R}$を次で定義しておきます.
\mathbf{R}=
\begin{pmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{pmatrix}
ここから,$(u,v,w(u,v))$と$(\hat{u},\hat{v},\hat{w}(\hat{u},\hat{v}))$について次が成り立つことがわかります.
u=\alpha (\hat{u},\hat{v})=r_{11}\hat{u}+r_{21}\hat{v}+r_{31}\hat{w}(\hat{u},\hat{v})\\,
v=\beta (\hat{u},\hat{v})=r_{12}\hat{u}+r_{22}\hat{v}+r_{32}\hat{w}(\hat{u},\hat{v})
従って,伝搬先のスペクトル$\hat{G}(\hat{u},\hat{v};\hat{z}=0)$は伝搬元のスペクトル$G(u,v;z=0)$を用いて
\hat{G}(\hat{u},\hat{v};\hat{z}=0)=G(\alpha (\hat{u},\hat{v}),\beta (\hat{u},\hat{v});z=0)
と書き直されます.
これで観測面におけるスペクトルは計算できたので,逆フーリエ変換で終わり!
と行きたいところですがもう少し待ってください.
$(u,v,w(u,v))$と$(\hat{u},\hat{v},\hat{w}(\hat{u},\hat{v}))$は非線形な変換によって写りあいます.そのような変換を伴う積分では,エネルギーを保存するために少し手間がいります.
伝搬元での平面波の全エネルギーを計算すると次のようになります.
E_{\text{source}} \propto \iint {|G(u,v;z=0)|}^{2}dxdy
次に,波動ベクトルの変換に関するヤコビアンを$|J(\hat{u},\hat{v})|$とすれば,伝搬先での平面波の全エネルギーは
E_{\text{reference}} \propto \iint {|\hat{G}(\hat{u},\hat{v};\hat{z}=0)|}^{2}|J(\hat{u},\hat{v})|dxdy
となりますから,スペクトル$\hat{G}(\hat{u},\hat{v};\hat{z}=0)$を光波$\hat{g}(\hat{x},\hat{y};\hat{z} = 0)$にするには,このヤコビアンを乗算してから逆フーリエ変換をすることになります.つまり,フーリエ変換の記号を$\mathcal{F}[\cdot]$としてこのアルゴリズムを定式化すると
\hat{g}(\hat{x},\hat{y};\hat{z} = 0) = \mathcal{F}^{-1}[\hat{G}(\hat{u},\hat{v};\hat{z}=0)|J(\hat{u},\hat{v})|]
となります.
実際の数値計算における結果
先ほどまでの理論はあくまでも数式の上だけの話です.実際に数値計算に落とし込むにはもう少しすることがあります.これに関しては,(より詳しい論文)に示されています.具体的に何をしないといけないかといいますとスペクトルの補間計算です.
スペクトルは波長の逆数を半径とするエワルド球面上に分布します.我々はこの球面上の標本窓の正射影を用いてスペクトルから光波を計算します.その時,座標回転をすると実際の標本点同士の間隔は変化しないのですが,正射影をとると大きくゆがんだ標本窓になります.
そこで,この手法ではまず,観測面のフーリエ空間に標本点の間隔が一定で矩形の標本窓を設定し,各点を伝搬元のフーリエ空間に逆写像し,近傍の標本点から補間計算をすることで所望のスペクトルを計算します.以下にコードを載せます.
こちら
void WaveFront::RotInFourierSpace(WaveFront& source, Interp interp, vec3* carrier)//フーリエ空間での回転
{
WaveFront& reference = *this;
mat3 rot = reference.GetRotMat(source.w_normal);
mat3 invrot = transpose(rot);//回転用の行列
double invL1 = 1 / w_lambda;
vec3 source0{ 0.0,0.0,(float)invL1 };
source0 = rot * source0;//キャリア周波数
int i, j;
for (j = 0; j < reference.w_ny; ++j)
{
for (i = 0; i < reference.w_nx; ++i)
{
//シフト座標系での周波数
vec3 ref = vec3{ static_cast<float>(reference.itox(i)),static_cast<float>(reference.jtoy(j)),static_cast<float>(invL1) };
//シフト座標系での周波数w成分
double w_ref = reference.GetWpow2(ref.getX(), ref.getY());
if (w_ref < 0)//エヴァネッセント領域は無視
{
reference.SetPixel(i, j, complex<double>(0.0, 0.0));
continue;
}
//観測面での周波数
vec3 shift = ref + source0;
//観測面での周波数w成分
double w_shift = reference.GetWpow2(shift.getX(), shift.getY());
if (w_shift < 0)//エヴァネッセント領域は無視
{
reference.SetPixel(i, j, complex<double>(0.0, 0.0));
continue;
}
shift.setZ(static_cast<float>(sqrt(w_shift)));
//伝搬元での周波数
vec3 sourcefreq = invrot * shift;
reference.SetPixel(i, j, source.GetInterpolatedValue(sourcefreq.getX(), sourcefreq.getY(), interp));
}
}
if (carrier != nullptr)
{
*carrier = source0;
}
}
void WaveFront::TiltedAsmProp(WaveFront& source, Interp interp, vec3* carrier)
{
WaveFront& reference = *this;
source.fft2D(-1);
reference.pitchtrans();//標本間隔の変換
reference.RotInFourierSpace(source, interp, carrier);//光波の回転変換
reference.fft2D(1);
reference /= GetN();
}
TiltedAsmPropを呼び,中でRotInFourierSpaceを使用することでスペクトルを回転しています.シフト座標系というのは説明にありませんでしたが,先ほどの論文に書いています.この座標系の導入により,FFTの標本窓を小さくして計算の高速化を図ることができます.
早速計算してみます.
伝搬元の開口のパラメタは前回と同じく縦横512ピクセル,標本間隔1[μm],波長は630[nm]で設定します.

そもそもこれは光波というより穴なので,少し角スペクトル法で伝搬してみます.
1[mm]伝搬してみると

です.これも前回載せましたね.これを$y$軸中心40°回転した座標系で観測した結果は

となり,60°回転した座標系で観測した結果は

となります.
また,この状態から更に$x$軸周りに30°回転した座標系での観測結果は

となります.今回は補間計算にBi-cubic補間を使用しています.計算時間は17[ms]程度(FFT:15[ms] 補間:2[ms])です.
このように精度良く計算できていることがわかります.
最後に,y軸周り30°固定で,x軸周りに徐々に回転した場合の計算結果をgifで示しておきます.

おわりに
今回はここまでです.光波の回転変換を制する者はポリゴン法CGHを制するといっても過言ではない極めて重要な伝搬計算手法です.勿論,点光源法や波面変換などを用いる場合は使うことはないですが(たしかそうです),基本的な非平行な伝搬計算を精度良くかつ高速に計算できる手法なので,是非ともものにしていただければと思います.
次は計算機合成ホログラム(CGH)の物体光波生成手法についての記事を書こうと思います.
ではこれにて失礼します.お疲れさまでした.
次