TL; DR
- Group Lassoを使えば説明変数をグループ単位で選択してくれる
- Group Lassoの理論や最適化手法を簡単にまとめた
- pythonでGroup Lassoの学習を行えるsklearnライクなパッケージを作ってみた
はじめに
Group Lasso (Yuan et al., 2005) は、説明変数間でグループを形成しているときに、変数選択において、(個々の説明変数を選ぶのではなく、)グループ単位で選択したいときに利用する方法です。
この手法について理論と実践を統合してまとめている記事がなかなか見当たらなかったので、まとめてみました。
また、Group Lassoを実行できるpythonパッケージがあまり充実していなかったので自作しました。そのパッケージの紹介です。
なお、今回は「説明変数においてグループの重複がないケース」のGroup Lassoに限定して説明を行います。
理論の概要
目的関数
以降、Group Lassoのモデルのパラメータ、すなわち偏回帰係数を${\boldsymbol x} \in \mathbb{ R }^{M}$とします。
Group Lassoの目的関数$F({\boldsymbol x})$ は、
- 損失関数を$f({\boldsymbol x})$
- 正則化パラメータを$\lambda$
とすると、以下のようになります。
F({\boldsymbol x}) = f({\boldsymbol x}) + \lambda \sum_{j=1}^{J} ||{\boldsymbol x}_{G_{j}}||
ただし、$G_j$は、$j$番目のグループに属する変数の集合を表しており、
{\boldsymbol x}_{G{j}} \in \mathbb{ R }^{m_{j}} \,\,\, \left(\sum_{j=1}^{J}m_{j} = M \right)
です。
また、$||{\boldsymbol x}||$は、ベクトル${\boldsymbol x}$のL2-normを表します。
どうしてこの目的関数を最適化するとグループ単位で落ちてくれるか、については、こちらが図を踏まえて大変わかりやすく説明してくれています。
パラメータの更新
以下の方法でパラメータ${\boldsymbol x} \in \mathbb{ R }^{M} $を更新していきます。

つまり、まず正則化項を無視して$f({\boldsymbol x})$のみに対して最急降下法を行い、その結果得られた$\tilde{{\boldsymbol x}}$に対して、グループごとに上記2.2.のようなアップデートを行います。
上記の式の導出の過程を追いたい場合には、下記の「もっと詳しく」を参照してください。
実践
Group Lassoをpythonで使えるパッケージがあまり充実していなかったため自作しました。リポジトリは以下です。
パッケージインストール
インストール方法は以下のとおりです。
$ git clone https://github.com/AnchorBlues/GroupLasso.git
$ cd GroupLasso
$ python setup.py install
モジュール名はgrouplasso、モデルのクラスの詳細は以下のとおりです。
| クラス名 | 手法 | 損失関数 |
|---|---|---|
| GroupLassoRegressor | 回帰 | 二乗和誤差関数 (つまり線形回帰) |
| GroupLassoClassifier | 分類 (※ 2クラス分類のみサポート) |
交差エントロピー誤差関数 (つまりロジスティック回帰) |
以下のようにするとimportできます。
from grouplasso import GroupLassoRegressor, GroupLassoClassifier
チュートリアル
sklearnのボストンデータのデータを利用します。
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
data = load_boston()
# 学習の効率化のため、各説明変数は正規化する
x = StandardScaler().fit_transform(data.data)
y = data.target
変数ごとにグループを指定してやる必要がある。
各変数に対して、グループ番号を以下のようにしました。
| 変数名 | グループ番号 |
|---|---|
| CRIM | 0 |
| ZN | 1 |
| INDUS | 1 |
| CHAS | 2 |
| NOX | 2 |
| RM | 3 |
| AGE | 3 |
| DIS | 3 |
| RAD | 4 |
| TAX | 4 |
| PTRATIO | 5 |
| B | 6 |
| LSTAT | 6 |
グループ番号が同じ変数を同じグループとみなします(※ 上記のグループの分け方は割と適当です)。
上記に対応するように、グループidを指定するための変数を作成してやります。
group_ids = np.array([0, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 6, 6])
モデルを作成して、学習のための設定を行います。
alpha = 1.0 # 正則化パラメータ
eta = 0.2 # 学習率
model = GroupLassoRegressor(group_ids=group_ids, random_state=42, alpha=alpha, verbose=False, eta=eta)
# モデルの学習
model.fit(x, y)
# モデルの偏回帰係数を出力
print(model.coef_)
各説明変数のグループ番号、及び偏回帰係数の値は以下の通りとなりました。
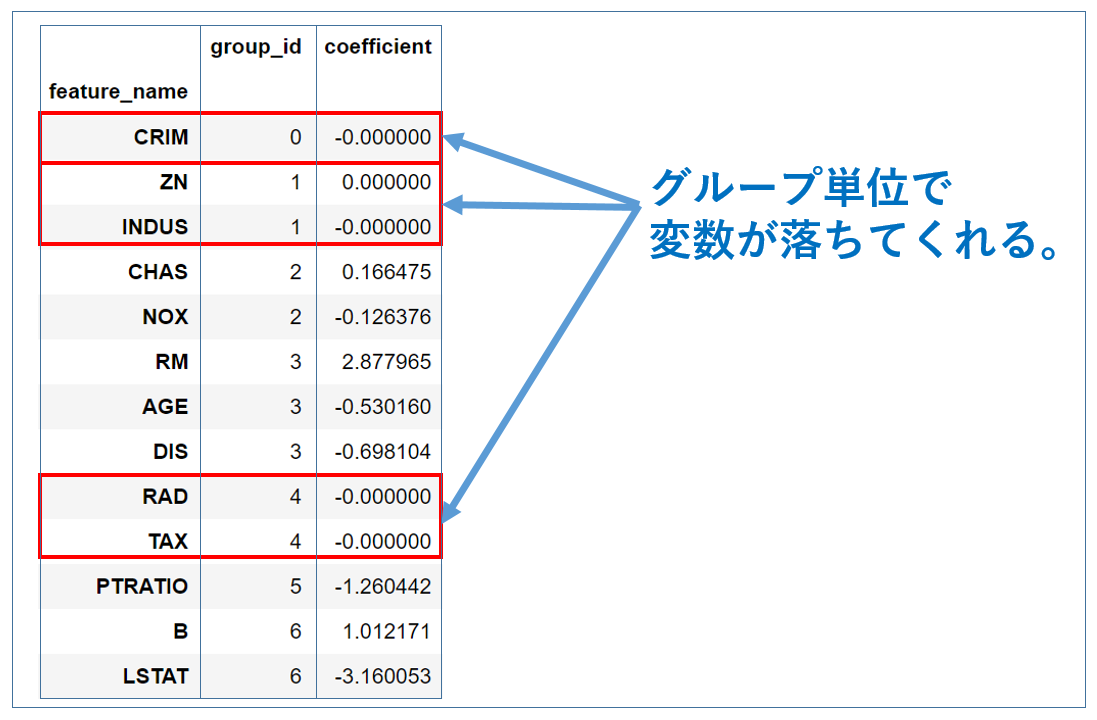
グループ0, 1, 4に属する変数の偏回帰係数は全て0となった一方で、それ以外のグループに属する変数は全て「0でない」値となりました。
このように、Group Lassoを用いると、グループ単位で
- 全ての偏回帰係数が0
- 全ての偏回帰係数が「0以外」
にきれいに分かれてくれます。
mnistに対する結果
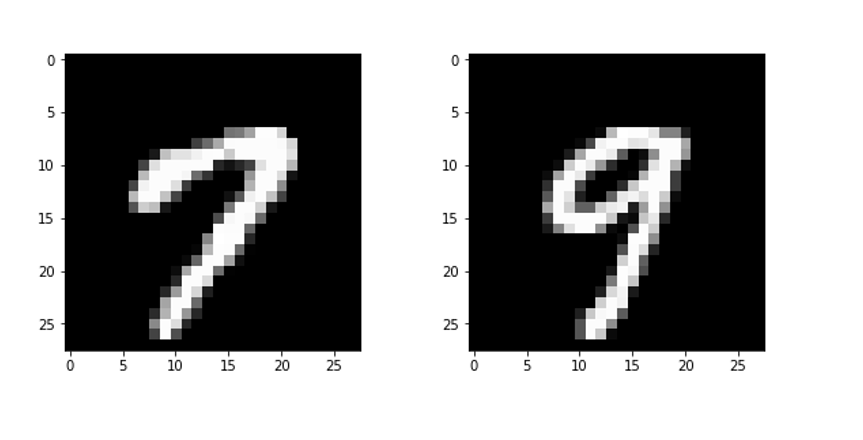
mnistデータから、正解ラベルが「7」と「9」のインスタンスのみを取り出し、この2つの文字を識別するモデルをGroupLassoClassifierを用いて学習しました。
ここでは、学習のスクリプトは割愛して、結果だけを掲載します。
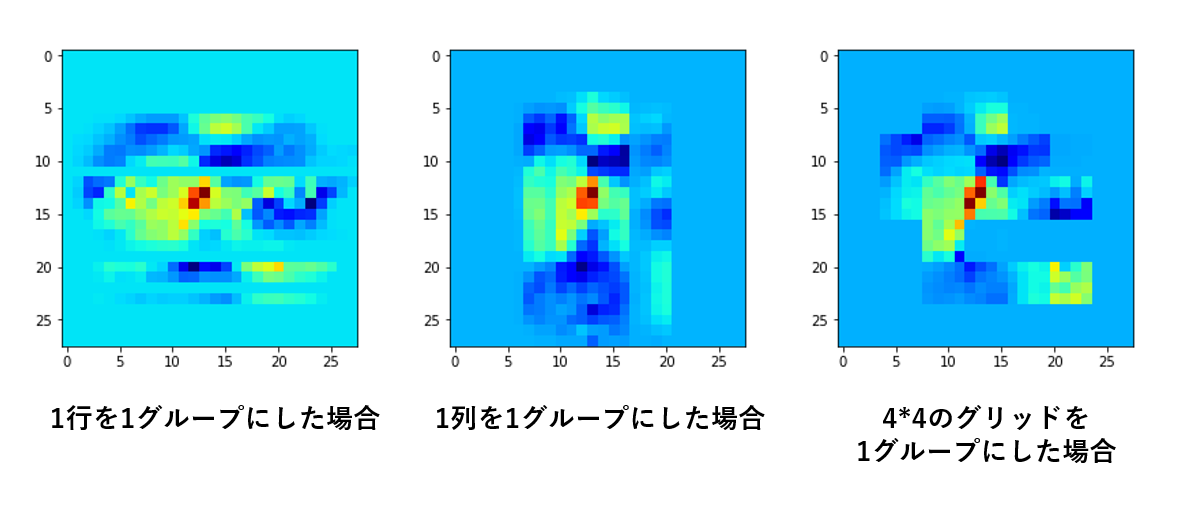
偏回帰係数を28*28に変形してマップした結果はそれぞれ以下の通りとなりました。
左は行単位、真ん中は列単位、右は粗いグリッド単位で説明変数が落ちてくれていることが分かります。
同じGroup Lassoでも、グループのとり方を変えるだけで落ちるピクセルが大きく異なる、という面白い結果となりました。
もっと詳しく
Group Lassoのパラメータの更新に関しての詳細です。
Group Lassoの目的関数は、微分不可能な点があるため、最適化に通常の最急降下法を用いることができません。
しかし、$f({\boldsymbol x})$を線形近似してやることにより、局所的に$F({\boldsymbol x})$を最小にする${\boldsymbol x}$を求めることは可能になります。Lassoをこのように線形近似で解くときに用いる手法を近接勾配法といいます。
近接勾配法についてはこちらが詳しいですが、左記の記事ではGroup LassoのProximal Operatorの式の導出が掲載されていなかったので、ここで「Group LassoにおけるProximal Operatorの式の導出」を行ってみます。
目的関数が
F({\boldsymbol x}) = f({\boldsymbol x}) + g({\boldsymbol x}) \tag{1}
とすると、近接勾配法による更新式は、
{\boldsymbol x}_{k+1} = {\rm prox}_{\eta g}\left( {\boldsymbol x}_{k} - \eta \nabla f\left( {\boldsymbol x}_{k}\right)\right) \tag{2}
です。この式を、近接写像${\rm prox}$の定義に従って式変形すると、以下の通りになります。
{\boldsymbol x}_{k+1} = {\rm argmin}_{{\boldsymbol x}} \left( \nabla f({\boldsymbol x}_{k})^{T}\left( {\boldsymbol x} - {\boldsymbol x}_{k}\right) + \frac{1}{2 \eta} ||{\boldsymbol x} - {\boldsymbol x}_{k}||^{2} + g({\boldsymbol x})\right) \tag{3}
つまり、
h({\boldsymbol x}) = \nabla f({\boldsymbol x}_{k})^{T}\left( {\boldsymbol x} - {\boldsymbol x}_{k}\right) + \frac{1}{2 \eta} ||{\boldsymbol x} - {\boldsymbol x}_{k}||^{2} + g({\boldsymbol x}) \tag{4}
とおくと、$h({\boldsymbol x})$を最小にする${\boldsymbol x}$が${\boldsymbol x}_{k+1}$ということになります。
ここで
g({\boldsymbol x}) = \lambda \sum_{j=1}^{J} ||{\boldsymbol x}_{G_{j}}|| \tag{5}
とし、(5)を(4)に代入して$h({\boldsymbol x})$を${\boldsymbol x}$で微分すると、以下の通りとなります。
\frac{\partial h({\boldsymbol x})}{\partial {\boldsymbol x}} = \nabla f({\boldsymbol x}_{k}) + \frac{1}{\eta} \left( {\boldsymbol x} - {\boldsymbol x}_{k}\right) + \lambda \frac{\partial}{\partial {\boldsymbol x}} \sum_{j=1}^{J} ||{\boldsymbol x}_{G_{j}}|| \tag{6}
このままだと正則化項の部分がバラせないので、${\boldsymbol x}$の$i$番目の要素$x_i$に着目します。
今、要素$x_i$が$j$番目のグループに属しているとすると、
\begin{eqnarray}
\frac{\partial h({\boldsymbol x})}{\partial x_i} &=& \nabla f({\boldsymbol x}_{k})_i + \frac{1}{\eta} \left( x_i - x_{ki}\right) + \lambda \frac{\partial}{\partial x_i} ||{\boldsymbol x}_{G_{j}}|| \\
&=& \nabla f({\boldsymbol x}_{k})_{i} + \frac{1}{\eta} \left( x_{i} - x_{ki}\right) + \lambda \frac{x_{i}}{||{\boldsymbol x}_{G_{j}}||}
\end{eqnarray} \tag{7}
すなわち、$\frac{\partial h({\boldsymbol x})}{\partial x_{i}} = 0$を解くと、
x_{i} = x_{ki} - \eta\nabla f({\boldsymbol x}_{k})_{i} - \eta \lambda \frac{x_{i}}{||{\boldsymbol x}_{G_{j}}||} \tag{8}
この$x_i$が、「$h({\boldsymbol x})$を最小にする${\boldsymbol x}$」の$i$番目の要素です(※ 式の両辺に$x_i$が含まれることに注意してください)。
ここで、わかりやすさのため、
\tilde{{\boldsymbol x}}_{k} := {\boldsymbol x}_{k} - \eta \nabla f({\boldsymbol x}_{k}) \tag{9}
のように$\tilde{{\boldsymbol x}}$を定義すると、式(8)は、
x_{i} = \tilde{x}_{ki} - \eta \lambda \frac{x_{i}}{||{\boldsymbol x}_{G_{j}}||} \tag{10}
となります。
式(10)を見ると、同じグループ$G_j$に属する要素$i$に対する更新式は、以下のように一括りにすることができることがわかります。
{\boldsymbol x}_{G{j}} = \tilde{{\boldsymbol x}}_{k, G_{j}} - \eta \lambda \frac{{\boldsymbol x}_{G{j}}}{||{\boldsymbol x}_{G_{j}}||} \tag{11}
以後の目標は、この式を${{\boldsymbol x}}_{G_j}$について解くことです。
式(11)を見ると、${{\boldsymbol x}}_{G_j}$ はスカラー$\alpha$を用いて以下のような形で表せることがわかります。
{\boldsymbol x}_{G{j}} = \alpha \tilde{{\boldsymbol x}}_{k, G_{j}} \tag{12}
(11)を(12)に代入し、両辺の係数のみを取り出して式変形すると、
\alpha \left( 1 + \frac{\eta \lambda}{|\alpha|\,||\tilde{{\boldsymbol x}}_{k, G_{j}}||}\right) = 1
\Leftrightarrow \alpha \left( |\alpha|\,||\tilde{{\boldsymbol x}}_{k, G_{j}}|| + \eta \lambda \right) = |\alpha|\,||\tilde{{\boldsymbol x}}_{k, G_{j}}|| \tag{13}
今、$\eta$, $\lambda$はいずれも正であることから、式(13)の括弧の中身は正。よって$\alpha$も正であることがわかります。
そこで$|\alpha| = \alpha$として式(13)を$\alpha$について解くと、
\alpha = 1 - \frac{\eta \lambda}{||\tilde{{\boldsymbol x}}_{G_{j}}||} \tag{14}
今、$\alpha$は正なので、
\alpha = \max\left( 0, 1 - \frac{\eta \lambda}{||\tilde{{\boldsymbol x}}_{G_{j}}||}\right) \tag{15}
これを式(12)に代入することにより、
{\boldsymbol x}_{G{j}} = \max\left( 0, 1 - \frac{\eta \lambda}{||\tilde{{\boldsymbol x}}_{G_{j}}||}\right) \tilde{{\boldsymbol x}}_{k, G_{j}} \tag{16}
となります。
この$x_{G_j}(j=1,...,J)$が、$h({\boldsymbol x})$を最小にする${\boldsymbol x}$(の構成要素)、すなわち${\boldsymbol x}_{k+1}$(の構成要素)ということになります。