こんばんは(;´・ω・)
前回、ここ で最後に DP に触れてみましたが、
今一 ピンと来なかったので、もうちょっとカジってみます(*´з`)9
初心者なので、早速ググってみると
"分からない"、
"壁"、
"登竜門"
とか色々、一緒に出てきました。
やっぱり皆、一度はハマるんですね。
取りあえず、やってみましょう。
初級問題:与えられた要素を任意に組み合わせて最大値を求めてみます。
N = 3 # 要素数
A = [7,-6,9] #要素
memo = [0]*(N+1) # 要素数 + 1 のメモを 1 行(all 0)を用意
for i in range(N):
memo[i+1]=max(memo[i],memo[i]+A[i])
print(memo[N])#回答の表示
for 文は何をしているのでしょうか?
一個ずつ追って見ましょう。
i = 0 のとき
memo[0] には 0 が格納されていますが、
memo[0] + A[0] = 0 + 7 と比べると何方が大きいでしょうか?
勿論、後者ですよね。
計算結果は memo[1] に 7 を格納します。

i = 1 のとき
memo[1] にある 7 と
memo[1]+A[1] の 1 とでは、どちらが大きいでしょうか?
前者ですよね?
この結果は memo[2] に格納します。

i = 2 のとき
memo[2] にある 7 と
memo[2] + A[2] の 16 はどちらが大きいですか?
はい、結果を格納します。

最後に memo[3] を表示すれば回答にたどり着けます。
御覧の通り、計算結果を次のセルに渡すので、最終的には
計算したい要素数 + 1 のメモが必要です。
個人的には、以下のような書き方もあると思います。
N = 3
A = [7,-6,9]
memo = [0]*(N)
memo[0] = A[0]
for i in range(1,N,1):
memo[i]=max(memo[i-1],memo[i-1]+A[i])
print(memo[N-1])
上記は memo[0] に初期値を入れて、
for 文をmemo[1]から始めています。
こうすることで、ひとつ前の値(= i-1)を参考に、
今の値(= i ) を算出することが出来ます。
へー( ゚Д゚)
っとなったところでググって次なる問題を探した所、
こちらに出会いました。
分かり易くて感謝のコメントを思わず捧げてしまいました。
早速、カエル問題にチャレンジしました。
a = [2,9,4,5,1,6,10]
N = len(a)
memo = [0]*(N)
for i in range(1,N,1):
memo[i]=memo[i-1]+abs(a[i-1]-a[i])
if i > 1 :
memo[i] = min(memo[i],memo[i-2]+abs(a[i-2]-a[i]))
print(memo[N-1])
有識者の皆様は初期化する意味で、INF を全セルに代入し、
+1 で移動するときのコストと比較して小さい方を上書き。
そのあとに +2 で移動するときのコストを比較して、
小さければ上書きし最終セルを出力されています。
個人的には、All 0 初期値とし、
+1 のコストをいきなり上書きしても問題ないと思います。
なぜなら、最初に必ず+1 で移動した場合のコストを埋めてから、
+2 の移動コストと比較しないと問題が解けないからです(笑)
もう一つの書き方も試しました。
a = [2,9,4,5,1,6,10]
N = len(a)
memo = [0]*(N)
for i in range(N-1):
memo[i+1]=memo[i]+abs(a[i+1]-a[i])
if i >= 1 :
memo[i+1] = min(memo[i+1],memo[i-1]+abs(a[i+1]-a[i-1]))
print(memo[N-1])
私は冒頭にあるメモの概念と、
以下のアプローチをイメージ出来たら理解した気分になれました(笑)
Step 1. +1 のコストを最初に memo
Step 2. +2 のコストと Step 1 で求めた memo を比較して小さい方の値を上書き
まだまだ、足を踏み入れたばかりなので、
もう少し違う問題も挑戦しようと思います。
11/26 update
例えば、+1 , +2 でカエルが跳んだ場合の MIN コストを求めていましたが、
飛ばす柱の数を K と定義されたらどうしますか?
問題によりますが、K まで 1 ずつインクリメントして
全てのケースを比較して、MIN コストを求めるとすると、どうでしょう。
例として 1 飛ばしと 2 飛ばしを書いてみました。
K = [1,2]
a = [2,9,4,5,1,6,10]
N = len(a)
memo = [0] * (N)
for i in range(1,N,1):
memo[i] = memo[i-1]+abs(a[i]-a[i-1])
for k in K:
if i > k:
memo[i] = min(memo[i],memo[i-(k+1)]+abs(a[i]-a[i-(k+1)]))
print(memo[N])
各ポイントに着地するときに、隣にジャンプ or +1 or +2 を三択して
最小値を求めてから次に向かうことで Goal に辿り着くときには最小値を求められる算段です。
下の図は、プログラムが最小を選びながら進んでいるイメージをまとめたものです。
もっと分かり易くできると思うんですけど、すいません、センスがない m(_ _)m
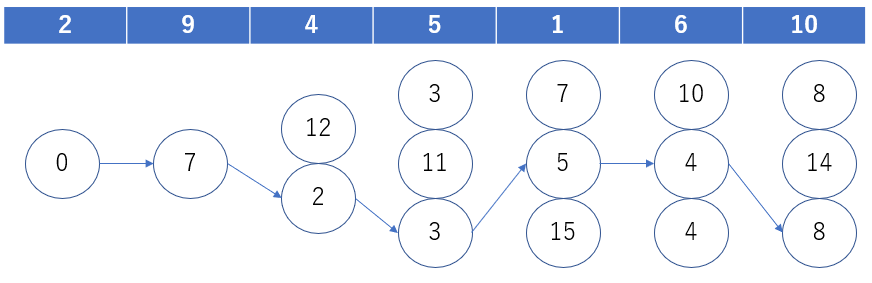
配る DP 行きましょう。
K = [1,2]
a = [2,9,4,5,1,6,10]
N = len(a)
memo = [0] * (N)
for i in range(N-1):
memo[i+1] = memo[i]+abs(a[i+1]-a[i])
for k in K:
if i >= k:
memo[i+1] = min(memo[i+1],memo[i-k]+abs(a[i+1]-a[i-k]))
print(memo[N-1])
DP の事だけ考えると、
他のこと忘れますね(笑)
11/27 update
昨日のイメージをもう少し補足してみます。
memo[0],memo[1]までは良いと思いますが、memo[2]からが本番です。
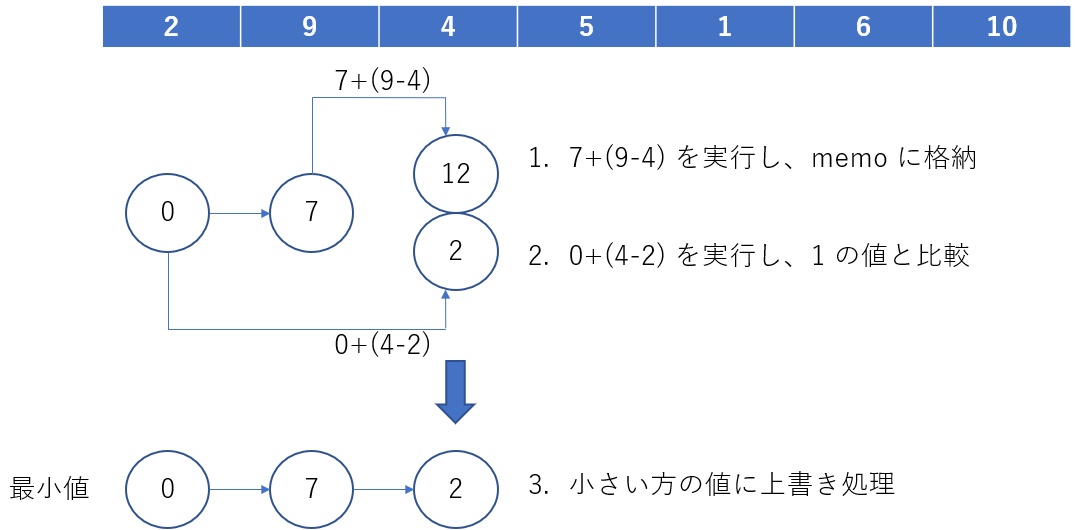
最小値 2 を探し出しました。
次の memo[3] は memo[0] - memo[2] の 3 つ中から最適値を見つけます。

残りの作業は同じ内容なので補足説明は省きます。

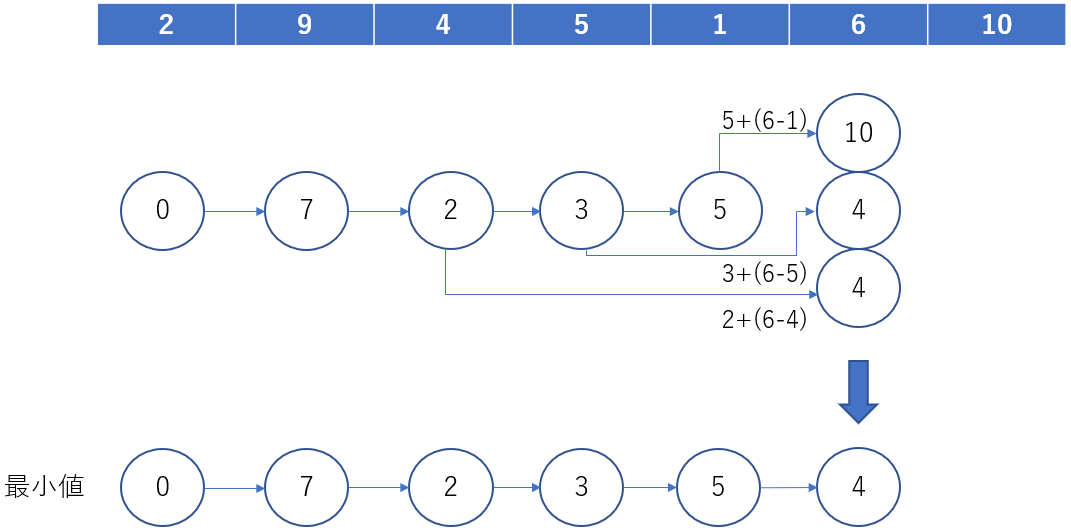
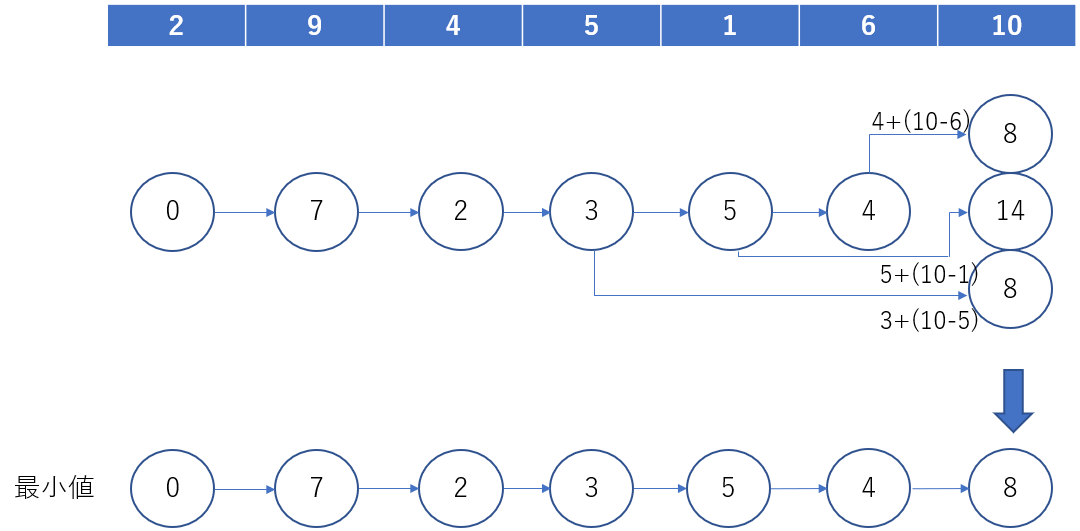
行ってみたいなー、幸福の国。。
っというわけで、以下の問題にも挑戦しました。
勿論、問題はここを参照にしています
---------------------------------------------------------------------------
N 日間の夏休みです。i 日目には、
A: 海で泳ぐ。幸福度 ai を加算
B: 山で虫取りする。幸福度 bi を加算
C: 家で宿題をする。幸福度 ci を加算
の三択の中から好きなものを選ぶことができます。ただし、2 日連続で A, B, C のうちの同一種類の活動を選択をすることはできません。この制約下で最終的に得られる幸福度の総和を最大にせよ。
---------------------------------------------------------------------------
0日目は幸福度は 0 らしいので、初日に A[0] = A, A[1] = B , A[2] = C と
アクティビティを行う 3 パターンの start が想定されます。
このように考えると、アクティビティは日を追うごとに複雑になるので、
前述にあるようにメモが 1 行だけでは追い付かなくなります。
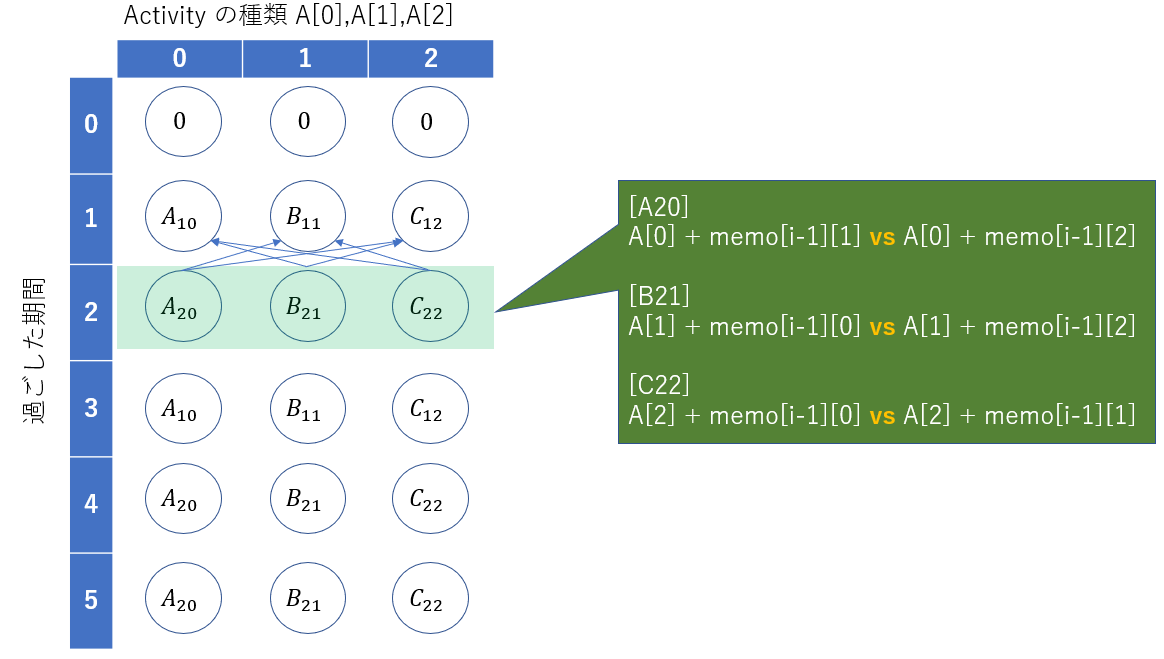
上図は貰う DP で考えています。
勿論、2 日目の幸福度を求めるためには前日の情報が必要です。
考慮と言っても、幸福度が高くなる経路が何方かだったかを
確認してメモできれば OK です。
# fortune point
A = [0,1,3]
# kind of activity
K = 3
# total days
D = 10
ANS = 0
# memo table
memo = [[0 for l in range(len(A))] for m in range(D)]
# First day
memo[1][0] = A[0]
memo[1][1] = A[1]
memo[1][2] = A[2]
for i in range(2,D,1): # Day
for j in range(K): # Activity
for k in range(K):# Other Activity
if j == k:
continue
memo[i][j]=max(A[j],A[j]+memo[i-1][k])
# list the point during period
for m in range(D):
print(f"{m}th day is {memo[m]}")
for n in range(K):
ANS = max(ANS,memo[9][n])
print(ANS)
0th day is [0, 0, 0]
1th day is [0, 1, 3]
2th day is [3, 4, 4]
3th day is [4, 5, 7]
4th day is [7, 8, 8]
5th day is [8, 9, 11]
6th day is [11, 12, 12]
7th day is [12, 13, 15]
8th day is [15, 16, 16]
9th day is [16, 17, 19]
19
しっかりとしたイメージを作れば何とか書けますね。
お疲れ様でした ^^) _旦~~
12/02 update
新しい問題にチャレンジしてみました。
こちらです。
はじめ、高橋君の満腹度は H です。N 日間のそれぞれの日について、その日にとる食事を次の 3 種類の中から 1 つ選びます。
・普通の食事: A 円の出費をして、満腹度が B 増える。
・質素な食事: C 円の出費をして、満腹度が D 増える。(ただし、C<A かつ D<B)
・食事抜き: 出費なしで、満腹度が E 減る。
厳しく節約すれば出費を抑えることができますが、あまりに節約しすぎて体調を崩してしまってはいけないため、
N 日間で一度も満腹度が 0 以下にならないようにしなければなりません。
高橋君は最低何円の食費で N 日間を乗り切ることができるでしょうか?
今まで通りの考え方だとハマります。
なぜなら。。。
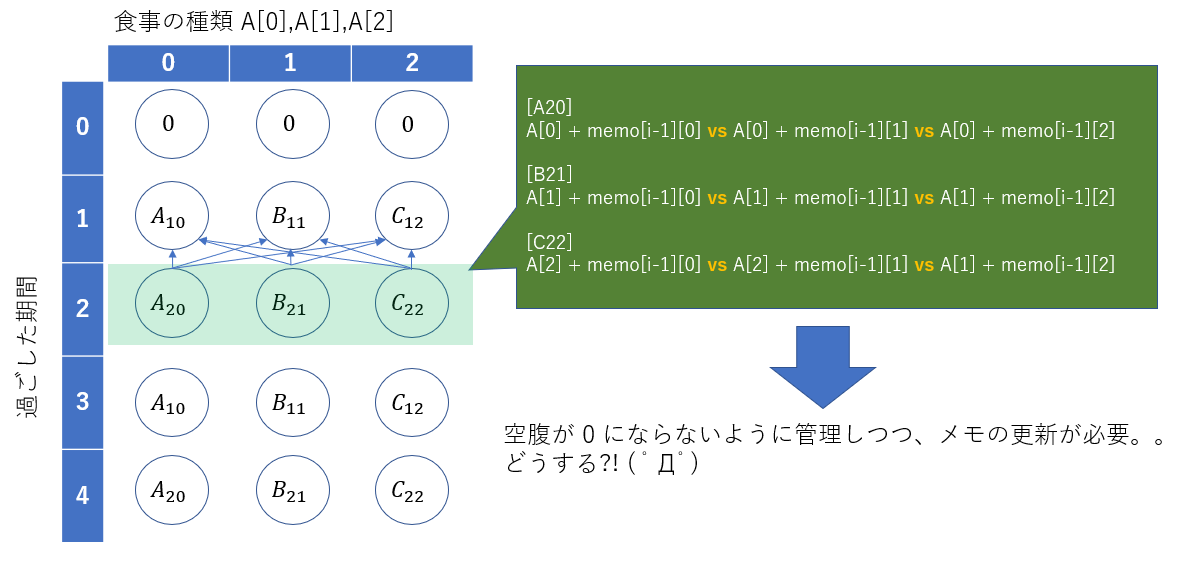
今後、綺麗にするかもしれないですけど、
とり急ぎ別のアイディアをメモレベルですが載せておきます。

横軸を空腹度としました。該当するセルを追いかけてメモを更新するためには
次どこに行くべきなのかを更に別で記録する必要があります。
何やら訳が分からなくなるので、表全部を一個ずつ更新することにします。
# N,H = map(int,input().split())
# A,B,C,D,E = map(int,input().split())
N,H = 4,5
A,B,C,D,E = 100,4,60,1,4
# N,H = 10,1
# A,B,C,D,E = 5000,2,2000,1,300
# INF = float("inf")
# ANS = float("inf")
INF = A*2
ANS = A*2
MAX_LIFE = H+B*N
dp = [[INF for m in range(MAX_LIFE)] for n in range(N+1)]
dp[0][H] = 0
for i in range(N):
for j in range(MAX_LIFE):
if MAX_LIFE - (j + B) > 0:
dp[i+1][j+B] = min(dp[i+1][j+B],dp[i][j]+A)
if MAX_LIFE - (j + D) > 0:
dp[i+1][j+D] = min(dp[i+1][j+D],dp[i][j]+C)
if (j - E) > 0:
dp[i+1][j-E] = min(dp[i+1][j-E],dp[i][j])
for l in range(MAX_LIFE):
ANS = min(ANS,dp[N][l])
print(ANS)
一応、欲しい答えは出たけど、
AtCoder 先生曰く、実行時間制限超過らしい。
厳しいですね(笑)