ナップサックの制限は重さじゃなくて体積だと思うよｗ_11/22update

こんばんは(*´ω｀)
いつも応援有難うございます m(_ _)m

有名なナップサックに挑戦しました。
有識者のコードを斜め見しながら、
何がしたいのかを考察した次第です。

KnapSack.py

class Item:
    def __init__(self,w=0,p=0):
        self.weight=w
        self.price=p

items = [ Item(300,400), Item(500,250), Item(200,980),
          Item(600,340), Item(900,670), Item(1360,780),
          Item(800,570), Item(250,800) ]

def knapsack(i, w):
    if i==len(items):
        return 0
    if w - items[i].weight < 0.0:
        return knapsack(i+1, w)

    Val_sum0 = knapsack(i+1, w)
    Val_sum1 = knapsack(i+1, w - items[i].weight) + items[i].price

    return max(Val_sum0,Val_sum1)

p = knapsack(0, 1200)
print("MAXIMUM TOTAL PRICE is",p)

荷物を入れようが、入れまいが、
トライした回数(試行回数)を i として考えます。
並べられた items は幸いにも制限があり、
与えられた条件内で最大値を求める問題です。

最後まで試行した時に knapsack は 0 を返すことにします。
再帰処理のお約束、ベースケースにこれを定義します。

KnapSack.py

def knapsack(i, w):
    if i==len(items):
        return 0

しかし、これでは話がまとまらないので、
その過程の中で item の値段を加算していきます。

勿論、無限に加算するわけではありません。
定義した重量以内で最大値を求めなければなりません。
よって、item を追加するたびに、定義された最大重量からitemの重量を引いていき、
w - items[i].weigh < 0 になったら、
重量制限を超えるので、items[i] の追加は諦めて
i をインクリメントして次の item の追加を試みます。

KnapSack.py

    if w - items[i].weight < 0.0:
        return knapsack(i+1, w)

めでたく、前述にあるように、
1. 試行(トライ)回数 i　が items 個数以下
2. 重さ制限をオーバーすることがない
条件をクリアして初めて、items を追加するか、しないかを
検討することが出来ます。

KnapSack.py

    Val_sum0 = knapsack(i+1, w)# 追加しない
    Val_sum1 = knapsack(i+1, w - items[i].weight) + items[i].price # 追加する

    return max(Val_sum0,Val_sum1)#どっちがデカい？

前述の記述で、自分がハマったのは、
Val_sum1 = knapsack(i+1, w - items[i].weight) + items[i].price　です。
knapsack に items.price を足す？は？( ﾟДﾟ)
でした。

でも、考えてみると、knapsack は再帰処理なので、最終的には base case に落ちます。
そうです、0 になるのです。そのため、items.price を積み重ねた結果だけが帰ってくるのです。

ではでは、前述の記述は全探索なので、
重複計算が含まれていました。
それを削減していこうと思います。

ただ、出来たけど微妙かもしれません(笑)

knapsack.py

class Item:
    def __init__(self,w=0,p=0):
        self.weight=w
        self.price=p

items = [ Item(300,400), Item(500,250), Item(200,980),
          Item(600,340), Item(900,670), Item(1360,780),
          Item(800,570), Item(250,800) ]

def knapsack(i, w):
    if memo[i][w]:#メモの該当セルに何か入っているか確認。
        return memo[i][w]#入ってたら値を返す、計算削減!!
    if i==len(items):
        return 0
    if w - items[i].weight < 0.0:
        return knapsack(i+1, w)

    Val_sum0 = knapsack(i+1, w)
    Val_sum1 = knapsack(i+1, w - items[i].weight) + items[i].price

    memo[i][w] = max(Val_sum0,Val_sum1) # メモる!!
    return memo[i][w]# メモした値を返す

wgoal = 700

memo = [[[]for k in range(wgoal + 1)] for l in range(len(items)+1)] # 広大なメモ帳を作った(笑)

p = knapsack(0,wgoal)
print("MAXIMUM TOTAL PRICE is",p)

今まで学んできたのはメモを用意して、
過去に計算したものを呼び出すことで計算を削減するチャレンジです。

ただ、今回は用意したメモが広大過ぎる(笑)。
今メモしているのは、
特定の試行回数の時の重さにおける最大価格をメモしています。
重さが、数百である以上は、用意するメモの規模が大きくなってしまいます。
問題の設定ミス!! (*ﾉωﾉ)

因みに、再帰を用いない方法もあります。

knap_dp.py

N = 8 #number of backs
w =[300, 500, 200, 600, 900, 1360, 800, 250]
v =[400, 250, 980, 340, 670, 780, 570, 800]

wgoal = 700
memo = [[0]*(wgoal+1)for l in range(N+1)]

for i in range(N):
    for j in range(wgoal+1):
        if j < w[i]:
            memo[i+1][j] = memo[i][j]
        else:
            memo[i+1][j] = max(memo[i][j],memo[i][j-w[i]]+v[i])

print("MAXIMUM TOTAL PRICE is",memo[N][wgoal])

とても装いがスッキリしました。
再帰処理で重さを色々試していましたが、
for 文に切り替えて i 回目の試行時の
重さを全部書き出しています(DP って言うらしいです)。

読んだり書いたり、何となく動かしている感は否めません。
もうちょっとローカールでイメージづくりをしてしてみます( *´艸｀)。

-11/22_update-------------------------------------------------------------

先日の問題設定ミスを反省して、
チョット変えました、簡単に(笑)

knap_dp.py

N = 3 #number of backs
w =[3, 4, 5]
v =[30, 50, 60]

wgoal = 8
memo = [[0]*(wgoal+1)for l in range(N+1)]

for i in range(N):
    for j in range(wgoal+1):
        if j < w[i]:
            memo[i+1][j] = memo[i][j]
        else:
            memo[i+1][j] = max(memo[i][j],memo[i][j-w[i]]+v[i])
        print(f"i={i},j={j}")    
        for k in memo:
            print(k)
        print()


print("MAXIMUM TOTAL PRICE is",memo[N][wgoal])

取りあえず実行します。

実行結果.py

i=0,j=0
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=1
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=2
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=3
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=4
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=5
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=6
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=7
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=0,j=8
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=0
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=1
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=2
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=3
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=4
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=5
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=6
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=7
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=1,j=8
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=2,j=0
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=2,j=1
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=2,j=2
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 0, 0, 0, 0, 0, 0]

i=2,j=3
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 0, 0, 0, 0, 0]

i=2,j=4
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 50, 0, 0, 0, 0]

i=2,j=5
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 50, 60, 0, 0, 0]

i=2,j=6
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 50, 60, 60, 0, 0]

i=2,j=7
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 50, 60, 60, 80, 0]

i=2,j=8
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 30, 30, 30, 30, 30, 30]
[0, 0, 0, 30, 50, 50, 50, 80, 80]
[0, 0, 0, 30, 50, 60, 60, 80, 90]

MAXIMUM TOTAL PRICE is 90

これだけ見せられて理解できた人は天才です。
私は凡人なので、イメージを作りながら整理していきます。
まずは自分で用意したメモをイメージします。
w は重さです。wgoal に向かって徐々に増えていきます。

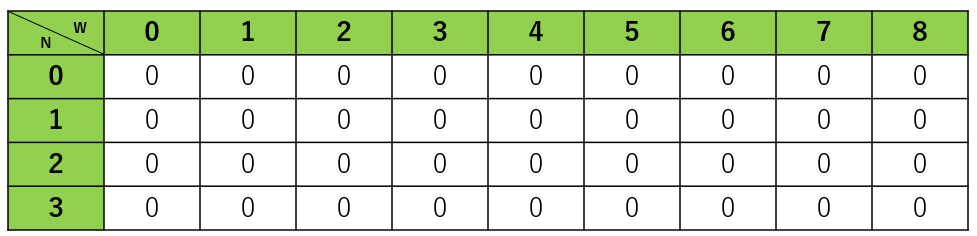
ではプログラムに沿ってみてみましょう。

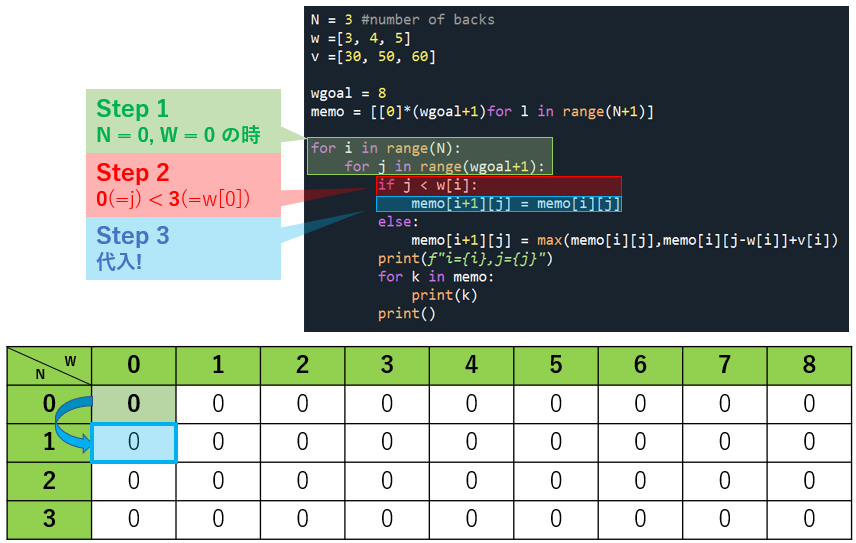
さぁ、ドンドン行きましょう。




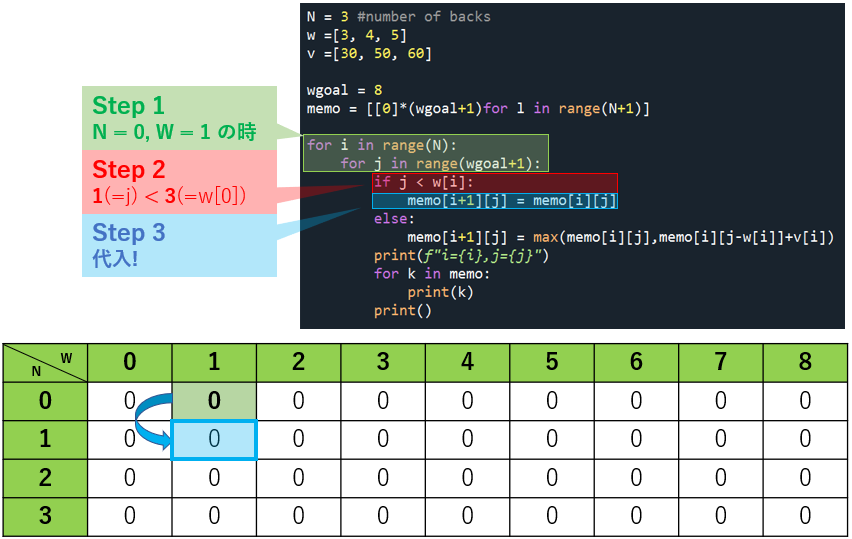
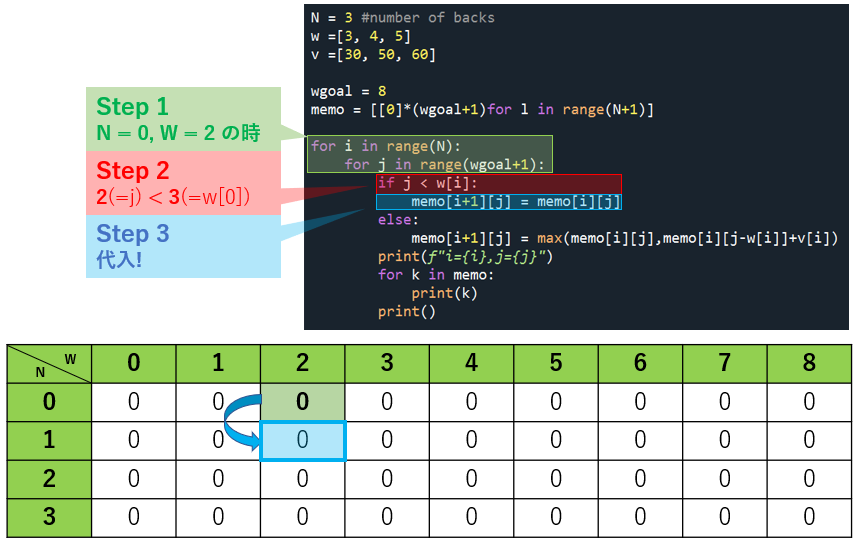
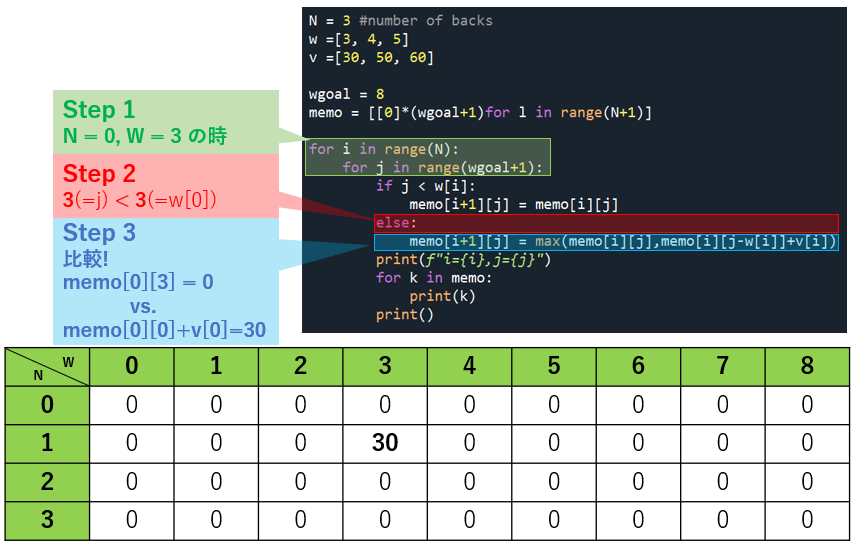
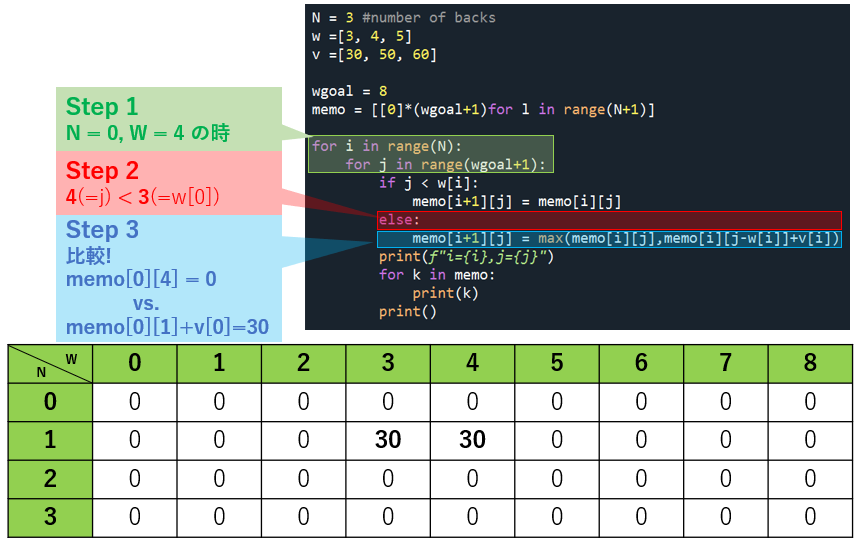
やりたいことが見えてきたので、N = 0 の残りはまとめて行きます。

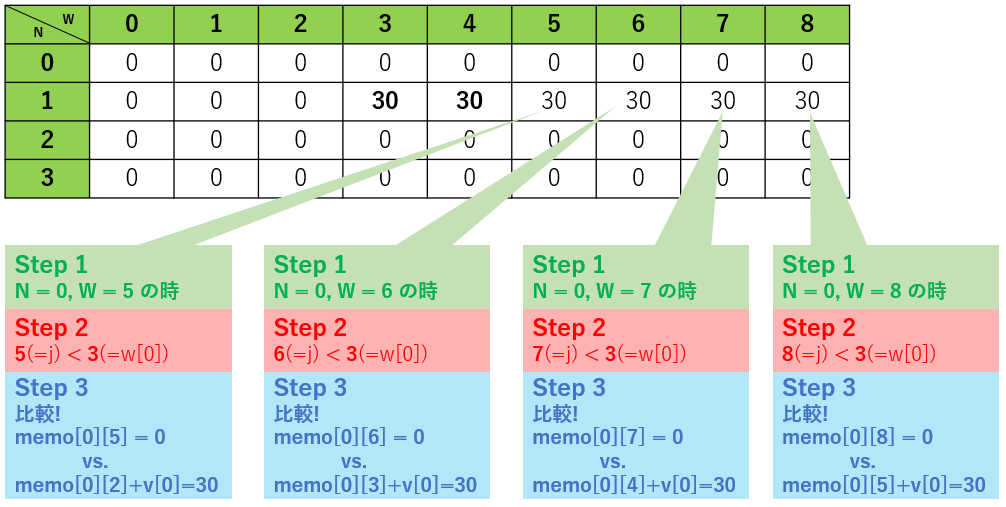
同じ考え方で N = 1 をやってみます。

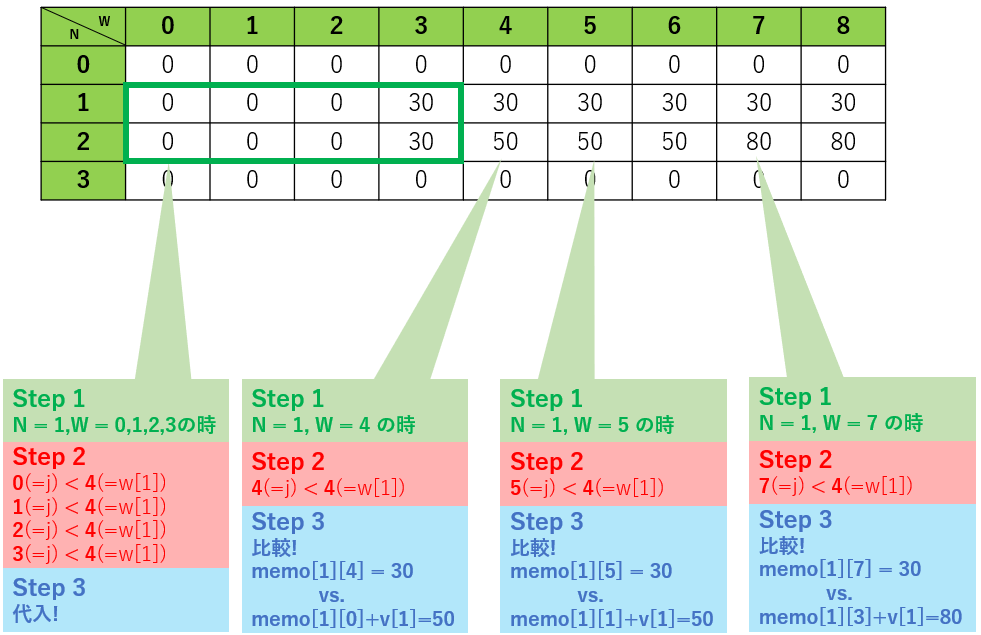
N = 2 もやってみます。

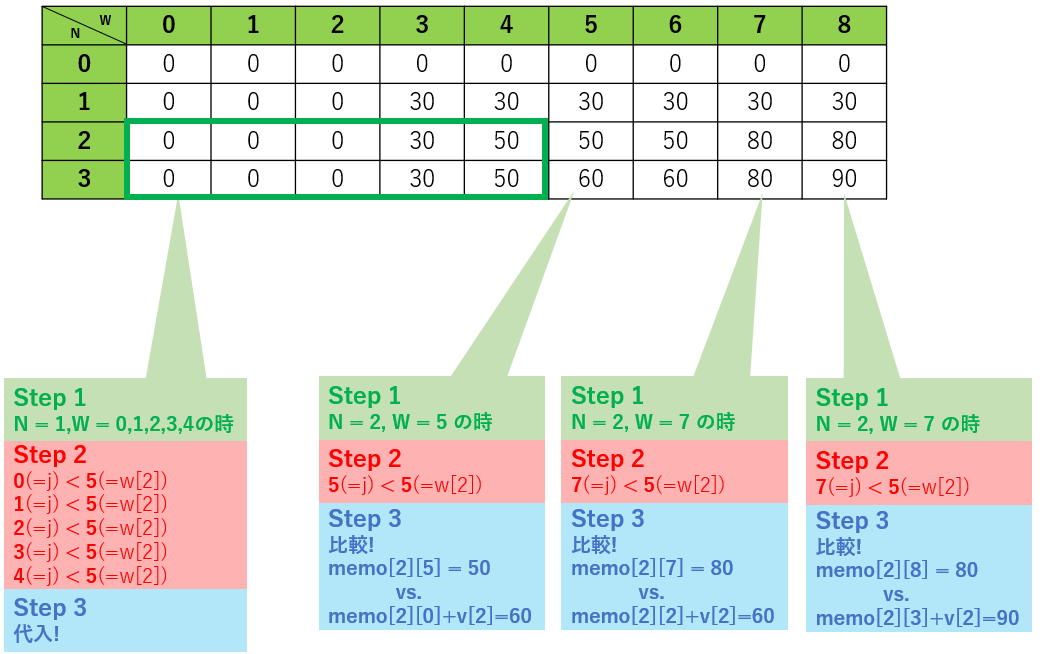
なるほど、90が最大なのですね。
なんとかコードを追うことが出来ましたが、
頭の中で、こんな表作ってるですか？皆さん、天才ですね( ﾟДﾟ)
私は少しずつ練習して地道に行きます( ..)φメモメモ