アイデア
- 光散乱数値シミュレーション終了時の係数をDeep Learning(DL)で学習する
- 学習した係数で別PCで再計算する
- 再計算時、収束が早い
- DLの誤差は再計算により補正されるため、学習の精度を追求しなくてもよい?
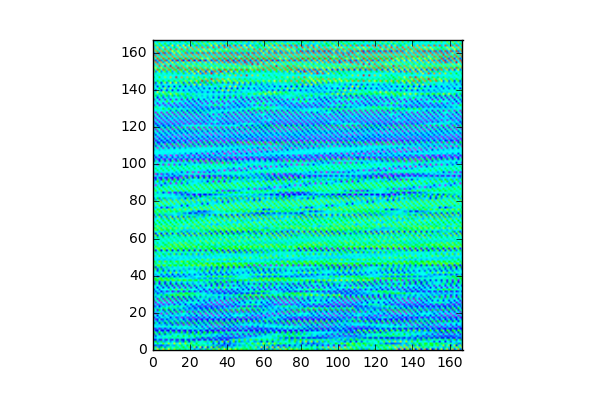
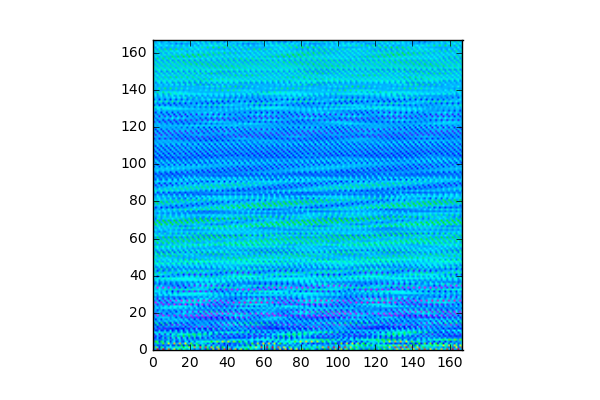
計算がすぐに完了する「球形」で係数の1つ(double complex型xvec[]の実部)を可視化してみた。
コード参考 http://qiita.com/7of9/items/4aa49fce3d524b04312a
計算の実行
http://qiita.com/7of9/items/b79c126b43479a3a124b
## 可視化の目的
- Deep Learningで学習すべき係数の選定
- 全ての係数を学習すべきかどうか確認する
実行
初回
$ ./adda -grid 25 -chp_type normal -chpoint 1s
再開
$ ./adda -grid 25 -chp_type normal -chp_load -chpoint 1s
xvec[]実部 (iteration 156回目)
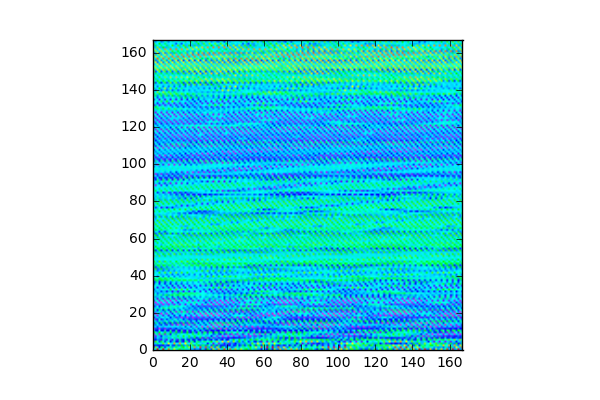
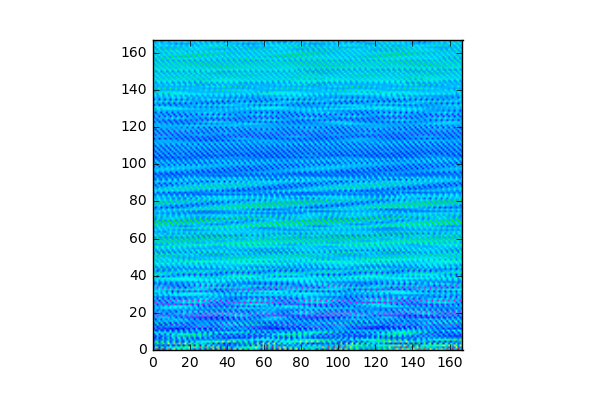
xvec[]実部 (iteration 288回目)
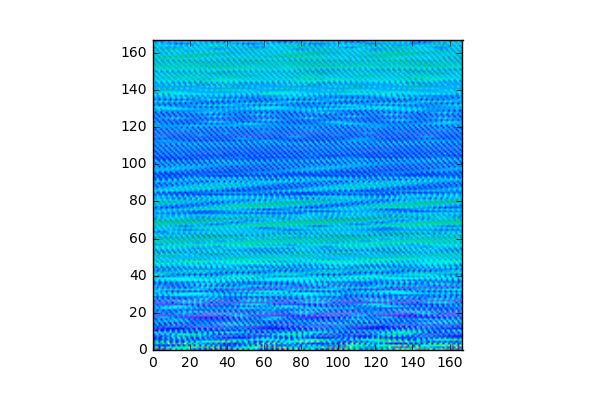
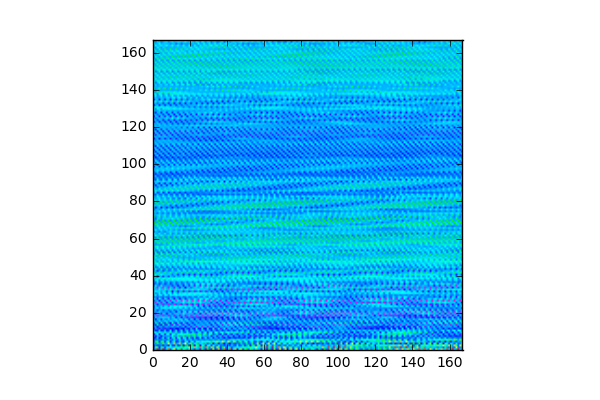
xvec[]実部 (iteration 524回目)
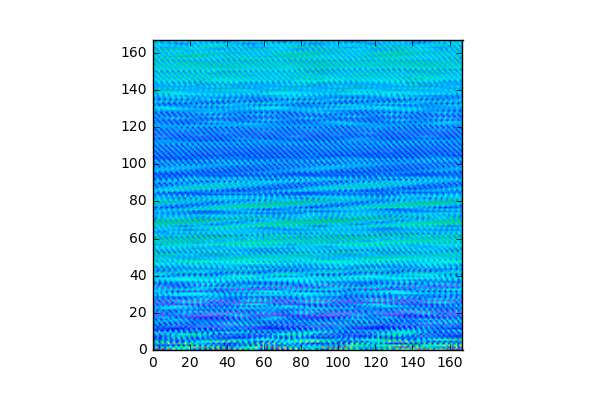
xvec[]実部 (iteration 718回目)
xvec[]実部 (iteration 957回目)
xvec[]実部 (iteration 1144回目)
xvec[]実部 (iteration 1325回目)
xvec[]実部 (iteration 1467回目)
xvec[]実部 (iteration 1695回目)
xvec[]実部 (iteration 1834回目)
xvec[]実部 (iteration 2054回目)
注意事項
- 画像で確認した場合、対数的変化は把握できない
- 対数的変化が線形方程式の解放に影響するかは未調査
メモ
今回の計算では3271回で精度1E-6を達成した。
一度この精度を達成すると、再計算は瞬時に終わる。
検討事項は学習精度20%の誤差で再計算がどれくらい早くなるか。
その確認方法も考えてはいる。