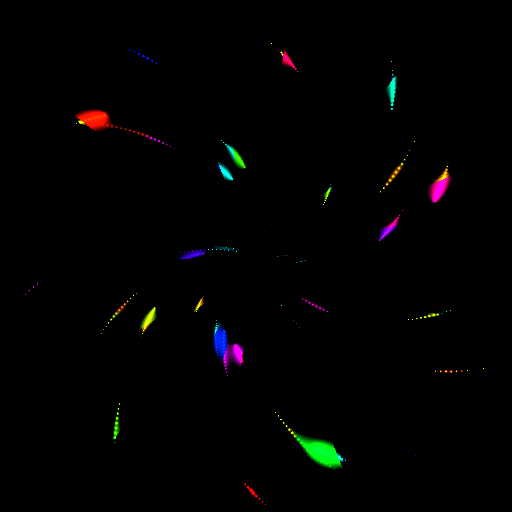[連載 GLSL 物語] チカラが欲しいか……（第三話）極座標リプリケーション

極座標リプリケーション

さっそく、円のディスタンスフィールドの上に円のディスタンスフィールドを描きたいのですが、円のディスタンスフィールドの上に沿って大量の円を描きたいので、リプリケーションをしなければなりません。

極座標リプリケーションをすると言うと何やら難しそうな感じがしますが、

こちらのサイトの一番下の例でディスタンスフィールドで多角形を描くのと一緒です。

• https://thebookofshaders.com/07/?lan=jp

実は多角形を描くのはリプリケーションしていたんですね。

なので、atanで角度を割り出し、分割したい数だけ分割すればいいですね

https://goo.gl/ra2QGP

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 #define PI 3.14159265359
 #define TWO_PI 6.28318530718

 #define N 6.

 void main(void){
  vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
  float r = floor(degrees(atan(p.y,p.x))/N)*N+N/2.;
  //vec2 q = normalize(p)*.8-p;
  vec2 q = vec2(cos(radians(r)),sin(radians(r)))*.8-p;

  float l=step(length(q),.03);
  gl_FragColor = vec4(vec3(l), 1.);
 }

違うのはベクトルディスタンスフィールドを作っているところです。

  //vec2 q = normalize(p)*.8-p;
  vec2 q = vec2(cos(radians(r)),sin(radians(r)))*.8-p;

normalize(p)の代わりにcosとsinを使っていますが、
これは、任意角度の単位ベクトルになります。

これで、無事出来ました！

極座標リプリケーション利用例

極座標リプリケーションを使った集中線 本来、頂点シェーダーでやった方がいい処理です。線の太さが中心から離れても変わらないのが特徴。

https://goo.gl/bdmtAU

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 #define PI 3.14159265359
 #define TWO_PI 6.28318530718

 #define N 60.
 #define N2 15.


 void main(void){
  vec2  p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
  float r = floor(degrees(atan(p.y,p.x))/N)*N+N/2.;
  vec2  q = vec2(cos(radians(r)),sin(radians(r)))*.8-p;
  float r2 = floor(degrees(atan(q.y,q.x))/N2)*N2+N2/2.;
  vec2  s = vec2(cos(radians(r2)),sin(radians(r2)))*.2-q;

  float l=step(length(s),.02);
  gl_FragColor = vec4(vec3(l), 1.);
 }

https://goo.gl/LXAyK9

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 #define PI 3.14159265359
 #define TWO_PI 6.28318530718

 #define N 15.

highp float rand(vec2 co){
 highp float a = 12.9898;
 highp float b = 78.233;
 highp float c = 43758.5453;
 highp float dt= dot(co.xy ,vec2(a,b));
 highp float sn= mod(dt,3.14);
 return fract(sin(sn) * c);
}

 mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

 float crs(vec2 v1, vec2 v2) {
    return v1.x*v2.y - v1.y*v2.x;
}

 void main(void){
  vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
  p=p*rotate2d(t);
  float r = floor(degrees(atan(p.y,p.x))/N)*N+N/2.;
  float l=abs(crs(vec2(cos(radians(r)),sin(radians(r))),p));
  l=step(l,0.005)*clamp((mod(length(p)+t*(1.+rand(vec2(r,r)*2.))+rand(vec2(r,r)),1.5)-.5),0.,1.);
  l+=0.1*(.8+abs(sin(t*7.)*.2))/length(p);
  gl_FragColor = vec4(vec3(l), 1.);
 }

https://goo.gl/A7K6cC

それぞれのリプリケーションの内容をランダムにしてあげるとパーティクルのようにすることもできます。

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 #define PI 3.14159265359
 #define TWO_PI 6.28318530718

 #define N 10.

highp float rand(vec2 co){
 highp float a = 12.9898;
 highp float b = 78.233;
 highp float c = 43758.5453;
 highp float dt= dot(co.xy ,vec2(a,b));
 highp float sn= mod(dt,3.14);
 return fract(sin(sn) * c);
}

mat2 rotate2d(float _angle){
   return mat2(cos(_angle),-sin(_angle),
               sin(_angle),cos(_angle));
}

vec3 hsv(float h, float s, float v){
    vec4 t = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
    vec3 p = abs(fract(vec3(h) + t.xyz) * 6.0 - vec3(t.w));
    return v * mix(vec3(t.x), clamp(p - vec3(t.x), 0.0, 1.0), s);
}

 void main(void){
  vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
  p=p*rotate2d(t);
  float r = floor(degrees(atan(p.y,p.x))/N)*N+N/2.;
  vec2 q = vec2(cos(radians(r)),sin(radians(r)))*(.2+mod(rand(vec2(r,r))+t*(.5+rand(vec2(r,r))),1.))-p;

  float l=0.01/length(q)*.4-length(q);
  gl_FragColor = vec4(vec3(hsv(radians(r)+t/5.,1.,1.)*l), 1.);
 }

モーションブラーをつけるともはや別物ですね。

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 #define PI 3.14159265359
 #define TWO_PI 6.28318530718

 #define N 10.

highp float rand(vec2 co){
 highp float a = 12.9898;
 highp float b = 78.233;
 highp float c = 43758.5453;
 highp float dt= dot(co.xy ,vec2(a,b));
 highp float sn= mod(dt,3.14);
 return fract(sin(sn) * c);
}

mat2 rotate2d(float _angle){
   return mat2(cos(_angle),-sin(_angle),
               sin(_angle),cos(_angle));
}

vec3 hsv(float h, float s, float v){
    vec4 t = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
    vec3 p = abs(fract(vec3(h) + t.xyz) * 6.0 - vec3(t.w));
    return v * mix(vec3(t.x), clamp(p - vec3(t.x), 0.0, 1.0), s);
}

 void main(void){
  vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
  float r,l;
  for(float tt=0.;tt<20.;tt++){
    vec2 s=p*rotate2d(t+tt/80.);
    r = floor(degrees(atan(s.y,s.x))/N)*N+N/2.;
    float d = mod(rand(vec2(r,r))-(t+tt/80.)*(.5+rand(vec2(r,r))),1.);
    vec2 q = vec2(cos(radians(r)),sin(radians(r)))*d-s;

    l+=(0.01/length(q)*.6*d-length(q))*tt/10.;
  }
  gl_FragColor = vec4(vec3(hsv(radians(r)+t/5.,!1.,1.)*l), 1.);
 }

さらにその先に

が、ここまでは実はディスタンスフィールドでも頑張ればできました。

ベクトルディスタンスフィールドが活躍するのは、さらにその先にあります。

ベクトルディスタンスフィールドの上にベクトルディスタンスフィールドを展開できたのならば、さらにその先にベクトルディスタンスフィールドを展開できる筈ですよね。

次回

• [連載 GLSL 物語] チカラが欲しいか……（第四話）さらにその先へ