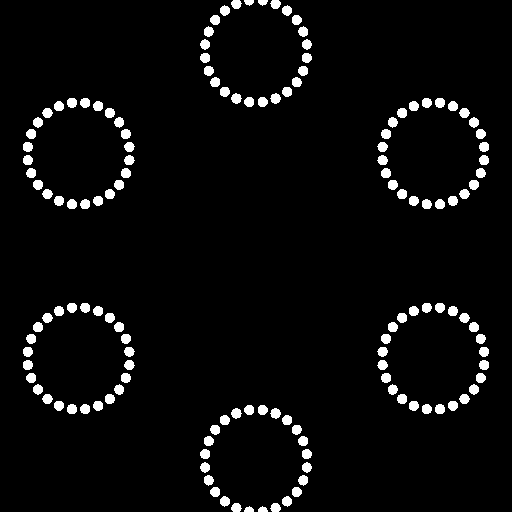
さらにその先へ
ベクトルディスタンスフィールドにベクトルディスタンスフィールドを掛けてさらにベクトルディスタンスフィールドを掛けてみましょう
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
#define PI 3.14159265359
#define TWO_PI 6.28318530718
#define N 60.
#define N2 15.
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
float r = floor(degrees(atan(p.y,p.x))/N)*N+N/2.;
vec2 q = vec2(cos(radians(r)),sin(radians(r)))*.8-p;
float r2 = floor(degrees(atan(q.y,q.x))/N2)*N2+N2/2.;
vec2 s = vec2(cos(radians(r2)),sin(radians(r2)))*.2-q;
float l=step(length(s),.02);
gl_FragColor = vec4(vec3(l), 1.);
}
単純に、ベクトルディスタンスフィールドをチェインするだけでいいですね。
これで、花火のように2段階で分裂するパーティクルのようなものも作ることができますね。
もちろん、さらに、無限にチェインすることができます。かつ、別に円のディスタンスフィールドでなくてもいいんですよ。分割数も、それぞれのチェイン毎に別々でも構わないです。
夢がひろがりませんか?
ベクトルディスタンスフィールドの正体に迫る
ところで、このベクトルディスタンスフィールド(=ディスタンスフィールド)って何者なんでしょう。ディスタンスフィールドは、イラストレーターやSVGのベクターデータと同じで拡大縮小してもジャギが出ないデータです。しかし、イラストレーターやSVGのベクターデータと全く互換性がありません。ディスタンスフィールドをベクトルディスタンスフィールドに戻したとき、同じベクトルデータということで関係性はあるのでしょうか?
もし、このシェーダーの世界にベジエ曲線を持ってこれたら、どれだけ表現力が上がるのでしょうか。フォントも表示できるし、夢が広がりますね。
次回、このベクトルディスタンスフィールドを可視化して正体に迫ります。