[連載 GLSL 物語] チカラが欲しいか……（最終話）ベクトルディスタンスフィールドの正体に迫る

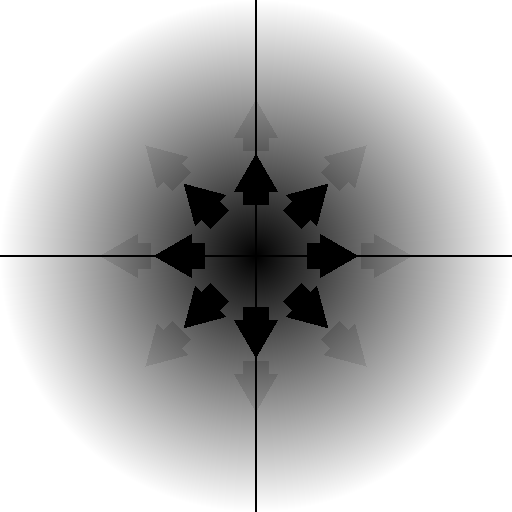
まずは原点を中心としたディスタンスフィールドを可視化してみます。

https://goo.gl/JDmjGv

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 void main(void){
   vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
   float l=0.;
   l=length(p);
   gl_FragColor = vec4(vec3(l), 1.);
 }

正規化されたpをlengthに掛けるだけですね。
原点oを中心に段々距離が遠くなっていきますね。
円状に広がっていきますが、この時点ではまだ形が定まっていません。

https://goo.gl/emfgKe

この時点では普通のベクトル空間です。

次に距離を定めて円を描いてみましょう

https://goo.gl/sGp37W

 precision mediump float;
 uniform vec2  m;       // mouse
 uniform float t;       // time
 uniform vec2  r;       // resolution
 uniform sampler2D smp; // prev scene

 void main(void){
   vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
   float l=0.;
   l=length(normalize(p)*.65-p);
   gl_FragColor = vec4(vec3(l), 1.);
 }

半径を0.65と定めると円が出来ました。
これは、図で見るとなんとなくそうだなと分かります。

https://goo.gl/KQEv9N

でも、このベクトルディスタンスフィールドを可視化すると....。

原点Oが点だったのに対し、原点Oが円状になってる！？
何これキモイ。

ここで、察しがいい人はもう、お分かりかと思いますが、シェーダーアートは原点で描くアートだったんですね。

図形のアフィン変換

ところで、このディスタンスフィールドを移動・回転は正規化されたフラグメントシェーダーが実行されている座標pを操作して移動するのでしたよね。

pを4倍にしたら、図形は1/4に縮小、図形を左に回転させたら右に回転、図形を右に移動させたら左に移動、つまり、pに対する操作なので、逆行列を掛けてるわけですね。図形の拡大・縮小・移動などアフィン変換については通常のベクトル操作の逆行列を掛ければ良いので、ここは問題ありません。

では形の方はどうでしょうか？

極座標リプリケーションを可視化する

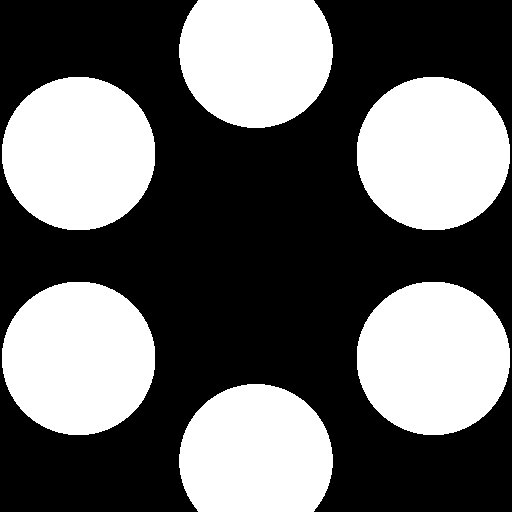
今度は極座標リプリケーションを見てみましょう。

https://goo.gl/CmE2rs

ディスタンスフィールドを表示してみると

https://goo.gl/F28WZt

さらに気持ち悪い図形が浮かび上がってきました。
ベクトルディスタンスフィールドを表示してみると

https://goo.gl/cctW83

原点が6個に増えてますね。

ちなみに、白い境界は、6つに分かれた平行世界の世界線です、この境界は絶対越えられません。iq先生みたいに、物体がはみ出そうになったら、物体の形で境界線を歪ませる。なんてことはできるみたいですけどね。

https://www.shadertoy.com/view/XtSczV

理論上は、この物体の形に境界線を切って動かすことは可能な筈ですが、その場合でも、同一の空間が重なることはできません。但し、平行世界の位相をずらした左右隣の平行世界を重ねることで疑似的に境界線を越えるように見せることは可能です。話が逸れました。これは、また別記事で解説します。

長くなりそうだったので一旦投稿
あとで続き書きます。