はじめに
glslでよく使う、波形関数をまとめています。
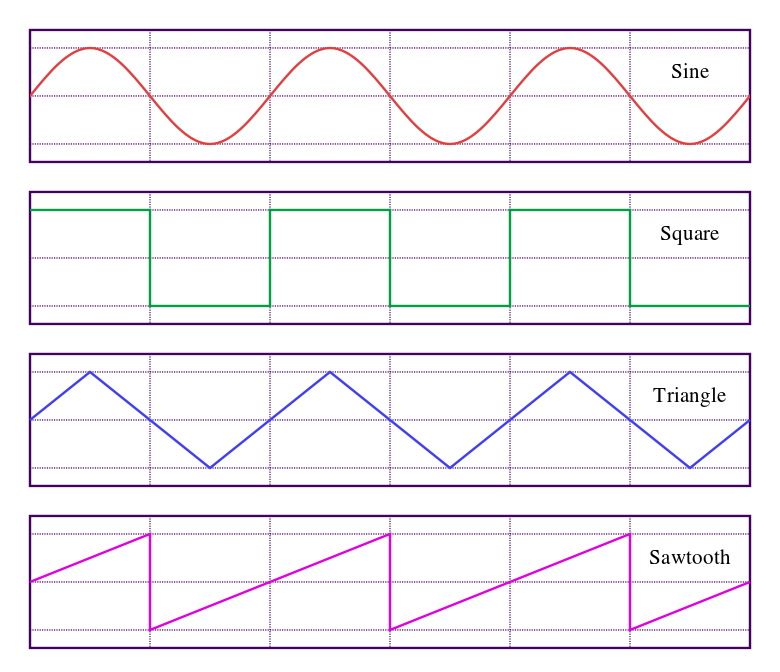
出典 https://ja.wikipedia.org/wiki/%E7%9F%A9%E5%BD%A2%E6%B3%A2#/media/File:Waveforms.svg
正弦波
まずは、基本の正弦波、組み込み関数のsinだけで大丈夫、周期を引数-1.0~1.0の範囲で収めるためにはPIを掛ける必要がある。
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+sin(p.x*PI)));
gl_FragColor = vec4(vec3(l), 1.0);
}
矩形波
基本の矩形波2通りの作り方がある
sin波のパターンは極座標系で、それ以外はfractのものを使った方がいいでしょう。
sinとstepを組み合わせたパターン
こちらは分かりやすい
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
float sqr(float x){
return 2.*(step(0.,sin(x*PI))-.5);
}
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+sqr(p.x)));
gl_FragColor = vec4(vec3(l), 1.0);
}
fractとstepを組み合わせたパターン
恐らくこちらの方が軽い
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
float sqr(float x){
//return 2.*(step(0.,sin(x*PI))-.5);
return -2.*(step(.5,fract(x*.5))-.5);
}
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+sqr(p.x)));
gl_FragColor = vec4(vec3(l), 1.0);
}
のこぎり波
ようするにfract関数やmod関数ですね。 使いやすいように位相をずらしてます。
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
float saw(float x){
return fract(-x*.5)*2.-1.;
}
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+saw(p.x)));
gl_FragColor = vec4(vec3(l), 1.0);
}
三角波
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
float tri(float x){
return abs(2.*fract(x*.5-.25)-1.)*2.-1.;
}
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+tri(p.x)));
gl_FragColor = vec4(vec3(l), 1.0);
}
- sinとasinを使った三角波、周期がPIのときはこっちが良さそう
precision mediump float;
uniform vec2 m; // mouse
uniform float t; // time
uniform vec2 r; // resolution
uniform sampler2D smp; // prev scene
const float PI = 3.14;
const float PI2 = PI* 2.;
float tri(float x){
return asin(sin(x*PI))*2./PI;
//return abs(2.*fract(x*.5-.25)-1.)*2.-1.;
}
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l=length(vec2(0,p.y+tri(p.x)));
gl_FragColor = vec4(vec3(l), 1.0);
}
最後に
より複雑な波形を作るときにはiq先生がエディターを作っているので、こちらの Graph Toy を活用すると良いでしょう。



