#概要
次元の呪いとは次元数が増えることで計算時間が指数関数的に増大する、というのが一般的だが
今回は機械学習における次元の呪いについて学んだことをメモしました
機械学習における次元の呪いとは
データが高次元になると予測精度が悪くなる現象
主な原因
・学習データの不足
・高次元空間の特殊な性質
#学習データ数の不足
まず10000レコードあるデータを考え、それらは10通りの値の変数をもつとする
この変数の数が2つだと、表現できるデータの組み合わせは10の2乗で100通り
しかしこの変数が10あると10の10乗で100億通りとなる
これにより学習データとデータの組み合わせの比が
変数の数によって小さくなります
よってデータ空間内にデータがほとんどなく(データ空間が疎)
データ空間にデータのないところが多いにもかかわらず
その場所に対しても予測を立てなければならないため予測精度が悪くなります
##過学習とは
過学習とは学習データに対応しすぎて汎用性が失われることです
詳しい解説
#高次元空間の特殊な性質
まずは5通りの値(1~5)の変数が2つ(変数x,変数y)ある空間を考える
これは5×5の二次元空間である
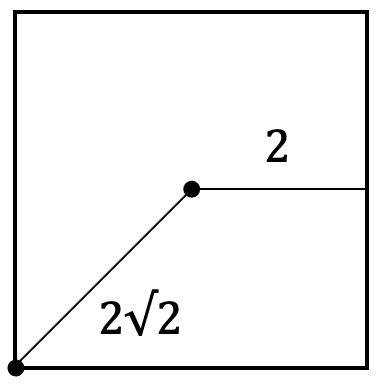
今回は1辺が長さ5の正方形を考えてみる
正方形の中心から面（正方形では辺）までの距離は2
正方形の中心から各頂点までの距離は、2×√(次元数)である
詳しい解説
また３次元を考えると、1辺5の立方体になる
中心は(3,3,3)で各面までの距離は同様に2
各頂点(1,1,1),(1,1,5),(1,5,1)...までの距離は√(2^2+2^2+2^2)=2√3である
これを一般的に考えると
中心から各頂点までの距離を計算するときに
次元数に応じて、各座標の差分の計算が増えることから
(各頂点までの距離)＝√{(各面までの距離の２乗)×(次元数)}
＝(各面までの距離)×√(次元数)
であることがわかる
つまり、次元数が増えるにつれて中心から頂点までの距離は大きくなるが
面までの距離は変わらないということです
これが高次元空間の特殊な性質です
この性質によって、距離による類似度の計算だと
中心付近のデータが学習に高い頻度で採用され
機械学習がうまく働かないということが起こってしまいます
また高次元空間の特殊な性質として
球面集中現象というものもあります
詳しい解説
次に半径・表面付近の定義はそのままで、三次元の球を考えると
(球の体積)=π×1×1×1=πで変わらないのに対して
(表面付近の体積)=(球の体積)-(半径0.9の球の体積)
=π-π×0.9×0.9×0.9≒0.27π
よって表面付近の体積は全体の27％ということが分かります
2つの例から次元が増えると、半径(0.9)をかける回数が増え
内側の体積が減少するのが分かります
逆に表面付近の全体に占める割合は大きくなっています
つまり高次元空間では球の体積のほとんどが
球の表面近くになってしまうということになります
これの球をメロンパン、表面付近をメロンパンのサクサク部分（皮）に例えて
サクサクメロンパン問題という人もいます笑
この球面集中現象の何が問題なのかというと
ほとんどのデータが表面付近になるということは
中心に近い部分がなくなることを意味し
それによって類似していると考えられていた学習データが
変数が増えるごとに少なくなり重要度の高い変数がわからなくなる
という問題が発生してしまうのです
#さいごに
今回は次元の呪いについて調べる機会があったので
自分なりにまとめてみました
図や計算を使うと、高次元空間が自分のイメージと大きく異なることが分かり
説明変数が増えることでこんなことが起こるのかと深く実感できました
これからもわからないことを調べたときに自分なりにアウトプットする媒体として
Qiitaを活用していきたいと思います