学習サイト
統計web
箱ひげ図
データがどのあたりの値に執しているかを一目で捉えるためのグラフ
↓ 男性15人の体重を測定した結果
| No | 体重 [kg] |
|---|---|
| 1 | 52 |
| 2 | 55 |
| 3 | 65 |
| 4 | 80 |
| 5 | 73 |
| 6 | 63 |
| 7 | 68 |
| 8 | 59 |
| 9 | 60 |
| 10 | 57 |
| 11 | 61 |
| 12 | 77 |
| 13 | 79 |
| 14 | 54 |
| 15 | 110 |
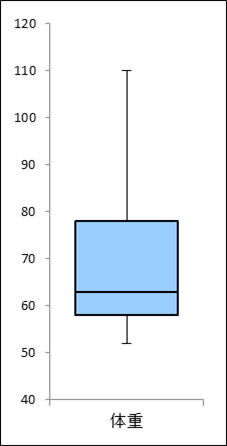
上記の結果を箱ひげ図にすると以下のような箱ひげ図が作られる。
この箱ひげ図を確認すると、以下のことが容易に確認できる
- 最小値 = 52
- 最大値 = 110
パーセンタイル
- データを小さい順で並べた時、ある数値がデータの小さい方から見て何%の位置にあるかを表すもの
- 最小値は0、最大値は100を表す
- Nパーセンタイルは、データ全体をN%と100-N%で分ける値
四分位数
- 25%(全体の1/4の部分) = 25パーセンタイル = 第一四分位数
- 50%(全体の2/4の部分 = 全体の1/2の部分) = 50パーセンタイル = 第二四分位数
- 75%(全体の1/4の部分) = 75パーセンチタイル = 第三四分位数
-
5数要約
- 最小値、第一四分位数、中央値、第三四分位数、最大値の5つの値の総称
- 範囲
- 最大値から最小値を引いたもの
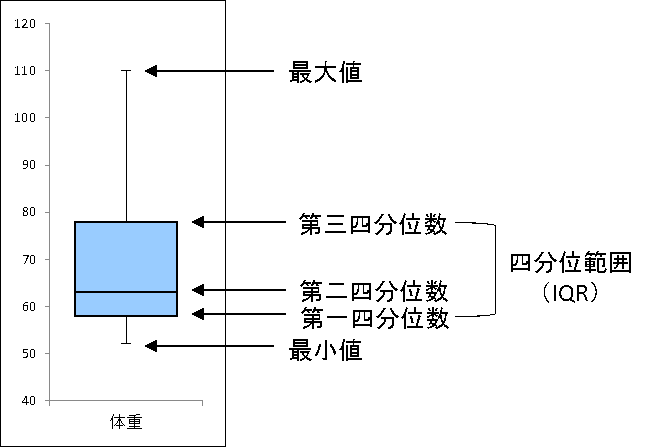
四分位数の値を箱ひげ図に当てはめると以下の通りになる
箱ひげ図とデータの数
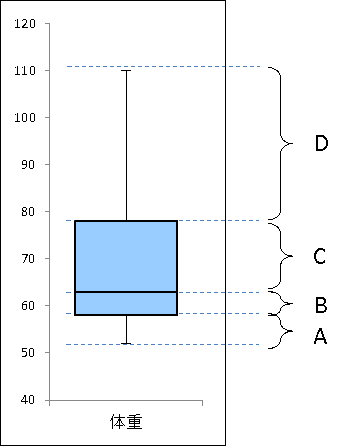
四分位数によってデータは次の4つに区分できる
- 区間D
- ひげの上端(最大値)から箱の上端(第三四分位数)まで
- 区間C
- 箱の上端(第三四分位数)から箱の中央の線(中央値)まで
- 区間B
- 箱の中央の線(中央値)から箱の下端(第一四分位数)まで
- 区間A
- 箱の下端(第一四分位数)からひげの下端(最小値)まで
区間A, B, C, Dの4つの区間の中にはそれぞれ同じ数だけのデータが入っている
しかし、同じ個数であっても、その区間の長さが異なることから、データのばらつき具合を知ることができる
例えば、区間Bと区間Dでは、区間Bの方が区間が短いことからデータが集中していることがわかる
また箱の高さは、全データの半分のデータを表すことから、およそ57から78の範囲に全体の半分のデータが存在することがわかる
外れ値の扱い
外れ値とは、データの分布において、他の観測地から大きく外れた値のこと
外れ値は、測定ミスや異常があって観測された場合などが考えられるため、データの解釈を困難にさせることがあるため注意が必要
幹葉表示(みきはひょうじ)
- データの値そのもを用いて作成するヒストグラムに似た図のこと
- 幹葉図ともいう
例えば「27, 30, 33, 33, 37, 41, 45」というデータがあった場合、幹葉表示は次のようになる
| 幹 | 葉 |
|---|---|
| 2 | 7 |
| 3 | 0 3 3 7 |
| 4 | 1 5 |