はじめに
この記事は完全に理解したTalk Advent Calendar 2020の14日目の記事です。
前回は遺伝的アルゴリズムの入門編のような記事を書いてみたのですが、自分で読み返しても「具体的な処理が分かりにくい！」と思ったので、今回は具体的なアルゴリズムの流れを示してみたいと思います。
動作環境
- 紙
- ペン
- サイコロ(6面体)
問題
y=x^2を最小にするxを-1 <= X <= 1の範囲から求める
概要
人間は微分とか式変形というエレガントな方法で厳密解を求めることができる問題ですが、アルゴリズムにとってはそうではありませんね。「いやニュートン法で解けるでしょ」というツッコミはなしで。
解くこと自体には全く意味のない問題ですが、ベーシックなGAの動きを理解するにはうってつけの問題かと思い、設定してみました。特定の言語によらない手法なので、今回は手を動かしてトライしてみたいと思います。
遺伝子型
今回の問題を解くにあたり、以下のような6bitのベクトルを遺伝子として設定しました。
- [-1, 1]の範囲を2^6(=64)等分する
- 各ポイントに2進数で番号をふる
- その2進数表記の各桁を成分とするベクトルを遺伝子とする(x=-1は[0,0,0,0,0,0]でx=1は[1,1,1,1,1,1])
- つまり最適解は31(=[0,1,1,1,1,1])もしくは32番目(=[1,0,0,0,0,0])となるときである
評価関数
- 評価関数はシンプルにy=x^2であり、yの計算結果が小さければ小さいほど適合度(Fitness)が良い
- でも直接的には代入できないので、「①遺伝子ベクトルを2進数表示」「②2進数を十進数化」「③十進数化した番号から対応するxを求める」「④xを代入してyを求める」という順番で適合度の計算を行うことになる
計算終了条件
最適解である[0,1,1,1,1,1]もしくは[1,0,0,0,0,0]が求められるまで。
できれば、最適解到達後も、なるべく時間と手首が許す限りサイコロを振って世代交代による適合度の平均値の挙動を確認する。
パラメータ
- 個体数=6
- サイコロが6面体なのでちょうどいいから。
- 初期個体のベクトル成分はサイコロを振って3以下なら0、4以上なら1とする。
- 交叉率=0.5
- 各個体に対してサイコロを振り、3以下なら交叉しない、4以上なら交叉する。
- 交叉する個体に対してもう一度サイコロを振り、出た目で交叉相手と交叉位置を決める。
- 突然変異率=1/6=0.1666…
- 各個体に対してサイコロを振り、1以外なら突然変異しない、1なら突然変異する。
- 突然変異する個体に対してもう一度サイコロを振り、出た目の位置の成分を反転する
- エリート保存戦略=上位1個体
- 各世代で最も適合度の良い個体をエリートとし、交叉も突然変異も行わず次世代に引き継ぐ。
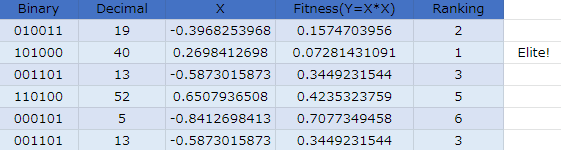
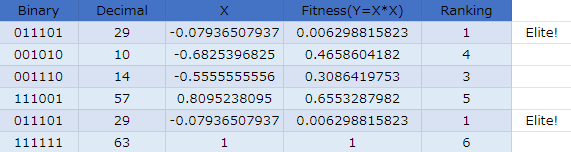
第1世代(初期世代)
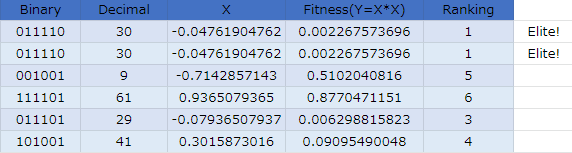
まずランダムに個体を生成しました。
各個体の適合度は以下のとおりです。問題が単純なこともあり、初期個体の中にすでに優秀なのが1個居ますね。
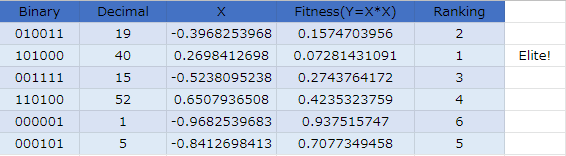
エリートである個体2を除き、交叉処理の要否をサイコロで決定します。
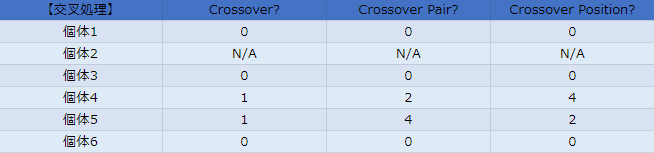
交叉結果です。個体4は成分4より後ろを個体2の成分で上書き、個体5は成分2より後ろを個体4の成分で上書きしました。
次に突然変異処理の要否をサイコロで決定します。こちらもエリートである個体2は除きます。
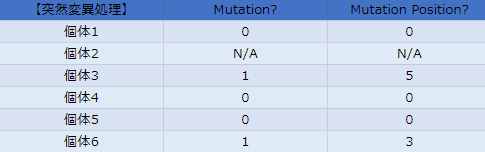
突然変異結果です。
以上の処理を持って第1世代の演算を終了し、出来上がった個体群を第2世代に引き継ぎます。
毎世代全部載せると記事がめちゃくちゃ長くなるので、各世代の最初の適合度計算の結果だけここには載せていきますが、私は腱鞘炎に怯えながらサイコロを振りました。
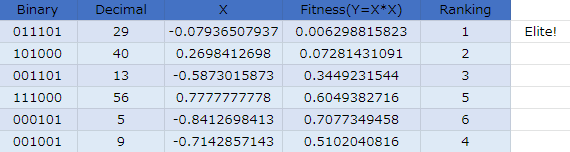
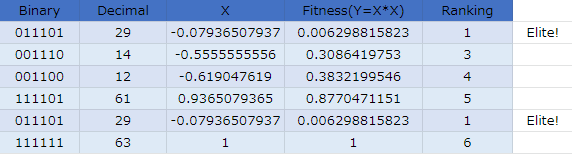
第2世代
個体2が引き続きエリート。適合度が他の個体と比べて1桁違うので仕方ないですね。
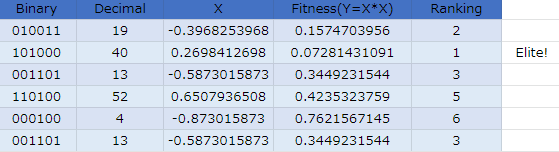
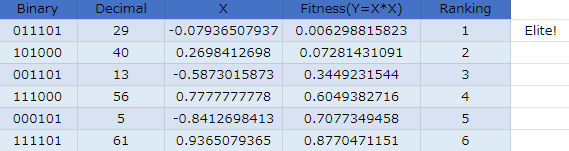
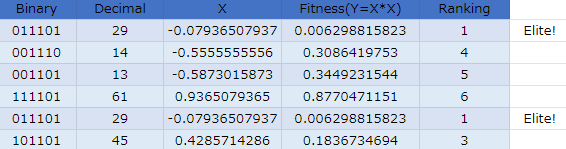
第3世代
個体2の牙城崩れず。
第4世代
個体1が下剋上してエリートに。最適解にかなり近づきました。
第5世代
第6世代
第7世代
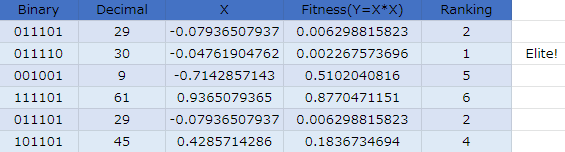
なんとエリート個体が2つ出来てしまいました。あんまり想定していなかったのですが、同率1位なので2個体とも残すことにします。
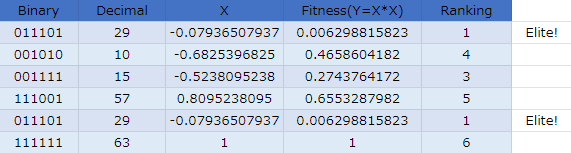
第8世代
第9世代
第10世代
なかなか学習が進みません。正直10世代くらいで終わると思っていたので焦ってます。
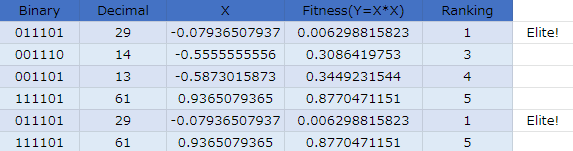
第11世代
第12世代
あと1歩で最適解というところまで来ました。
第13世代
再びエリート個体が複数登場しました。
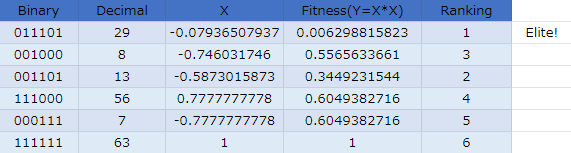
第14世代
はい、第14世代目で遂に最適解である[0,1,1,1,1,1]に到達しました。
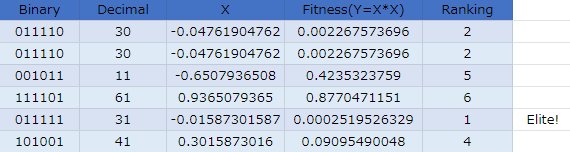
第15世代～第25世代
最適解に到達してしまったのでエリート個体の適合度がこれ以上良くなることはありませんが、25世代目まで頑張りましたのでグラフでダイジェストを提示します。
エリート個体を1個体保存しているので、Bestのグラフは単調減少になっています。エリート個体を保存しない場合は上がったり下がったりしながらだんだん減少してくようなグラフになるはずです。
それに対してAveのグラフは交叉や突然変異といった乱数を使った処理を行うことで、最適解到達後も解が収束することなく探索を継続している模様がわかります。