はじめに
この記事は完全に理解したTalk Advent Calendar 2020の6日目の記事です。
ぶっちゃけQiita様に挙げられるような実用的な話ってあまり持っていない身なのですが、星影さんから下記のようなメッセージを頂いたのでトライしてみることにしました。
一般受けとか気にせずOKなので、ぜひお願いします🤗
— 星影 (@unsoluble_sugar) November 17, 2020
Qiitaは完全に今までROM専だったため、この記事が初投稿になります。Markdownでサクサクかけてめっちゃ便利ですね。不謹慎な記事を上げていいならTumblrから移りたいレベル。
遺伝的アルゴリズム
さて、本日私が完全に理解したのは、遺伝的アルゴリズムです(Uber Eats風)。
Wikipedia先生による簡潔な説明は以下の通りです。
遺伝的アルゴリズム(いでんてきアルゴリズム、英語:genetic algorithm、略称:GA)とは、1975年にミシガン大学のジョン・H・ホランド(John Henry Holland)によって提案された近似解を探索するメタヒューリスティックアルゴリズムである。
すごいざっくり説明すると、厳密な最適解ではないけど、そこそこ実用的な解を限られた時間で捻り出すのに使えるアルゴリズム、のような感じです。いわゆるメタヒューリスティクスの一種です。
余談ですがメタヒューリスティクスって、GA以外にもアリの巣とか魚群とか焼きなましとか、自然の摂理的なものから発想されたものがあって面白いですよね。
GAは作り込み次第でかなり汎用的な使い方ができるので、実はいろんなものに応用されています。
- 巡回セールスマン問題
- N700系のぞみ先頭車両の形状の設計
- 菊川怜の東大卒業研究(コンクリートの最適強度探索)
- アストロノーカの害獣の進化アルゴリズム
- ルービックキューブを揃える
- スーパーマリオブラザーズを学習させてみた
- ロックマンエグゼに人工知能を搭載してみた
実用例を見ると非常にカオスです。それだけ汎用性があるということでしょうか。
概要
前項のニコ動とかYouTubeの動画にわかりやすく紹介されていますので要点だけ紹介します。
- 初期世代の個体生成
- 評価関数で各個体の適合度を評価
- ルーレット戦略などでランダムに自然淘汰を実行
- 現世代の個体内でランダムに交叉処理を実行
- 交叉後の個体に対しランダムに突然変異を実行
- 2に戻る
とまぁ、ざっくり書くとこんな感じで世代交代を繰り返し、終了条件を満たすまで延々とループさせます。
アルゴリズム設計のポイント
GAは汎用的な最適化アルゴリズムであり、難しい処理も特にないので、現実問題に適応する際にはアルゴリズムの設計が性能を大きく左右します。
【遺伝子型】
GAでは遺伝子と読んでいますが、数学的にはベクトルとか行列とかテンソルに相当するものです。プログラム上では配列だと思ってもらえればOKです。
プログラム上では配列ではなくポインタを駆使して動的に遺伝子を表現することもできるのですが、私はあまりおすすめしません。記述が煩雑になりメンテ性がすごい下がるので。
スーマリの動画では1フレあたりの入力キーを並べてベクトルにし、それを遺伝子といていましたね。この場合は1つの遺伝子が必ず1プレイとして表現できますが、遺伝子の設計によっては「遺伝子としては書けるけど、遺伝子内で情報の矛盾や競合があるため現実的に表現できない」という場合があります。これを致死個体と呼びます。GAでは、この致死個体がなるべく起こりにくい遺伝子型に設計することがキーポイントとなります。
あと実用的には遺伝子ベクトル成分を0と1のブール型で表現するか、それとも実数型で表現するか、という悩みもあります。
【評価関数・適合度】
遺伝子型と並んでかなり重要な設計項目です。自分のほしい解をダイレクトに表現できる評価関数が望ましいです。
評価関数は1つで設計することもできますし、複数設計することも可能です。例えば「評価関数1が最小値0となるのは大前提として、その次は評価関数2の最大化を図る」みたいな感じです。この例は辞書式ですが、両者がトレードオフする場合はパレート最適を選ぶやり方もあります。
【個体数】
1世代あたりに生成する遺伝子ベクトルの数です。多ければ多いほど解の探索効率が上がりますが、メモリ量を食うので現実的な数値に設定する必要があります。
個体数をシミュレーション中に可変にすることもできますが、基本的には静的に配列を使って書いてしまうほうが良いと思います。ポインタの記述が面倒くさすぎて自分は断念しましたし、あまり可変にするメリットがないので。
【自然淘汰率】
各世代の適合度を評価してランキングを作成し、何位以下を淘汰するのか、というパラメータです。自然淘汰はしない場合もありますが、局所解に陥りやすいので、ほぼほぼ行うことになると思います。
かといってあまり高く設定すると前世代の情報が引き継がれにくくなって逆に学習が非効率になる場合もあります。
また、「エリート保存戦略」という処理を行うこともあり、上位個体を一定数なんのランダムな操作も加えないまま次世代に引き継ぐことで学習の安定化を図ります。
【交叉率】
現世代に対してどれくらいランダムに交叉(ベクトルの部分的な交換)を行うかというパラメータです。そもそも交叉の方法にも色々あって、1点交叉・2点交叉・多点交叉とかあります。
交叉率というのも、そもそも交叉処理のなんの部分の確率を意図しているかは交叉の手法によってマチマチですが、低すぎても高すぎても学習が非効率になるので、ある程度妥当な値を探る必要があります。
【突然変異率】
交叉後の新世代に対してランダムで突然変異を起こすパラメータです。要するにベクトルの一部を強制的にランダム値と置き換えます。淘汰と交叉だけでは局所解からなかなか抜けられないタイプの問題に対して有効な場合があります。
これも低すぎても高すぎても学習が非効率になるので、ある程度妥当な値を探る必要があります。
【世代交代数】
GAの終了条件にはいくつか考え方があり、「所定の世代数経過する」「所定の目標値まで適合度が到達する」「解が最適化される勾配が一定%を下回ったとき」「現実時間で一定時間経過する」などがあります。が、一般的には世代交代で終了させることが多いと思われます。そもそも適合度については最適解に至ったとしても目標値まで到達できない場合(理想が高すぎる)に計算が終わらないことがあるのであまりおすすめできません。
世代交代を長く設定すれば得られる解がより良くなる場合もありますが、計算時間が長くなる、あるいは所定時間で計算を終わらせるためにハイスペックマシンが必要になる、というデメリットがあります。問題によってはある程度の世代交代数で解がサチる場合もあるので、妥当な交代数を探す必要があります。
ハイパーパラメータの設定めんどくさくね?
はい、面倒くさいです。必ずこうしておけば良い、というものでもないので、実用的には予備実験を繰り返してある程度まで当たりをつけておくことになるかと思います。
ハイパーパラメータまで含めて最適化させる「メタGA」みたいな概念もありましたが、結局実用化されずに廃れた歴史があります。結局計算量が多くなって非効率だったということでしょう(適当)。
コードは?
「Shut the fuck up and write some code」の精神でコードを書いてもよいのですが、GAってあくまでアルゴリズムなので、解くべき問題がないとコードが書けないことをお許しください。Qiitaを見ると色んな人がコードを挙げてますので参考になると思います、多分(適当)。
極論するとGAのコードは問題に対して一品一様で作り込むので、ドンピシャの参考ってないんですよね。
おわりに
いわゆるトイプロブレムなので参考になるかどうかはわかりませんが、太古の昔、自分が初めてGAを触ったときに勉強でOneMax問題(2値ベクトルの成分が全部1だと満点になる問題)を解いたときの実行例を示します。GAの実行イメージの一助になれば幸いです。
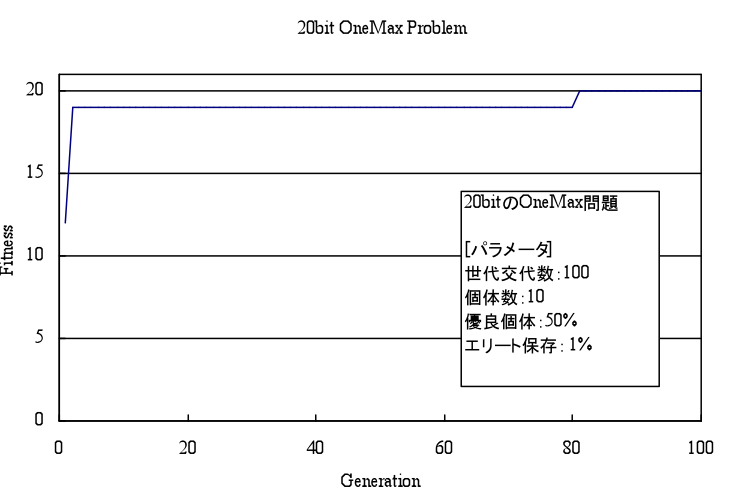
私がGAをよく使っていた頃はまだGPGPUとか一般じゃなくて、「一部のオタクがCudaとか言ってるな」みたいな時代だったのですが、今はGPGPUが一般的になってきたのでかなり計算負荷が軽いのではないかと思います。当時かなり非力なCPUでシミュレーションしていましたが、それでもぼちぼち現実的な時間で実用解が出ていましたので。ちなみに当時私はC++遣いでした。今となってはもはや書けない。
参考文献
- 安居院猛,長尾智晴:ジェネティックアルゴリズム(1996) ,昭晃堂
- 伊庭斉志:進化論的計算手法(2005),オーム社
- 佐久間淳,小林重信:確率分布推定に基づく実数値 GA の新展開(2003),人工知能学会誌 18巻 5 号 p.p.479-486
- 鈴木譲:遺伝的アルゴリズムへの統計力学的アプローチ(2005),Computational Intelligence Seminar(8 November,2005,Waseda University,Tokyo,Japan) p.p.1-17
- J.Bean:Genetic Algorithms and Random Keys for Sequencing and Optimization(1996),ORSA.J.COMP Vol.6 No.2 p.p.154-160
- 三宮信夫,喜多一,玉置久,岩本貴司:遺伝的アルゴリズムと最適化(1998),システム制御情報学会