0.目的
クラスの多重継承を許す場合、継承の循環の起こり方が複雑になる。
そのような場合に循環継承を効率的に見つけるアルゴリズムを考えてみる。
1.循環継承とは
そもそも循環継承とは何か。
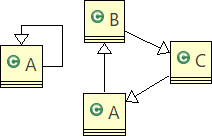
視覚的には図1.1のように、「継承の単方向輪」ができることである。
図1.1 単一継承の場合の循環継承の例
これを言葉で説明すると、「自分が自分自身の先祖や子孫となる」関係である。図1.1の例では、AはA自身の曾祖父母あるいは曽孫であるといえる。
多重継承の場合、直系が複数通りになるため、「どの直系で循環継承が起きているか」を考える必要が出てきてしまう。
2.考案するアルゴリズム
すべての「子クラスを持たないクラス$c0$」に対して次の方法を適用することで、系内の循環継承を見つけることができる。但し、$ci$は$c0$の直系尊属$i$親等な任意のクラスである。
- $i=0$とする。
- $ci$の子孫集合$D_1$を考える
- $ci$の親の配列$Ci+1$を考える。
- $Ci+1$の各元$ci+1$の子孫集合$D_2$を考える。
- $ci+1$の循環参照がないことの真偽は$D_1 \cap D_2 = \phi$と同値である
- $i$をインクリメントする。
なお、このアルゴリズムには次の2つの定理を採用している。
- すべての「子を持たないクラス」の先祖を辿れば、系内全てのクラスにアクセス可能である (2-1節で詳解)
- 子孫に$d$を持つクラス$c$の任意の親$p$が子孫に$d$を持つことと、$p$が循環継承していることは同値である (2-2節で詳解)
2-1.系内全てのクラスに最低1度は確実にアクセスする方法
すべての「子を持たないクラス」の先祖を辿れば、系内全てのクラスにアクセス可能である
全てのクラスは「子を持たないクラス」と「子を持つクラス」に分けられる。
「子を持つクラス」は何かしらのクラスから見た親クラスである。
いま、クラスについて①②に場合分けして考えよう。
「子を持つクラス」の子が「子を持たないクラス」である場合、子の先祖を辿ることでアクセス可能だ。・・・①
「子を持つクラス」の子が「子を持つクラス」である場合、子についてもう一度場合分けして考える。・・・②
②に分類される限り永遠に場合分けが続き、停止するのは①に分類される場合のみ。
循環継承がない限り、卑属の世代数は有限であるため、すべてのクラスは必ずいつか①に分類される。
循環継承がある場合、循環が起きているということは、すでに循環継承に関わるクラスにはすべてアクセス済みであるということである。
2-2.循環参照がそこにあるかの判定法
各クラスの親の1次元配列を考えよう。
このとき、各クラスの親もクラスであるため、各々の親の1次元配列を持っている。
そのため、各クラスは祖父母の2次元配列を持っているといえる。
同様に考えることで、一般に各クラスは直系尊属$n$親等の$n$次元配列を持っているということができる。
ここであるクラスを$c$と呼ぶこととする。$c$の先祖の任意の多次元配列に$c$が含まれることは、
$c$が循環継承しているということと同じである。
つまり命題「$c$の先祖配列 $\ni$ $c$ $⇔$ $c$は循環継承している」は真である。
この命題は次のように書き換えられる。
「$c$の先祖配列 $\ni$ $c'$ かつ$c'=c$ $⇔$ $c'$は循環継承している」
ここで「$c$の先祖配列 $\ni$ $c'$ 」とは、$c$が$c'$の子孫といえることと同じである。
$c'$からみて$c$の先祖配列とは、自身を含む先祖配列であり、その配列の少なくとも1つの元について、子孫に$c$を持つものである。
したがって、任意の「$c$を含む先祖配列」において、その元の少なくとも1つが子孫に$c'(=c)$を持つことと、$c'$が循環継承していることは同値だ。
ここで、「子孫に$d$を持つ任意のクラス$c$」の親クラスの先祖配列$P_1(c)$を考えよう。
$c$の任意の親を$p_1(c)$と呼ぶとき、$P_1(c)$は「$p_1(c)$を含む先祖配列」ということができる。
$P_1(c)$の元の少なくとも1つが子孫に$p_1(c)$を持つことと、$p_1(c)$が循環継承していることは同値である。
但し、子孫に$p_1(c)$を持つとき、必ず子孫に「$p_1(c)$の子孫」をも併せ持つ。つまり子孫として必ず$c$や$d$を持つというわけだ。
したがって、次のように言うことができる。
「子孫に$d$を持つクラス$c$の任意の親$p$が子孫に$d$を持つことと、$p$が循環継承していることは同値である」by 17ec084