この記事では、Alex MesoudiのRで書かれたチュートリアルをpythonに翻訳する。
下記の記事では間接バイアスのモデルが紹介されている。
文化的形質の伝達におけるバイアスは直接・内容バイアスと間接バイアスの二種類がある。前者は、文化形質がより記憶に残りやすい、発音しやすいなどの理由から他の文化形質と比べて伝達されやすい傾向のことを指し、後者は文化形質の持ち主の特性によって伝達されやすくなる傾向のことを指す。本稿では、後者をモデル化する
間接バイアスでは、学習者が、成功している・利得の高い実演者を優先的に模倣することによって、特定の形質がより継承される。下記では、利得バイアスをモデル化する。
エージェントベースシミュレーション
利得バイアス
まずは、必要なライブラリをインストールする。
import pandas as pd
import numpy as np
import random
import math
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib
コードは次のようになる。
def indirect_bias(N, s, p_0, t_max, r_max):
output = pd.DataFrame(np.tile(float('nan'), (t_max, r_max)))
output.columns = ["run_" + str(i) for i in range(r_max)]
for r in range(r_max):
agent = pd.DataFrame([random.choices(["A", "B"], k=N, weights=[p_0, 1 - p_0]), np.repeat(float('nan'), N)], index=["trait", "payoff"]).T
agent["payoff"][agent["trait"] == "A"] = 1 + s
agent["payoff"][agent["trait"] == "B"] = 1
output.iloc[0, r] = sum(agent["trait"] == "A") / N
for t in range(1, t_max):
previous_agent = agent.copy()
relative_payoffs = agent["payoff"].values / sum(agent["payoff"])
agent[["trait"]] = pd.DataFrame(random.choices(previous_agent["trait"], k=N, weights=relative_payoffs))
agent["payoff"][agent["trait"] == "A"] = 1 + s
agent["payoff"][agent["trait"] == "B"] = 1
output.iloc[t, r] = sum(agent["trait"] == "A") / N
plt.figure(figsize=(10, 5), dpi=100)
plt.plot(output)
plt.title(f'N = {N}, s = {s}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, t_max])
plt.ylim([0, 1])
plt.show()
実際に、シミュレーションしてみいる
indirect_bias(N = 10000, s = 0.1, p_0 = 0.01, t_max = 150, r_max = 5)
結果は、モデル3と非常によく似たものとなっている。
文化的ヒッチハイク
続いて、文化的ヒッチハイクをモデル化する。これは、機能的形質と中立的形質がある場合、中立的形質が機能的形質をヒッチハイクすることがあるというものである。コードは次のようになる。
def indirect_bias2(N, s, L, p_0, q_0, t_max, r_max):
output_trait1 = pd.DataFrame(np.tile(float('nan'), (t_max, r_max)))
output_trait2 = pd.DataFrame(np.tile(float('nan'), (t_max, r_max)))
output_trait1.columns = ["run_" + str(i) for i in range(r_max)]
output_trait2.columns = ["run_" + str(i) for i in range(r_max)]
for r in range(r_max):
agent = pd.DataFrame([random.choices(["A", "B"], k=N, weights=[p_0, 1 - p_0]), np.repeat(float('nan'), N), np.repeat(float('nan'), N)], index=["trait1", "trait2", "payoff"]).T
prob = np.random.rand(N)
agent["trait2"][np.logical_and(agent["trait1"] == "A", prob < L)] = "X"
agent["trait2"][np.logical_and(agent["trait1"] == "B", prob < L)] = "Y"
agent["trait2"][prob >= L] = random.choices(["X", "Y"], k=sum(prob >= L), weights=[q_0, 1 - q_0])
agent["payoff"][agent["trait1"] == "A"] = 1 + s
agent["payoff"][agent["trait1"] == "B"] = 1
output_trait1.iloc[0, r] = sum(agent["trait1"] == "A") / N
output_trait2.iloc[0, r] = sum(agent["trait2"] == "X") / N
for t in range(1, t_max):
previous_agent = agent.copy()
relative_payoffs = previous_agent["payoff"].values / sum(previous_agent["payoff"])
demonstrators = random.choices(range(N), k=N, weights = relative_payoffs)
agent[["trait1"]] = pd.DataFrame([previous_agent["trait1"][i] for i in demonstrators])
agent[["trait2"]] = pd.DataFrame([previous_agent["trait2"][i] for i in demonstrators])
agent["payoff"][agent["trait1"] == "A"] = 1 + s
agent["payoff"][agent["trait1"] == "B"] = 1
output_trait1.iloc[t, r] = sum(agent["trait1"] == "A") / N
output_trait2.iloc[t, r] = sum(agent["trait2"] == "X") / N
plt.figure(figsize=(10, 5), dpi=100)
plt.plot(output_trait1, label = "trait 1", color = "orange")
plt.plot(output_trait2, label = "trait 2", color = "#4169E1")
plt.title(f'N = {N}, s = {s}, L = {L}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, t_max])
plt.ylim([0, 1])
plt.legend()
plt.show()
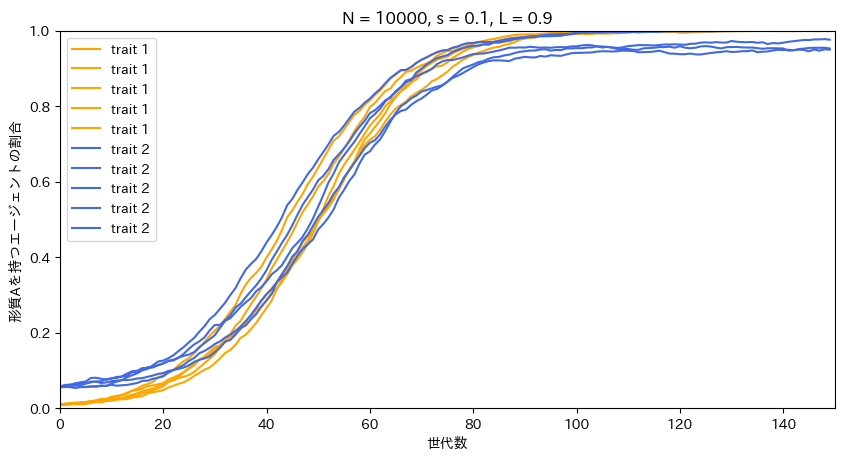
Lは二つの形質の結びつきの強さに関する変数である。Lが非常に高い値でシミュレーションしてみる。
indirect_bias2(N = 10000, s = 0.1, L = 0.9, p_0 = 0.01, q_0 = 0.5, t_max = 150, r_max = 5)
Lが0である場合についてシミュレーションしてみる。
indirect_bias2(N = 10000, s = 0.1, L = 0.0, p_0 = 0.01, q_0 = 0.5, t_max = 150, r_max = 5)
数値シミュレーション
数値シミュレーションの場合、次のようになる。
p′=\frac{p(1+s)}{p(1+s)+(1−p)} = \frac{p(1+s)}{1+sp} \
p = np.repeat(float(0), 150)
p[0] = 0.01
s = 0.1
for i in range(1,150):
p[i] = (p[i-1]*(1+s)) / (1 + (p[i-1])*s)
plt.figure(figsize=(10, 5), dpi=100)
plt.plot(p)
plt.title(f's = {s}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, 150])
plt.ylim([0, 1])
plt.show()