この記事では、Alex MesoudiのRで書かれたチュートリアルをpythonに翻訳する。
下記の記事ではバイアスのある・ない変異についてのモデルが紹介されている。突然変異(mutation)とは、ある形質が別の個体に継承される際に、別の形質へと変わることを意味する。
エージェントベースシミュレーション
まずは、必要なライブラリをインストールする。
python
import pandas as pd
import numpy as np
import random
import math
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib
バイアスのない突然変異
下記の記事で書いたコードを改変して、バイアスのない突然変異をモデル化してみる。
リスト同士の論理演算を行う場合、andを用いると後者の値をそのまま返し、orを用いると前者の値をそのまま返すというおかしな挙動をする。そのためリスト同士の論理演算を行う場合は、numpyのlogical_and()メソッドを用いる必要がある。
python
a = [True, False, False, True]
b = [True, True, False, False]
print(a and b)
#[True, True, False, False]
print(a or b)
#[True, False, False, True]
print(np.logical_and(a, b))
#[ True False False False]
python
previous_agent = agent.copy()
コードは下記のようになる。
python
def unbiased_mutation(N, mu,p_0, t_max, r_max):
output = pd.DataFrame(np.tile(float('nan'), (t_max, r_max)))
output.columns = ["run_" + str(i) for i in range(r_max)]
for r in range(r_max):
agent = pd.DataFrame(random.choices(["A", "B"], k=N, weights=[p_0, 1 - p_0]), columns = ["trait"])
output.iloc[0, r] = sum(agent["trait"] == "A") / N
for t in range(1, t_max):
previous_agent = agent.copy()
mutate = np.random.rand(N)
agent[np.logical_and(previous_agent["trait"] == "A", mutate < mu)] = "B"
agent[np.logical_and(previous_agent["trait"] == "B", mutate < mu)] = "A"
output.iloc[t, r] = sum(agent["trait"] == "A") / N
plt.figure(figsize=(10, 5), dpi=100)
plt.plot(output)
plt.title(f'N = {N}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, t_max])
plt.ylim([0, 1])
plt.show()
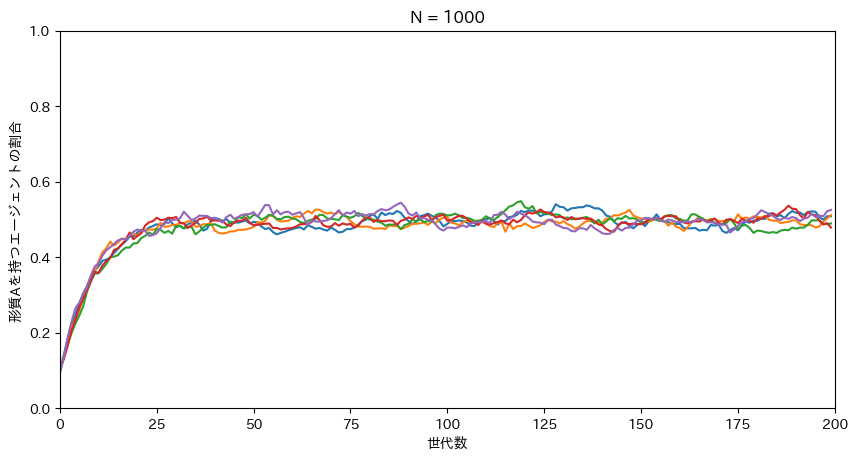
実際に、シミュレーションしてみる。p_0を0.1にすることで、形質Aを持つ個体が極めて少ない初期値にしているが、形質AとB両方が同じ割合に収束することが分かる。
python
unbiased_mutation(N=1000, mu = 0.05, p_0 = 0.1, t_max = 200, r_max = 5)
バイアスのある突然変異
続いて、バイアスのある突然変異をモデル化してみる。文化形質の場合、思い出しやすい形質へと変異することもある。
実装はAからBへ突然変異するコードを消せばよいので簡単にできる。
python
def biased_mutation(N, mu_b,p_0, t_max, r_max):
output = pd.DataFrame([[float('nan') for i in range(t_max)] for i in range(r_max)]).T
output.columns = ["run_" + str(i) for i in range(r_max)]
for r in range(r_max):
agent = pd.DataFrame(random.choices(["A", "B"], k=N, weights=[p_0, 1 - p_0]), columns = ["trait"])
output.iloc[0, r] = sum(agent["trait"] == "A") / N
for t in range(1, t_max):
previous_agent = agent.copy()
mutate = np.random.rand(N)
agent[np.logical_and(previous_agent["trait"] == "B", mutate < mu_b)] = "A"
output.iloc[t, r] = sum(agent["trait"] == "A") / N
plt.plot(output)
plt.title(f'N = {N}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, t_max])
plt.ylim([0, 1])
plt.show()
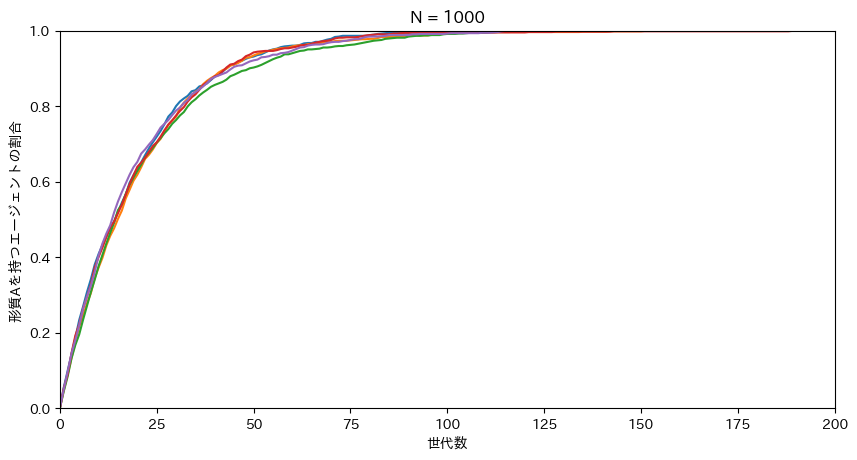
実際にシミュレーションしてみよう。100世代あたりで、形質Aが集団のすべてを占めていることが見て取れる。
python
biased_mutation(N = 100, mu_b = 0.05, p_0 = 0, t_max = 200, r_max = 5)
数値シミュレーション
数値シミュレーションの場合、次のようになる。
python
p_0 = 0
t_max = 200
mu = 0.1
p = np.repeat(float('nan'), t_max)
p[0] = p_0
for i in range(1,t_max):
p[i] = p[i-1]*(1-mu) + (1-p[i-1])*mu
plt.figure(figsize=(10, 5), dpi=100)
plt.plot(p)
plt.title(f's = {s}')
plt.xlabel('世代数')
plt.ylabel("形質Aを持つエージェントの割合")
plt.xlim([0, 150])
plt.ylim([0, 1])
plt.show()
