準備
Andrej Karpathy
元Tesla社AI部部長・Autopilotプロジェクト開発リーダー
OpenAI創設者メンバーの一人、現在OpenAI所属
この記事はAndrej Karpathy氏の動画:
The spelled-out intro to neural networks and backpropagation: building micrograd
を日本語翻訳したものです。この動画はPyTorchやNumPyなどのニューラルネットワークライブラリーを使わずmathのみで $0$ から基本的なニューラルネットワーク(今回はパーセプトロン)の演算ができるものを作ってみようといった趣旨の動画です。
なるべくわかりやすいように書いていきますが、量が多く流れが不自然なところがあると思うのでぜひコメントのほうでフィードバックしていただけると助かります。
使用するもの
jupyter (notebook, lab どっちもOK)
使用ライブラリ
- math
- numpy # 例題で使用
- matplotlib
- graphviz
graphviz パッケージは graphviz のバイナリーをインストールする必要があります。
(Arch) $ sudo pacman -S graphviz
(Windows) $ https://www.graphviz.org/download/
1. Pythonの基本的な演算の仕方
import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
まずは簡単な演算を行ってみましょう。そうするためにいくつかのライブラリーをインポートします。
numpyは数値計算を効率的に行うためのライブラリー(拡張モジュール)です。
まずは数式 $3x^{2}-4x+5$ 計算してくれる関数をPython上で作ってみましょう。
def f(x):
return (3 * (x ** 2)) - (4 * x) + 5
f(3.0) # jupyterではprintなしで値の出力ができる
# 出力 ####
# 20.0
グラフ化するために、まずいっぱい $x$ を作りたいです。numpyのnp.arange()関数を使うと連続する数を生成できます。まずは -5 から 5 まで、0.25 間隔に生成してみましょう。
xs = np.arange(-5, 5, 0.25)
xs
# 出力 ####
# array([-5. , -4.75, -4.5 , -4.25, -4. , -3.75, -3.5 , -3.25, -3. ,
# -2.75, -2.5 , -2.25, -2. , -1.75, -1.5 , -1.25, -1. , -0.75,
# -0.5 , -0.25, 0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 ,
# 1.75, 2. , 2.25, 2.5 , 2.75, 3. , 3.25, 3.5 , 3.75,
# 4. , 4.25, 4.5 , 4.75])
$y=f(x)$ になるようにして作った $xs$ を入れてみましょう。インポートしたmatplotlibを使うとグラフが描けるようになります。plt.plot(x軸, y軸) といった使い方です。
xs = np.arange(-5, 5, 0.25)
ys = f(xs)
plt.plot(xs, ys)
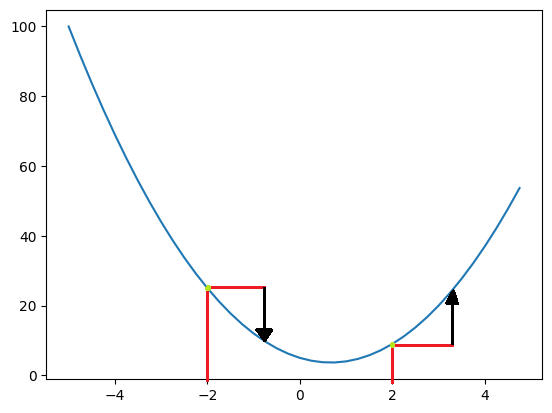
グラフが生成されました。ちょっとこの図を見てみましょう。
ある関数のグラフを書いたとき、「あるところのグラフの傾き」を求めるにはどうすればいいでしょう?
例えば、「あるところ」が $x = 2$ のとき、グラフ上では紫の点のところを意味します。
ここでは明らかに次(例えば $x=2.1$)に進むにつれてグラフがどんどん上に上昇するのがわかります。逆に $x=-2$ で同じことを考えると $0$ ちょっとすぎたところに向かってグラフが下のほうに降下していくのがわかります。
つまり傾きを求めるということは
「あるところからちょっと進んだとき、グラフが上に行くのか下に行くのかを考える」 ということに等しいです。図を見てみましょう。
ある地点からちょっと進んでグラフがある方向に向かう、これが傾きを求めるプロセスの本質です。
このまま言葉通りの傾きを描いてみると次のようになります。
(ちょっと見づらいのですが、紫の線です。)
なるほど、傾きってそんなものかとなってもらえればと思います。
それで、「傾きなんか求めてどうするの?」 と思うかもしれませんが、ニューラルネットワークを構築するにあたって前提知識として必要です。後ほど めっちゃ使います 。覚えておきましょう。
まずはこの傾きを求めるプロセスを数式化してみましょう。「ちょっと進んだ」ってのを足し算で表して、ほんの少しだけ動いたとしましょう。
h = 0.1
x = 2
print( f(x) )
print( f(x + h) )
print( f(x + h) - f(x) )
print( (f(x + h) - f(x)) / h )
# 出力 ####
# 9
# 9.83
# 0.8300000000000001
# 8.3
4つの print() 文がありますが、一つずつ見ていきましょう。
1番目は作った関数の $x=2$ 地点でのグラフ上の値です。
2番目は $f(x + h)$、$x$ から $h$ だけ進んだときのグラフ上の値です。
3番目は 1番目から2番目になったときどれだけ動いたか、差をとったものです。
4番目はなんでしょう?求めた差を進んだ分で割っています。こうすると、わかることは
「$0.1$ だけ進んだとき、グラフ上の点が上下にどれだけ動くか?」 がわかりますね。
今の場合、 $8.3$ なので上方向に $8.3$ だけ動いたのがわかります。
Wikipediaに乗っているある式なんですが、私たちが今作った式と同じです。そう、これが高校数学で学ぶ、微分 の定義です。$h$ をどんどん小さくすることで、さらに高精度のグラフの微分を求める(傾きを求める)ことができます。
次に、もうちょっと発展したものを書いてみましょう。やり方は同じです。
h = 0.00001
a = 2.0
b = -3.0
c = 10.0
d = a * b + c
e = c + h
f = a * b + e
print(d)
print(f)
print((f - d) / h)
# 出力 ####
# 4.0
# 4.00001
# 0.9999999999621422
$a, b, c, e$ から成る二つの関数 $d, f$ を作ってみました。$e$ は $c$ に $h$ だけ足したもので、$f$ に $c$ の代わりに $e$ を足したものとなっています。
次に、これらの値をニューラルネットワークのノードとして扱えるようにいろんなものが集まったクラスを定義して値を入れちゃいましょう。
class Value:
# オブジェクト宣言時の初期化、initializer
def __init__(self, _data, _prev = (), _op = '', _label = ''):
self.data = _data # ノードが持つデータ
self.grad = 0.0 # ノードが持つ勾配(傾き)
self.prev = set(_prev) # 演算前のノード
self.op = _op # 演算子
self.label = _label # 出力用ラベル
# 出力、representation
def __repr__(self):
return f"Value(data={self.data})"
# 足し算、addition(+)
def __add__(self, other):
result = Value(self.data + other.data, (self, other), '+')
return result
# 掛け算、multiplication(*)
def __mul__(self, other):
result = Value(self.data * other.data, (self, other), '*')
return result
これで数字1個だけでなく、Valueをデータ型として使っていろんなものを詰め込めるようになりました。
Valueのdataには上で定義した $a, b, c, d, e, f$ のような値を代入するもの、
grad は後ほど使いますが、ノードの傾きを入れておくもの、
prev は今のノードがほかのノードたちとの演算によるものだとするとき、それらのノードたちがどれなのかを示す(例えば子供には必ず親がいるように)もの、
op はどの演算子で今のノードができたのかを示すものです。
labelは名前付け用のラベルです。
__repr__ や __add__ などはPython上で予約されているキーワードです。例えば __add__ は + 演算子がどのような振る舞いをするかをユーザーが再定義できるようにするものです。ここでは単純に新しい Value型変数を作って中身にデータを詰め込んで返しているだけです。
prevとopはちょっと紛らわしいのですが、例文でちょっとやってみましょう。
a = Value( 2.0, _label = 'a')
b = Value(-3.0, _label = 'b')
c = a * b; c.label = 'c'
d = Value(10.0, _label = 'd')
# a + b -> a.__add__(b)
# a * b -> a.__mul__(b)
print("a + b", a + b, a.prev, b.prev)
print("a * b", a * b, a.prev, b.prev)
# 出力 ####
# a + b Value(data=-1.0) set() set()
# a * b Value(data=-6.0) set() set()
Valueデータ型として $a, b, c, d$ を宣言して、値を代入しました。
ここから本格的にニューラルネットワークを作りますが、その前にニューラルネットワークが学習するとき使う方法の一つである「逆伝搬」というものを手書きでちょっとだけ練習してみたいと思います。
e = c + d; e.label = 'e'
print("e", e, e.prev, e.op)
f = Value(-2.0, _label = 'f')
print("f", f, f.prev, f.op)
# 最後のノード、損失関数(Loss function)
L = e * f; L.label = 'L'
# 逆伝播の練習のために、Lの勾配を任意に設定
L.grad = 1.0
# 出力 ####
# e Value(data=4.0) {Value(data=10.0), Value(data=-6.0)} +
# f Value(data=-2.0) set()
あらゆる演算をした最後に損失を出力するノードL $L$ を定義しました。
「急に損失って何の話や」と思ったかもしれません。ニューラルネットワークの最終目的は、予測の誤りをできるだけ減らすことです。たとえば、リンゴの写真をニューラルネットに見せた時、「これはリンゴだ」ではなく「これはリンゴであろう」と予測します。その予測がどれだけ正確かを数値化し、それに対してエラー率を可能な限り減らすことが目的です。
今の「損失 $L$」は、まだニューラルネットワークを作ったわけではありませんが、逆伝搬の練習として損失関数としてみてみようって感じです。
それではこの $L$ をいい感じに出力するために、グラフ化する処理を書いてみましょう。
次のコードは本記事の内容と全く関係がないので、コピペでかまいません。内容は省きます。
from graphviz import Digraph
def trace(root):
nodes, edges = set(), set()
def build(verticies):
if verticies not in nodes:
nodes.add(verticies)
for child in verticies.prev:
edges.add((child, verticies))
build(child)
build(root)
return nodes, edges
def draw_dot(root):
dot = Digraph(format = 'svg', graph_attr = {'rankdir': 'LR'}) # LR = Left to Right
nodes, edges = trace(root)
for node in nodes:
uid = str(id(node))
dot.node(name = uid, label = "{ %s | %.4f | grad(%.4f) }" % (node.label, node.data, node.grad), shape = 'record')
if node.op:
dot.node(name = uid + node.op, label = node.op)
dot.edge(uid + node.op, uid)
for node1, node2 in edges:
dot.edge(str(id(node1)), str(id(node2)) + node2.op)
return dot
draw_dot(L) # グラフを出力
図のように、$L$ にたどり着くまでの演算がいい感じに出力されました。
ここから逆伝搬の実践です。
2. 手書きで逆伝播
まず $L$ は $L = e \times f$ なので $\frac{d(L)}{d(e)} = f$ になります。なぜそうなるかというと
上で習った微分の定義は $\lim_{h \to +\infty}\frac{f(x+h) - f(x)}{h}$ なので
( $\lim$ に慣れていない方は無視しても構いません。)
$\lim_{h \to +\infty}\frac{((e + h) \times f) - (e \times e)}{h}$ これを展開すると
$\lim_{h \to +\infty}\frac{(e \times f) + (h \times f) - (e \times f)}{h}$ になり $(e \times f)$ は ± で消えます。
ここで $\frac{h}{h}=1$ なので $\lim_{h \to +\infty}\frac{h \times f}{h} = 1 \times f$ になります。
これは $\frac{d(L)}{d(e)} = f$ と同じです。
$e$ と $f$ の傾きの求め方がわかったので手打ちで入れてみましょう。
e.grad = -2.0 # e.grad = d(L)/d(e) = f
f.grad = 4.0 # f.grad = d(L)/d(f) = e
# 上で求めた値があってるか確認するための適当な関数
def temp():
# 変化率
h = 0.0001
# 上で書いたコードを適当にコピペ
a = Value( 2.0, _label = 'a')
b = Value(-3.0, _label = 'b')
c = a * b; c.label = 'c'
d = Value(10.0, _label = 'd')
e = c + d; e.label = 'e'
f = Value(-2.0, _label = 'f')
L = e * f; L.label = 'L'
L1 = L.data
a = Value( 2.0, _label = 'a')
b = Value(-3.0, _label = 'b')
c = a * b; c.label = 'c'
d = Value(10.0, _label = 'd')
e = c + d; e.label = 'e'
f = Value(-2.0 + h, _label = 'f') # h に注目
L = e * f; L.label = 'L'
L2 = L.data
grad = (L2 - L1) / h # f の勾配(傾き) = 4.0
print(grad)
temp() # temp() 関数を呼び出して出力
# 出力 ####
# 3.9999999999995595
$f$ の勾配(傾き、ここからは勾配といいます)である $4$ が出力されました。
引き続き $L$ に対する $c$ と $d$ の勾配を求めてみましょう。
ここからは連鎖則(チェーンルール)を使ってみましょう。例えば
「車 ($z$) が自転車 ($y$) より2倍早く、自転車 ($y$) が歩き ($x$) より4倍早い」
とするとき、「車」と「歩き」は間に「速さ」としての関係性があるため、次のように表せます。
$\frac{d(z)}{d(x)}=\frac{d(z)}{d(y)}\frac{d(y)}{d(x)}=2 \times 4=8$
なので車は歩きより8倍早いことがわかりますね。この例と同様に $d$ を解くと次のようになります。
$\frac{d(L)}{d(d)}=\frac{d(L)}{d(e)}\frac{d(e)}{d(c)}=-2.0 \times 1.0=-2.0$
同様に $a, b, c$ も求めてみましょう。
下に解答が載っていますが、まずここで止めて自分で求めてみてください!
c.grad = -2.0
d.grad = -2.0
a.grad = -2.0 * -3.0
b.grad = -2.0 * 2.0
draw_dot(L) # グラフを出力
これでグラフが全部埋められました。検算してもあってることがわかりますね。
ラストステップに、次のコードがどのように出力されるか考えてみましょう!
解答は載っていないのでJupyterにコードを書いて確認してみてください。
# 親ノードを持たない者同士にデータに勾配をかけてみる
a.data = a.data + (0.01 * a.grad)
b.data = b.data + (0.01 * b.grad)
d.data = d.data + (0.01 * d.grad)
f.data = f.data + (0.01 * f.grad)
c = a * b
e = c + d
L = e * f
print(L.data)
# 出力 ####
# ???
3. 簡単なニューラルネットワークを設計してみる
いよいよニューラルネットワークを作る段階に来ました。
まずはニューロンって何なのかをちょっと話してから次に行きましょう。
ニューロンとは、私や皆さんの脳内を構成する、脳細胞に当たるものです。それらが何億個も集まり、お互いつながって脳になっています。ニューロン細胞の核 (nucleus) を中心に、樹状の突起 (dendrite) がいっぱい生えていて、ほかのニューロンからの信号を受け入れるようになっています。そして軸索 (axon) から信号を出す形です。軸索は長く伸びていて末端にカエルの足のように伸びた軸索末端 (axon terminal) がほかのニューロンのデンドライトにくっついて電気信号を受送信している感じです。その軸索末端のさらに先端の突起をシナプス (synapse) と呼びます。シナプスはニューロンごとに1000個から10000個程度あり、一つのニューロンに複数のニューロンからの入力信号が入ってくるのが普通です。
人間の脳はこのようなニューロンが860億±80億個あるようです。しかし、ほかのニューロンと通信を行うシナプスの数は定かではなく、おそらくは100兆~1000兆個以上あるのではないか?といわれています。
最近chatGPTでお馴染みのGPT4の場合、170兆個のシナプス(パラメータ)を持っていると言われています。大体人間の脳の1/10といったところでしょうか。
それではこのニューロンを数式化してみましょう。
ほかのニューロンから軸索を通じて入ってきた入力を $x_0$, そしてシナプス自身が持つ信号を重み (weight) と呼び $w_0$, それらを掛け合わせたものを加重和 (weighted sum) と呼びほかのニューロンに入る形です。このようにして計算されたいくつかの加重和を全部足し合わせてこのニューロンが反応するべきかを判断します。この判断を行う作業を関数として作って、活性化関数と呼びます。急に活性化関数とか言い出して難しい雰囲気になりますが、やってることは結構簡単です。「加重和を全部足し合わせた何かの値が一定値を超えてれば発火するよ」くらいの話です。
今の話をまとめると:
- 人間の脳は1000億個くらいのニューロンを持っていて
- ニューロンは1000個くらいのシナプスを持っていて
- それらシナプスを使って複数のニューロンと結合して通信!
これを数式化して:
- ニューロン1個を $y$ とすると
- ほかのニューロンから入る入力 $x_n$ があって
- シナプスが持つ重みを入力にかけてやると加重和になる $x_n \times w_n $
- 入力が複数個って言ったから全部足しちゃおう $\sum_{i} x_{i}w_{i} = g$
- 足し合わせたものを活性化関数 $f$ に入れる! $f(g)$
- それがニューロンが出す出力になるよね $f(g) = y$
って感じです。
それでは、ニューラルネットワークのために Value クラスを拡張しましょう。
class Value:
def __init__(self, data, _children=(), _op='', _label = ''):
self.data = data
self.grad = 0
self.prev = set(_children)
self.op = _op
self.label = _label
+ self._backward = lambda: None
def __repr__(self):
return f"Value(data={self.data}, grad={self.grad})"
def __add__(self, other):
+ other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data, (self, other), '+')
return out
def __mul__(self, other):
+ other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
return out
+ def __pow__(self, other): # self ^ other
+ assert isinstance(other, (int, float)), "only supporting int/float powers for now"
+ out = Value(self.data**other, (self,), f'**{other}')
+ return out
+
+ def __neg__(self): # -self
+ return self * -1
+
+ def __radd__(self, other): # other + self
+ return self + other
+
+ def __sub__(self, other): # self - other
+ return self + (-other)
+
+ def __rsub__(self, other): # other - self
+ return other + (-self)
+
+ def __rmul__(self, other): # other * self
+ return self * other
+
+ def __truediv__(self, other): # self / other
+ return self * other**-1
+
+ def __rtruediv__(self, other): # other / self
+ return other * self**-1
一つずつ見ていきましょう。
まず既存の __add__() __mul__() に1行追加されました。これは、+ と * 演算を行うとき、二つの数がValue型であるかをチェックします。例えば次のような状況:
a = Value( 2.0, _label = 'a')
b = Value( -3.0, _label = 'b')
a + b # 問題なし
a + -3 # -3って何型?
ここで、ただの数字と演算を行うときこの $-3$ を Value 型に変換する作業を行うことで問題なく + や * ができるようにしているのです。
新しく追加された __pow__() などはコード内コメントにどのような動作をするか書いておきました。
一つ注目するべきものは、割り算 __truddiv__() の場合、Pythonでは基本的に割り算を行うものが存在しないので代わりに __pow__() を用いて逆数をかけることで割り算を行っています。
$other^{-1}$ は $\frac{1}{other}$ と同じです。
それでは簡単な式をコードにして書いてみましょう。
# 入力
x1 = Value(2.0, _label='x1')
x2 = Value(0.0, _label='x2')
# 重み
w1 = Value(-3.0, _label='w1')
w2 = Value( 1.0, _label='w2')
# バイアス、後ほど説明します
b = Value(6.8813735870195432, _label='b')
# 加重和
x1w1 = x1*w1; x1w1.label = 'x1w1'
x2w2 = x2*w2; x2w2.label = 'x2w2'
# 加重和の足し合わせ
wsum = x1w1 + x2w2; wsum.label = 'wsum'
# バイアスも加える
g = wsum + b; g.label = 'g'
draw_dot(g)
バイアスについては、後ほどまた説明したいと思います。今は「この値を基準に活性化するかしないかを決める」くらいのものだと考えましょう。
次に活性化関数について考えてみます。
x = np.arange(-5, 5, 0.2)
y = np.tanh(x) # 今回使う活性化関数、tanh()
plt.plot(x, y); plt.grid();
加重和を全部足し合わせたものをこの関数に入れると、$-4$ 以下の場合は出力として $y = -1$ を、$4$ 以上の場合は出力として $y = 1$ を出力してその間の区間ではとても滑らかに値を調整しているのがわかると思います。入ってきた入力から $-1$ ~ $1$ の値に圧縮して、これが一定値を超えると発火(活性化)する感じです。
$\tanh$ 関数とその勾配は次のように定義されます。
$$\tanh{x} = \frac{\sinh{x}}{\cosh{x}} = \frac{e^{2x} - 1}{e^{2x} + 1} \quad\quad \tanh'{x}=1-\tanh^{2}{x}$$
これをValueクラス内に定義します。
def __pow__(self, other): # self ^ other
...
+
+ def tanh(self):
+ x = self.data
+ t = ((math.exp(2 * x) - 1) / (math.exp(2 * x) + 1))
+ out = Value(t, (self, ), 'tanh')
+ return out
+
def __neg__(self): # -self
...
それでは先作った例題に適用してみましょう。
# 入力
x1 = Value(2.0, _label='x1')
x2 = Value(0.0, _label='x2')
# 重み
w1 = Value(-3.0, _label='w1')
w2 = Value( 1.0, _label='w2')
# バイアス、後ほど説明します
b = Value(6.8813735870195432, _label='b')
# 加重和
x1w1 = x1*w1; x1w1.label = 'x1w1'
x2w2 = x2*w2; x2w2.label = 'x2w2'
# 加重和の足し合わせ
wsum = x1w1 + x2w2; wsum.label = 'wsum'
# バイアスも加える
g = wsum + b; g.label = 'g'
+ y = g.tanh();
+ draw_dot(y)
ここで、逆伝搬をちょっとやってみましょう。
y.grad = 1.0
# y = tanh(g)
# dy/dg = 1 - tanh(g)^2 = 1 - y^2
1 - y.data**2
# 出力 ####
# 0.49999999999
なんと、ぴったり $0.5$ が出ました。そう、バイアスの数字の羅列は勾配の値をきれいにするためにそのような数字にしただけで、特に意味はありません。「じゃあ結局バイアスってなんやねん」となりますがもうちょっと待ってください。まずは逆伝搬を終わらせましょう。
次は $b$ と $wsum$ の勾配を求めます。+ 演算の場合、その微分は $1$ なので $1$ をかけて $0.5$ になるようなもの、つまり $0.5$ そのものです。連続に $x1w1$ と $x2w2$ も $0.5$ です。
g.grad = 0.5
b.grad = 0.5
wsum.grad = 0.5
x1w1.grad = 0.5
x2w2.grad = 0.5
続けて、$x1$, $x2$, $w1$, $w2$ の勾配も求めてみましょう。
x1.grad = w1.data * x1w1.grad
w1.grad = x1.data * x1w1.grad
x2.grad = w2.data * x2w2.grad
w2.grad = x2.data * x2w2.grad
これで逆伝搬が完了です。
さて、逆伝搬を手書きでやるのはかなりの量のコードを消費し、面倒くさいプロセスであることがわかりました。ここからはこれを自動化してみます。先ほど拡張した Value クラスのイニシャライザーの中に、こういうものがありました。
class Value:
def __init__(self, data, _children=(), _op='', _label = ''):
self.data = data
self.grad = 0
self.prev = set(_children)
self.op = _op
self.label = _label
+ self.backward = lambda: None
_backward にこのノードがどのような逆伝搬をすればいいかを入れます。まずは + に対しての逆伝搬を考えてみましょう。+ の場合、自分自身の勾配は出力後のノードの勾配と同じ、あるいは $1$ をかけたものでした。なので次のようなコードになります。
def __add__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data, (self, other), '+')
+ def _backward():
+ self.grad = self.grad + (1 * out.grad)
+ other.grad = other.grad + (1 * out.grad)
+ out._backward = _backward
+
return out
続けて、* の場合についても考えてみます。self と other を掛け合わせる場合、self の勾配は other のデータと次のノードの勾配の積でした。なので次のように表せます。
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
+ def _backward():
+ self.grad = self.grad + (other.data * out.grad)
+ other.grad = other.grad + (self.data * out.grad)
+ out._backward = _backward
+
return out
さらに、累乗と $\tanh$ も勾配式を書きましょう。累乗の勾配は $(m^{k})'=km^{k-1}$ で $\tanh$ の勾配はすでに説明したのでコードにすると次のようになります。
def __pow__(self, other):
assert isinstance(other, (int, float)), "only supporting int/float powers for now"
out = Value(self.data**other, (self,), f'**{other}')
+ def _backward():
+ self.grad = self.grad + ((other * self.data**(other - 1)) * out.grad)
+ out._backward = _backward
+
return out
def tanh(self):
x = self.data
t = ((math.exp(2 * x) - 1) / (math.exp(2 * x) + 1))
out = Value(t, (self, ), 'tanh')
+ def _backward():
+ self.grad = (1 - t**2) * out.grad
+ out._backward = _backward
+
return out
これでいちいち値を代入することなく、関数を呼び出すだけで逆伝搬ができるようになりました。やってみましょう。
- g.grad = 0.5
- b.grad = 0.5
- wsum.grad = 0.5
- x1w1.grad = 0.5
- x2w2.grad = 0.5
- x1.grad = w1.data * x1w1.grad
- w1.grad = x1.data * x1w1.grad
- x2.grad = w2.data * x2w2.grad
- w2.grad = x2.data * x2w2.grad
+ g._backward()
+ b._backward()
+ wsum._backward()
+ x1w1._backward()
+ x2w2._backward()
+ x1._backward()
+ w1._backward()
+ x2._backward()
+ w2._backward()
でもまだ関数を一個一個呼び出さないといけないので、自動化します。
def tanh(self):
...
+ def backward(self):
+ topo = []
+ visited = set()
+
+ def build_topo(v):
+ if v not in visited:
+ visited.add(v)
+
+ for child in v.prev:
+ build_topo(child)
+ topo.append(v)
+
+ build_topo(self)
+ self.grad = 1.0
+
+ for node in reversed(topo):
+ node._backward()
def __neg__(self):
...
これで backward() を呼び出すだけですべてのノードにおいて逆伝搬ができるようになりました。
- g._backward()
- b._backward()
- wsum._backward()
- x1w1._backward()
- x2w2._backward()
- x1._backward()
- w1._backward()
- x2._backward()
- w2._backward()
+ y.backward()
+ draw_dot(y)
逆伝搬の実装が終わったので、簡単なニューラルネットワークのパーセプトロンを作ってみましょう。新しいクラス Neuron を作ります。
import random
class Neuron:
def __init__(self, n_input):
self.w = [Value(random.uniform(-1, 1)) for _ in range(n_input)]
self.b = Value(random.uniform(-1, 1))
def __call__(self, x):
act = sum(wi * xi for wi, xi in zip(self.w, x)) + self.b
out = act.tanh()
return out
x = [2.0, 3.0]
n = Neuron(2) # __init__呼び出し
n(x) # __call__呼び出し
# 出力 ####
# Value(data=-0.9973169191388699, grad=0)
出力はランダムなので、私の結果と異なる値が出ると思います。クラス内部の w は $-1$ ~ $1$ の範囲でランダムな値を持ち、n_input の数だけ生成されます。__call__ が呼び出されると、self.w と x をそれぞれ wi, xi として展開し、その値を乗算した結果 wi * xi を sum() 関数で全て合算します。最後に、バイアスを加えて tanh() 関数を適用することで出力が完成します。
次は階層(レイヤー)を実装します。新しく Layer クラスを定義します。
class Layer:
def __init__(self, n_input, n_outs):
self.neurons = [Neuron(n_input) for _ in range(n_outs)]
def __call__(self, x):
outs = [n(x) for n in self.neurons]
return outs[0] if len(outs) == 1 else outs
x = [2.0, 3.0]
l = Layer(2, 3)
l(x)
# 出力 ####
# [Value(data=-0.3889254542303636, grad=0),
# Value(data=-0.860026311032568, grad=0),
# Value(data=-0.5455552647311676, grad=0)]
さっきの例題とは違って、Layer クラスはイニシャライザーで Neuron 型オブジェクトを持っています。n_output の数だけニューロンを作ります。同じく配列です。
次は MLP (Multi-Layer Perceptron)クラスを実装します。
class MLP:
def __init__(self, n_input, n_outs):
sz = [n_input] + n_outs
self.layers = [Layer(sz[i], sz[i + 1]) for i in range(len(n_outs))]
def __call__(self, x):
for layer in self.layers:
x = layer(x)
return x
x = [2.0, 3.0, -1.0]
mlp = MLP(3, [4, 4, 1])
mlp(x)
# 出力 ####
# Value(data=-0.8223839367226711, grad=0)
図を見てみましょう。
白い丸が Neuron クラス、そして Layer クラスで各々のレイヤーを実装しています。そして MLP クラスで大きさ $3-4-4-1$ のパーセプトロンを実装している感じです。
それでは例題を見てみましょう。
xs = [
[2.0, 3.0, -1.0],
[3.0, -1.0, 0.5],
[0.5, 1.0, 1.0],
[1.0, 1.0, -1.0],
]
ys = [1.0, -1.0, -1.0, 1.0] # 教師信号、ニューラルネットワークの出力がこれらの値になってほしい
y_prediction = [n(x) for x in xs]
y_prediction
# 出力 ####
# [Value(data=0.6495332522972835, grad=0),
# Value(data=0.5337599260349284, grad=0),
# Value(data=0.24434824868505903, grad=0),
# Value(data=0.6960478730892988, grad=0)]
それではこれらの値が「どれだけ正解(ys)から離れているか」、つまり誤差を求めたいと思います。誤差を求める手法はいくつかありますが、ここでは二乗誤差を使います。
loss = sum((y_out - y_ground)**2 for y_ground, y_out in zip(ys, y_prediction))
loss
# 出力 ####
# Value(data=4.116035911415101, grad=0)
二乗誤差は現在の出力 y_out から正解 y_ground を引いて、それを二乗したものです。今は誤差が $4$ で結構正解から離れていますが、私たちのニューラルネットワークの目的はこの誤差を $0$ に 近づけるす ることです。ここで、逆伝搬を使って誤差を減らしていきます。
loss.backward()
print(mlp.layers[0].neurons[0].w[0].grad)
draw_dot(loss)
# 出力 ####
# -0.6455390402326302
ニューラルネットワーク内のパラメータを一個取り出してみました。全部取り出してみたいですね。それと一緒にグラフを書いてみましたが、ご覧の通り、ニューラルネットワークの逆伝搬を私たちの手でいちいち書いていくことは無駄だってわかる大きさですね。それではパラメータを全部出力してくれる関数を実装しましょう。次のコードを各クラスに追加してください。
class Neuron:
...
def parameters(self):
return self.w + [self.b]
class Layer:
...
def parameters(self):
return [p for neuron in self.neurons for p in neuron.parameters()]
class MLP:
...
def parameters(self):
return [p for layer in self.layers for p in layer.parameters()]
この parameters() を使って出力します。
mlp.parameters()
# 出力 ####
#[Value(data=-0.30912159636672865, grad=0),
# Value(data=-0.6603149589582724, grad=0),
# Value(data=-0.5319976029474467, grad=0),
# Value(data=0.8896261930830782, grad=0),
# Value(data=-0.34701856284798094, grad=0),
# Value(data=-0.5300517249405299, grad=0),
# Value(data=-0.7170680573953743, grad=0),
# Value(data=-0.9870674738622613, grad=0),
# Value(data=0.31587379858620923, grad=0),
# Value(data=0.3633914945950387, grad=0),
# Value(data=0.365198650910316, grad=0),
# Value(data=-0.9673199425947787, grad=0),
# Value(data=-0.07494953519076653, grad=0),
# Value(data=-0.7896444404505285, grad=0),
# Value(data=-0.2910685459891216, grad=0),
# Value(data=-0.5492522767004173, grad=0),
# Value(data=0.5761046676832269, grad=0),
# Value(data=-0.9022678930849077, grad=0),
# Value(data=-0.07738281804494429, grad=0),
# Value(data=0.120685124222492, grad=0),
# Value(data=0.8883445722373418, grad=0),
# Value(data=0.9587703547092226, grad=0),
# Value(data=0.6115783207311509, grad=0),
# Value(data=-0.48137158620674225, grad=0),
# Value(data=-0.5917815656907703, grad=0),
...
行が多いため省略表示されていますが、これらがネットワーク内のすべての重みとバイアスです。これら重みやバイアスを全部まとめてパラメータと呼びます。ニューラルネットワークは、これらパラメータをある「誤差率を減らせる」値に「近づける」ことで私たちの目的である、ニューラルネットワークの 学習 を実現できるわけです。
ここまでの内容をまとめてみましょう。
- ニューラルネットワークの目的は、学習を通じてあるゴールの値(教師信号など)に近づけるのが目的
- ニューラルネットワークは誤差率を0に近づける必要がある。
- 2を満足させるプロセスを学習と呼ぶ。
- ニューラルネットワーク内には重みとバイアス群があり、これらをまとめてパラメータと呼ぶ。
- 誤差率が0に近づくようなパラメータの値にすることが学習である。
といった感じでしょうか。
ここからは学習を実装してみましょう。今回の記事では逆伝搬を使って学習します。その逆伝搬の自動化も終わったので、残ったのは誤差率が0にある程度近づくまで逆伝搬を繰り返すだけです。
for k in range(30):
y_prediction = [mlp(x) for x in xs]
loss = sum((y_out - y_ground)**2 for y_ground, y_out in zip(ys, y_prediction))
for p in mlp.parameters():
p.grad = 0.0
loss.backward()
for p in mlp.parameters():
p.data += -0.05 * p.grad
print(k, loss.data)
# 出力 ####
# 0 6.786896795558372
# 1 5.604540707189145
# 2 3.512068063950318
# 3 2.8963876719258836
# 4 2.3504413594558597
# 5 1.8438610835711329
# 6 1.3726215932366406
# 7 0.9770347524991135
# 8 0.6898071396635169
# 9 0.5009076459907377
# 10 0.3790797418884145
# ...
# 26 0.05632626891125439
# 27 0.05305464602317643
# 28 0.050114263954451926
# 29 0.04745876590127526
これで学習が自動的に進み、誤差率が $0.05$ 未満になるまで繰り返しているのが見えますね。ここで、ニューラルネットワークが学習を経て最初の目標値であった $ys$ とどこまで近くなったか見てみます。
ys
y_prediction # この2行はjupyter内に分割して入れてください
# 出力
# [1.0, -1.0, -1.0, 1.0]
#
# [Value(data=0.907718193665716, grad=-0.1845636126685679),
# Value(data=-0.9542142611252579, grad=0.09157147774948426),
# Value(data=-0.8570035942553672, grad=0.2859928114892656),
# Value(data=0.8719432618689386, grad=-0.2561134762621229)]
注目するべきところは data=のところです。うーん、まだちょっと微妙に離れていますが、学習がもっと進めばいい感じになると思います。
私たちがここでやったように、あるゴールに向かってボールが転がるように学習を進める方法を 勾配降下法(Gradient Descent) と呼びます。誤差というものはあるところでは高く、ある一定のところで私たちが求めている値と合致すると低くなると考えてみましょう。それをグラフにマッピングしてみると次のようになります。
(出典:MIT OCW 6.S191)
これはすべての重み空間においてばらつきのある誤差を地形図のようにマッピングしたものです。これを誤差風景(Loss landscape)とも呼びます。図の真ん中の青いところが私たちが求めている値が存在するところで、そこにボールが転がってはまったのが学習成功のときです。
4. 終わりに
まだ記事がちょっと不安定です!
このセクションは記事の作成が完全に終わったら消します。
やるべきこと
- パーセプトロンの説明
- バイアスの説明
- 学習率の説明
- 日本語がやばい
- 流れの改善