はじめに
機械学習でクラス分類を行う際、クラス分類結果と同時に、それらのクラスに属する確率も得たいときがあります。
正例のデータ数が負例のデータ数に比べて極端に少ない場合(このようなデータを不均衡データと呼びます)、それらのデータをすべて用いて予測モデルを構築すると、予測結果も負例となることが多く、正例のデータを精度よく分類することが難しくなる傾向があります。そこで、負例のデータ数が正例のデータ数と等しくなるようにアンダーサンプリングしたデータを用いてモデルを構築することが多いです。これによって、正例のデータも精度よく分類できるようになりますが、正例と負例のデータ数のバランスがもとのデータと異なるため、確率の予測結果に、アンダーサンプリングによるバイアスが生じてしまいます。
この問題への対処法は、すでに下記のブログなどにまとめている方もいらっしゃいますが、アンダーサンプリングしたデータで構築したモデルが出力する確率のバイアスを除去し、補正する方法について、備忘録としてまとめます。本記事では、確率予測のためのモデルとして、シンプルにロジスティック回帰モデルを利用します。
アンダーサンプリングによるバイアスの補正方法
アンダーサンプリングによるバイアスの補正方法は、論文[Calibrating Probability with Undersampling for Unbalanced Classification]
(https://www3.nd.edu/~dial/publications/dalpozzolo2015calibrating.pdf)で提案されています。
いま、説明変数 $X$ から目的変数 $Y$($Y$は0か1のいずれかの値をとる)を予測する二値分類タスクを考えます。
もともとのデータセット $(X, Y)$ を、正例のデータ数が極端に少ない不均衡データとし、アンダーサンプリングにより負例のデータ数を正例のデータ数と等しくしたデータセットを $(X_s, Y_s)$ とします。また、$(X, Y)$ に含まれるあるデータ(サンプル)が、$(X_s, Y_s)$ にも含まれる場合に1をとり、$(X_s, Y_s)$ に含まれない場合に0をとるサンプリング変数 $s$ を導入します。
もともとのデータセット $(X, Y)$ を用いて構築したモデルに説明変数を与えたとき、正例と予測する確率は $p(y=1|x)$ と表現されます。また、アンダーサンプリングしたデータセット $(X_s, Y_s)$ を用いて構築したモデルに説明変数を与えたとき、正例と予測する確率は $p(y=1|x,s=1)$ と表現されます。$p=p(y=1|x), p_s=p(y|x,s=1)$ とすると、$p$ と $p_s$ の関係は以下のようになります。
p=\frac{\beta p_s}{\beta p_s-p_s+1}
ここで、$\beta=N^+/N^-$($N^+$ は正例のデータ数、$N^-$ は負例のデータ数)です。
導出
以下は詳細な式の説明なので、興味がない方は読み飛ばしてください。
ベイズの定理、および $p(s|y,x)=p(s|y)$ から、アンダーサンプリングしたデータセット $(X_s, Y_s)$ を用いて構築したモデルが予測する確率は下記のように書けます。
p(y=1|x,s=1)=\frac{p(s=1|y=1)p(y=1|x)}{p(s=1|y=1)p(y=1|x)+p(s=1|y=0)p(y=0|x)}
いま、正例のデータ数が極端に少なく、$y=1$ となるデータはすべてサンプリングされるため、$p(s=1|y=1)=1$ とすると、
p(y=1|x,s=1)=\frac{p(y=1|x)}{p(y=1|x)+p(s=1|y=0)p(y=0|x)}
と書けます。
さらに、$p=p(y=1|x), p_s=p(y|x,s=1), \beta=p(s=1|y=0)$ とすると、
p_s=\frac{p}{p+\beta(1-p)}
となります。最後に、$p$が左辺にくるように変形すると、
p=\frac{\beta p_s}{\beta p_s-p_s+1}
となります。
最後の式が意味することは、アンダーサンプリングしたデータを用いて構築したモデルが予測する確率 $p_s$ を補正することでバイアスを除去し、もともとのデータを用いて構築したモデルが予測する確率 $p$ を計算できるということです。
ここで、$\beta=p(s=1|y=0)$ は、負例のデータがサンプリングされる確率を表します。いま、負例のデータは正例のデータと同じ数だけサンプリングするため、$\beta=N^+/N^-$($N^+$ は正例のデータ数、$N^-$ は負例のデータ数)に近似できます。
コード例
以下では、実際のコード例を示しつつ、予測確率を補正する実験をします。(以下のコードの動作環境は、Python 3.7.3, pandas 0.24.2, scikit-learn 0.20.3 です。)
実験は以下の流れで行います。
- 不均衡データをそのまま用いてモデルを構築し、分類精度を検証する。
- アンダーサンプリングしたデータを用いてモデルを構築し、分類精度は改善するが、確率の予測精度は低いことを検証する。
- アンダーサンプリングによるバイアスを除去する補正をかけることで、確率の予測精度が改善するかを検証する。
ここでは、UCI Machine Learning Repository で公開されている、Adultデータセットを使います。このデータセットは、性別や年齢などのデータから、個人の年収が50,000$以上か否かを分類するためのデータセットです。
まず、利用するデータを読み込みます。ここでは、Adultデータセットの
adult.data, adult.testをCSVファイルとしてローカルに保存し、前者を学習用データ、後者を検証用データとして使います。
import numpy as np
import pandas as pd
# データの読み込み
train_data = pd.read_csv('./adult_data.csv', names=['age', 'workclass', 'fnlwgt', 'education', 'education-num',
'marital-status', 'occupation', 'relationship', 'race', 'sex',
'capital-gain', 'capital-loss', 'hours-per-week', 'native-country', 'obj'])
test_data = pd.read_csv('./adult_test.csv', names=['age', 'workclass', 'fnlwgt', 'education', 'education-num',
'marital-status', 'occupation', 'relationship', 'race', 'sex',
'capital-gain', 'capital-loss', 'hours-per-week', 'native-country', 'obj'],
skiprows=1)
data = pd.concat([train_data, test_data])
# 説明変数X, 目的変数Yの加工
X = pd.get_dummies(data.drop('obj', axis=1))
Y = data['obj'].map(lambda x: 1 if x==' >50K' or x==' >50K.' else 0) # 目的変数は 1 or 0
# 学習用データと検証用データに分割
train_size = len(train_data)
X_train, X_test = X.iloc[:train_size], X.iloc[train_size:]
Y_train, Y_test = Y.iloc[:train_size], Y.iloc[train_size:]
学習データにおける正例の割合を見ると、およそ24%と負例に比べて少なく、不均衡データといえます。
print('positive ratio = {:.2f}%'.format((len(Y_train[Y_train==1])/len(Y_train))*100))
# 出力=> positive ratio = 24.08%
この学習データをそのまま用いてモデルを構築すると、分類精度はAUC=0.57と低く、再現率(Recall)も0.26と低いことがわかります。学習データにおける負例のデータ数が多く、予測結果が負例となる場合が多くなり、再現率(正例のデータを正しく正例と分類できる割合)が低くなっていると考えられます。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, recall_score
# モデル構築
lr = LogisticRegression(random_state=0)
lr.fit(X_train, Y_train)
# 分類精度を検証
prob = lr.predict_proba(X_test)[:, 1] # 目的変数が1である確率を予測
pred = lr.predict(X_test) # 1 or 0 に分類
auc = roc_auc_score(y_true=Y_test, y_score=prob)
print('AUC = {:.2f}'.format(auc))
recall = recall_score(y_true=Y_test, y_pred=pred)
print('recall = {:.2f}'.format(recall))
# 出力=> AUC = 0.57
# 出力=> recall = 0.26
次に、学習データにおける負例のデータ数が正例のデータ数と等しくなるようにアンダーサンプリングを行い、このデータを用いてモデルを構築すると、分類精度はAUC=0.90, recall=0.86 と大きく改善することがわかります。
# アンダーサンプリング
pos_idx = Y_train[Y_train==1].index
neg_idx = Y_train[Y_train==0].sample(n=len(Y_train[Y_train==1]), replace=False, random_state=0).index
idx = np.concatenate([pos_idx, neg_idx])
X_train_sampled = X_train.iloc[idx]
Y_train_sampled = Y_train.iloc[idx]
# モデル構築
lr = LogisticRegression(random_state=0)
lr.fit(X_train_sampled, Y_train_sampled)
# 分類精度を検証
prob = lr.predict_proba(X_test)[:, 1]
pred = lr.predict(X_test)
auc = roc_auc_score(y_true=Y_test, y_score=prob)
print('AUC = {:.2f}'.format(auc))
recall = recall_score(y_true=Y_test, y_pred=pred)
print('recall = {:.2f}'.format(recall))
# 出力=> AUC = 0.90
# 出力=> recall = 0.86
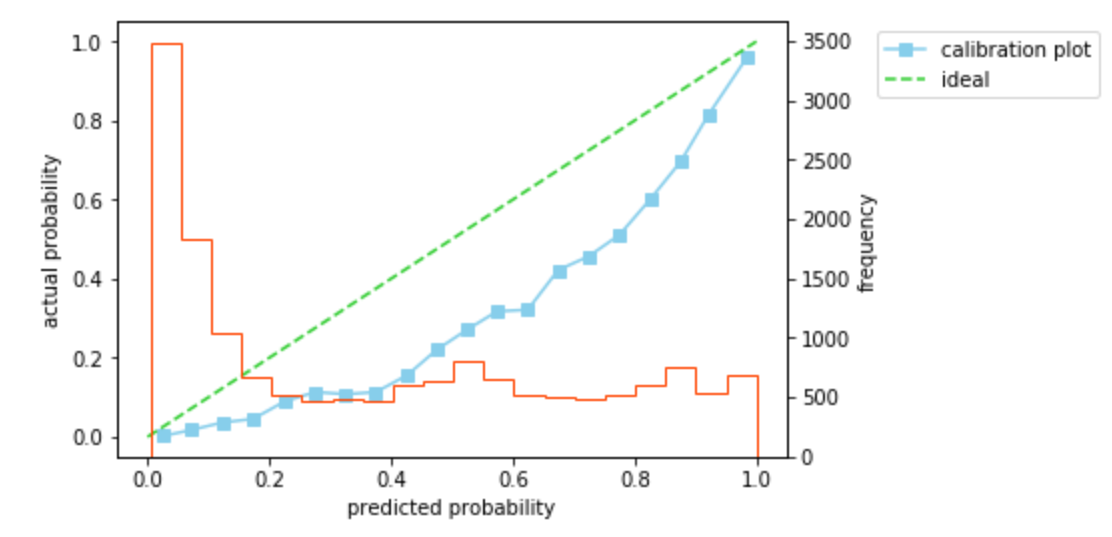
このとき、確率の予測精度を見てみます。ログ損失は0.41、キャリブレーションプロットは45度線よりも下側を通ることがわかります。キャリブレーションプロットが45度線の下側を通ることは、予測した確率が実際の確率よりも大きいことを意味します。いま、負例のデータ数が正例のデータ数と等しくなるようにアンダーサンプリングしたデータを用いてモデルを構築しているため、実際よりも正例のデータ数の割合が大きい状態で学習が行われ、確率が大きめに予測されていると考えられます。
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.calibration import calibration_curve
from sklearn.metrics import log_loss
def calibration_plot(y_true, y_prob):
prob_true, prob_pred = calibration_curve(y_true=y_true, y_prob=y_prob, n_bins=20)
fig, ax1 = plt.subplots()
ax1.plot(prob_pred, prob_true, marker='s', label='calibration plot', color='skyblue') # キャリプレーションプロットを作成
ax1.plot([0, 1], [0, 1], linestyle='--', label='ideal', color='limegreen') # 45度線をプロット
ax1.legend(bbox_to_anchor=(1.12, 1), loc='upper left')
plt.xlabel('predicted probability')
plt.ylabel('actual probability')
ax2 = ax1.twinx() # 2軸を追加
ax2.hist(prob, bins=20, histtype='step', color='orangered') # スコアのヒストグラムも併せてプロット
plt.ylabel('frequency')
plt.show()
prob = lr.predict_proba(X_test)[:, 1]
loss = log_loss(y_true=Y_test, y_pred=prob)
print('log loss = {:.2f}'.format(loss))
calibration_plot(y_true=Y_test, y_prob=prob)
# 出力=> log loss = 0.41
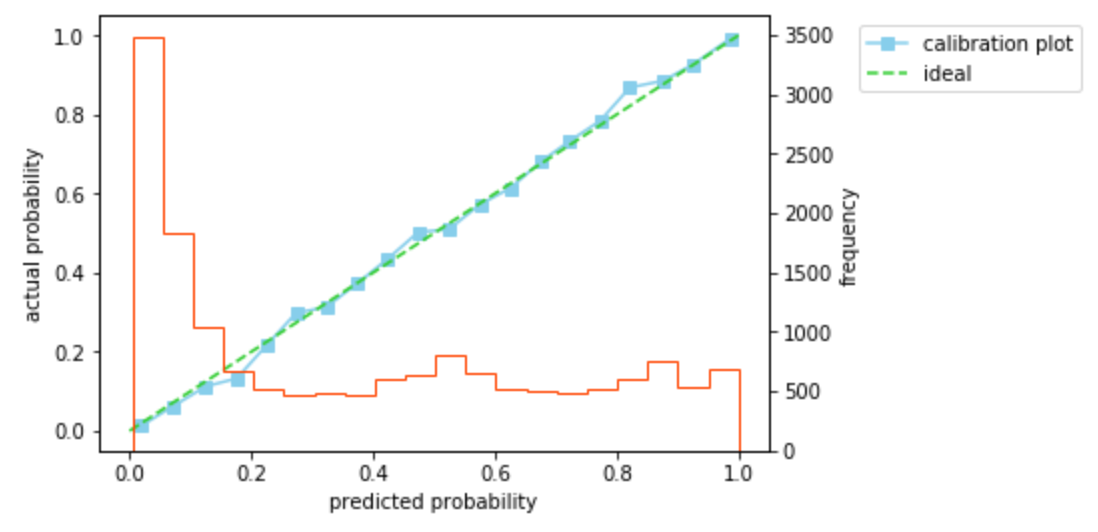
では、アンダーサンプリングによるバイアスを除去し、確率を補正してみます。$\beta$を計算し、$
p=\beta p_s/(\beta p_s-p_s+1$)にしたがって確率を補正すると、ログ損失は0.32と改善し、キャリブレーションプロットもほぼ45度線にのっていることがわかります。ここで、$\beta$は学習用データの正例/負例のデータ数を用いている(検証用データの正例/負例のデータ数は未知としている)ことに注意してください。
beta = len(Y_train[Y_train==1]) / len(Y_train[Y_train==0])
prob_corrected = beta*prob / (beta*prob - prob + 1)
loss = log_loss(y_true=Y_test, y_pred=prob_corrected)
print('log loss = {:.2f}'.format(loss))
calibration_plot(y_true=Y_test, y_prob=prob_corrected)
# 出力=> log loss = 0.32
確かにアンダーサンプリングによるバイアスを除去し、確率を補正できることを確認できました。検証は以上です。
おわりに
この記事では、アンダーサンプリングしたデータを用いて構築したモデルが予測する確率の補正方法について、簡単にまとめました。間違いなどありましたらご指摘いただけますと幸いです。
参考
- 前処理大全 データ分析のためのSQL/R/Python実践テクニック
- [Andrea Dal Pozzolo, et al. "Calibrating Probability with Undersampling for Unbalanced Classification", in Proceedings of IEEE Symposium Series on Computational Intelligence, pp.159-166, Dec. 2015.]
(https://www3.nd.edu/~dial/publications/dalpozzolo2015calibrating.pdf)