はじめに
ベイズ統計モデリングは、データを確率モデル(確率分布とパラメータの関係式)に当てはめ、ある現象がどのように起こったか(=データがどのように生成されたか)を解釈し、将来のふるまいを予測するために用いられる手法です。
勾配ブースティング木やニューラルネットワークなどの機械学習の手法では、ある現象がどのように起こったか、つまり、説明変数と目的変数の関係についての背景知識がなくても、ある程度の予測性能を達成するモデルを構築することができます。しかし、構築したモデルはブラックボックスとなっており、結果の解釈が難しく、どの機械学習の手法が適切なのか(=汎化性能が十分なのか)の判断が難しい場合があります。
一方、ベイズ統計モデリングは、データを使って学習を行う前に、現象に関する背景知識(=データ生成に関する仮定)を確率モデルの形で組み込むことができます。つまり、ドメイン知識・基礎集計などによってデータの性質をあらかじめ把握することで、「データは○○分布に従って生成されている」などの仮説を事前に構築した上で、パラメータなどをデータから学習することができます。これにより、解釈しやすく、かつ予測精度も高いモデルを柔軟に構築することができる利点があります。
この記事では、PyStan / PyMC3 による、ベイズ線形回帰の実装例を備忘録としてまとめます。
ベイズ統計モデリング
ベイズ統計モデリングは、パラメータをすべて確率変数と見做し、データが生成される確率分布を考えます。機械学習の手法では、与えられたデータをもとに学習を行い、各パラメータについて一つの値を求めるのに対し、ベイズ統計モデリングでは、データ $Y$ が与えられたときの各パラメータ $\theta$ の確率分布 $p(\theta | Y)$ を求めることができます。
パラメータの事後確率
データが与えられる前のパラメータの分布 $p(\theta)$ を事前分布(prior distribution)と呼び、データが与えられた後のパラメータの分布 $p(\theta | Y)$ を事後分布(posterior distribution)と呼びます。事前分布と事後分布は、それぞれ事前確率(prior probability)、事後確率(posterior probability)と呼ぶこともあります。事後分布は、ベイズの定理により、以下の式にしたがって求めることができます。
p(\theta | Y) = \frac{p(Y | \theta)p(\theta)}{p(Y)} \propto p(Y | \theta)p(\theta)
これは、事後分布 $p(\theta | Y)$ は、尤度 $p(Y | \theta)$ と事前分布 $p(\theta)$ の積に比例することを表し、$p(Y)$ は正規化定数(事後確率の総和を1にするための定数)と見做せます。尤度 $p(Y | \theta)$ は、パラメータ $\theta$ の値で形状が決まる関数であり、データ $Y$ の当てはまりの良さを表す指標です。一般に、尤度と事前分布の計算は簡単ですが、$p(Y)$ の計算は簡単ではありません。そこで、計算しやすい $p(Y | \theta)p(\theta)$ から乱数サンプルを大量に得ることで事後分布の代わりとする MCMC(Markov Chain Monte Carlo)と呼ばれるサンプリング手法や、計算しやすい式を使って近似的に事後分布を求める変分推論(variational inference)などの手法を用います。
パラメータは確率分布として得られるため、「そのパラメータが取りうる値の範囲(区間)」を求めることができます。特に、事後分布の両端から $\alpha / 2$%を切り取った $(1-\alpha)$%に対応するパラメータの区間を、$(1-\alpha)$%ベイズ信頼区間と呼びます。
予測分布
新しいデータ $y$ に対する予測値についても、一つの値ではなく、確率分布として求めます。この確率分布は、予測分布(predictive distribution)と呼ばれ、以下の式にしたがって求めることができます。
p(y | Y) = \int p(y | \theta)p(\theta | Y)d\theta
これは、データ $Y$ をもとに得られたパラメータの事後分布 $p(\theta | Y)$ で重み付けし、確率分布 $p(y | \theta)$ を足し合わせていることを表します。$p(\theta | Y)$ のサンプル $\theta^+$が MCMC などの手法により得られているとすると、これらのサンプルを用いて、確率分布 $p(y | \theta^+)$ にしたがう乱数 $y^+$ を得ることができます。$y^+$は、予測分布 $p(y | Y)$ からのサンプルと見做すことができ、パラメータの事後分布を求めたときと同様に予測分布を求めることができます。このように求められる予測分布の両端から $\alpha / 2$%を切り取った $(1-\alpha)$%に対応する予測値の区間を、$(1-\alpha)$%ベイズ予測区間と呼びます。
利点
ベイズ統計モデリングには
- ドメイン知識・基礎集計などによってあらかじめ把握できるデータに関する前提知識を、事前分布 $p(\theta)$ として取り込むことができる(ただし、前提知識を確率モデルに落とし込むための数理的な知識が必須)
- パラメータや予測値の確率分布を求めることができるため、予測の不確実性を考慮しつつ、データ分析結果を意思決定に活用できる
という利点があります。
実装例
ここでは、ベイズ統計モデリングの簡単な例として、ベイズ線形回帰を実装します。ベイズ線形回帰の確率モデル式は下記の通りです。
Y_n \sim Normal \biggl (w_0 + \sum_{d=1}^D w_iX_{nd}, ~~ \sigma \biggr) ~~~~~~~~~~ n=1, \dots, N
ここで、$Y_n$ は目的変数、$X_{nd}$ は説明変数、$w_0$ は直線の切片、$w_d ~ (d=1, \dots, D)$ は直線の傾きを表し、$N$ はデータ数、$D$ は説明変数の数を表します。$\sigma$ は、所与の説明変数以外の影響を表現するノイズの大きさです。目的変数と説明変数の関係は、基本的には直線関係 $Y_n = w_0 + \sum_{d=1}^M w_dX_{nd}$ を想定していますが、所与の説明変数以外の影響として、平均0, 標準偏差 $\sigma$ の正規分布から生成されるノイズを加味したモデルとなっています。
ベイズ統計モデリングを行う際は、確率的プログラミング言語を利用する場合が多いです。確率的プログラミング言語は、確率分布の関数や尤度計算に特化した関数を利用できる、統計モデリングに適したプログラミング言語です。本記事では、PyStan / PyMC3 の2つの Python ライブラリを使った実装例を記載します。実行環境は、Python 3.7.6, pystan 2.19.1.1, arviz 0.7.0, pymc3 3.8 です。上記2つのライブラリを使った実装において共通して利用するライブラリ、および利用するデータを生成するコードは以下の通りです。
- 必要なライブラリの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style('whitegrid')
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
- データの生成
ここでは、ベイズ線形回帰の確率モデル通りに生成したデータを利用します。説明変数 X_train, 目的変数 y_train を学習データとし、パラメータの事後分布と検証用データ X_test に対する目的変数の予測分布を算出することを目標とします。
def generate_sample_data(num, seed=0):
target_list = [] # 目的変数のリスト
feature_vector_list = [] # 説明変数(特徴量)のリスト
feature_num = 8 # 特徴量の数
intercept = 0.2 # 切片
weight = [0.2, 0.3, 0.5, -0.4, 0.1, 0.2, 0.5, -0.3] # 各特徴量の重み
np.random.seed(seed=seed)
for i in range(num):
feature_vector = [np.random.rand() for n in range(feature_num)] # 特徴量をランダムに生成
noise = [np.random.normal(0, 0.1) for n in range(feature_num)] # ノイズをランダムに生成
target = sum([intercept+feature_vector[n]*weight[n]+noise[n] for n in range(feature_num)]) # 目的変数を生成
target_list.append(target)
feature_vector_list.append(feature_vector)
df = pd.DataFrame(np.c_[target_list, feature_vector_list],
columns=['target', 'feature0', 'feature1', 'feature2',
'feature3', 'feature4', 'feature5', 'feature6', 'feature7'])
return df
data = generate_sample_data(num=1000, seed=0)
X = data.drop('target', axis=1)
y = data['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
PyStan による実装
PyStan
PyStan は、確率的プログラミング言語の代表格である Stan を Python で利用可能とするインターフェースを提供するライブラリです。確率分布を計算するアルゴリズムとして、MCMC の一種であるハミルトニアンモンテカルロ(HMC: Hamiltonian Monte Carlo)の一実装である NUTS(No-U-Turn Sampler)を利用しています。また、変分推論の一実装である ADVI(Automatic Differentiation Variational Inference)を利用することもできます。
コード例
- 必要なライブラリの読み込み
pystan に加えて、パラメータの事後分布の推定結果を可視化するためのライブラリとして、arviz を利用します。
import pystan
import arviz
- モデル構築・予測分布の算出
sample_code という名前の文字列は、確率分布を表現するための Stan コードです。Stan コードは、主に data, parameters, model の3つのブロックから構成されます。data ブロックは観測されているデータの宣言、parameters ブロックは求めたいパラメータや値が決まっていない確率変数の宣言、model ブロックは尤度や事前分布を記述するために利用されます。また、generated quantities ブロックは、予測分布を求めたい場合など、事後分布とは別に Stan 側で新たにサンプリングしたい変数を定義するために利用されます。
具体的には、下表のように各ブロックを記述しています。
| ブロック | 内容 |
|---|---|
| data | 学習用データ数 N, 説明変数の数 D, 学習用データの説明変数 X, 学習用データの目的変数 y, 検証用データ数 N_new, 検証用データの説明変数 X_new |
| parameters | 切片 w0, 傾き(各説明変数の回帰係数) w, ノイズの大きさ sigma |
| model | ベイズ線形回帰の確率モデル式 |
| generated quantities | 検証用データ X_new に対する目的変数 y_new の計算式 |
data ブロック、parameters ブロック内の <lower=0> は、値の下限を0とするための記述です。model ブロックにおいて、parameters ブロックで宣言したパラメータの事前分布を記述していませんが、デフォルトで無情報事前分布として一様分布が設定されます。また、generated quantities ブロック内の normal_rng() は、正規分布に従う乱数を生成するための関数です。
sample_data は、stan コード(sample_code)における data ブロックと、python 上のデータの対応付けをする辞書です。
sample_code = """
data {
int<lower=0> N;
int<lower=0> D;
matrix[N, D] X;
vector[N] y;
int<lower=0> N_new;
matrix[N_new, D] X_new;
}
parameters {
real w0;
vector[D] w;
real<lower=0> sigma;
}
model {
for (i in 1:N)
y[i] ~ normal(w0 + dot_product(X[i], w), sigma);
}
generated quantities {
vector[N_new] y_new;
for (i in 1:N_new)
y_new[i] = normal_rng(w0 + dot_product(X_new[i], w), sigma);
}
"""
sample_data = {
'N': X_train.shape[0],
'D': X_train.shape[1],
'X': X_train,
'y': y_train,
'N_new': X_test.shape[0],
'X_new': X_test
}
Stan コード(sample_code)をコンパイルします。
sm = pystan.StanModel(model_code=sample_code)
sample_code に記述した確率モデルと、所与のデータ(sample_data)をもとに、パラメータ $w_0, w_1, \dots, w_D, \sigma$ の事後分布を計算し、さらに X_test に対する目的変数の予測分布を計算します。ここでは、sampling()関数を使い、サンプリング結果を fit に格納します。
fit の中身は以下の通りです。
まず、2,3行目はサンプリングの設定を表示しています。2行目に 4 chains, each with iter=1000; warmup=500; thin=1 とありますが、これは chain 数が 4、iteration ステップ数が 1000、warm up ステップ数が 500、thinning ステップ数が 1 であることを表します。サンプリングは、ある初期値を適当に定めて開始し、得られたサンプルをもとに次のステップのサンプルを生成します。これを iteration ステップ数だけ繰り返して得られるサンプルの系列を chain と呼びます。また、サンプリングのはじめのうちは初期値への依存が大きいため、サンプルの系列から除外します。除外するステップ数を warm up(または burn in)と呼びます。さらに、得られるサンプルの自己相関が高く有用なサンプリングが行えていない場合、何ステップかのうち1回だけサンプリングを行うことで状況が改善する場合があります。このようにサンプルを間引くことを thinning と呼びます。実装例では、chain を得る操作を4回行っており、各 chain は 1000ステップだけサンプリングを繰り返し、はじめの500ステップ分のサンプルは除外することで得ています。thinning は行っていません。その結果、3行目にあるように、(1000-500)×4=2000 個のサンプルが得られています。
5行目以降の表は、サンプリングした各パラメータを要約した統計情報です。1列目はパラメータ名、2列目 mean はサンプルの平均値(事後平均(posterior mean)と呼ばれる)、3列目 se_mean は事後平均の標準誤差、4列目 sd はサンプルの標準偏差、5~9列目はサンプルの分位数を表します。10列目 n_eff は、実効的なサンプル数、11列目 Rhat はサンプリングアルゴリズムが収束したかを表す指標です。収束とは、これ以上サンプリングを繰り返しても事後分布の形状が変化しないことを指します。n_eff は自己相関などから判断され、少なくとも100程度あることが望ましいようです。Rhat は Gelman-Rubin 統計量と呼ばれ、「chain 数が3個以上ですべてのパラメータで Rhat<1.1」であれば収束したと見做すようです。実装例では、サンプリングアルゴリズムが収束していることがわかります。
fit = sm.sampling(data=sample_data, iter=1000, chains=4)
print(fit)
# 出力:=>
# Inference for Stan model: anon_model_92cd13fa4b6e158fdf4f4ede934e6196.
# 4 chains, each with iter=1000; warmup=500; thin=1;
# post-warmup draws per chain=500, total post-warmup draws=2000.
#
# mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
# w0 1.6 1.4e-3 0.05 1.51 1.57 1.61 1.64 1.7 1270 1.0
# w[1] 0.19 6.3e-4 0.03 0.12 0.17 0.19 0.21 0.25 2726 1.0
# w[2] 0.35 6.6e-4 0.03 0.28 0.33 0.35 0.37 0.41 2531 1.0
# w[3] 0.5 7.0e-4 0.03 0.43 0.47 0.5 0.52 0.57 2479 1.0
# w[4] -0.41 6.7e-4 0.03 -0.48 -0.44 -0.41 -0.39 -0.35 2633 1.0
# w[5] 0.08 6.3e-4 0.03 0.02 0.06 0.08 0.11 0.15 2795 1.0
# w[6] 0.21 6.9e-4 0.04 0.15 0.19 0.21 0.24 0.28 2605 1.0
# w[7] 0.47 6.5e-4 0.03 0.41 0.45 0.47 0.49 0.53 2449 1.0
# w[8] -0.33 6.8e-4 0.03 -0.39 -0.35 -0.33 -0.3 -0.26 2591 1.0
# sigma 0.28 1.3e-4 7.2e-3 0.26 0.27 0.27 0.28 0.29 2881 1.0
# y_new[1] 2.61 5.8e-3 0.27 2.1 2.42 2.61 2.79 3.13 2136 1.0
# y_new[2] 2.09 6.3e-3 0.28 1.54 1.9 2.1 2.29 2.65 2028 1.0
# y_new[3] 1.72 6.2e-3 0.28 1.2 1.53 1.72 1.91 2.27 2019 1.0
# y_new[4] 2.18 6.5e-3 0.28 1.66 1.99 2.19 2.36 2.77 1894 1.0
# y_new[5] 2.47 6.1e-3 0.28 1.94 2.27 2.47 2.67 3.01 2150 1.0
# (以下省略)
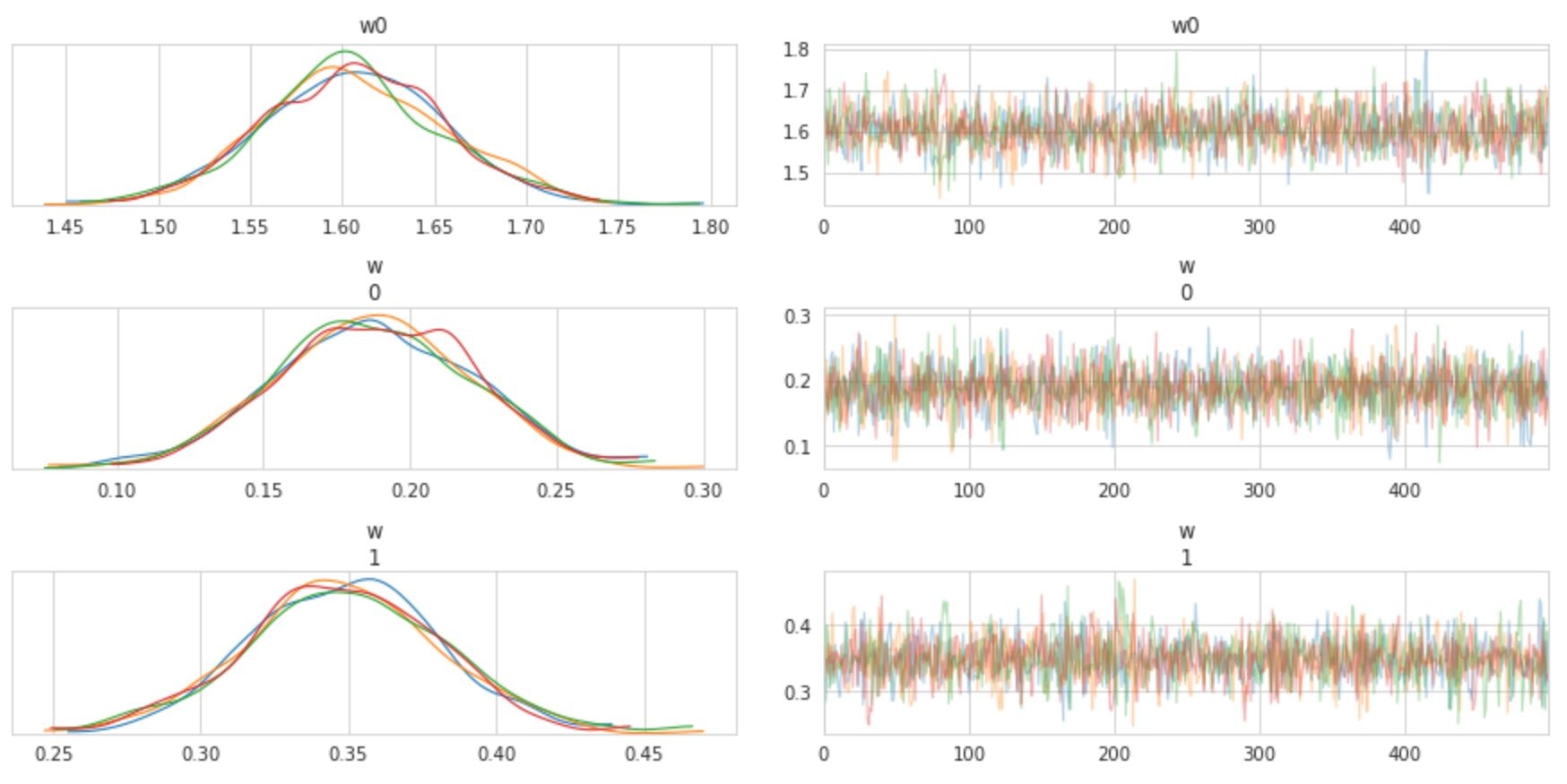
arviz ライブラリの plot_trace()関数を使うと、各パラメータの分布、および trace plot(横軸にステップ数、縦軸にサンプリングした値をプロットした図)を描画することができます。下図は一部のパラメータについて描画したものです。
arviz.plot_trace(fit)
plt.show()
検証用データ X_test に対する目的変数の予測分布も得られているので、サンプリング結果から求めた事後平均を予測値とすれば、機械学習による予測タスクと同様に精度検証することも可能です。
y_pred = fit['y_new'].mean(axis=0)
print('MSE(test) = {:.2f}'.format(mean_squared_error(y_test, y_pred)))
print('R^2(test) = {:.2f}'.format(r2_score(y_test, y_pred)))
# 出力:=>
# MSE(test) = 0.07
# R^2(test) = 0.50
PyMC3 による実装
PyMC3
PyMC3 は、Python の文法の枠内で統計モデリングができるライブラリです。行列操作や微分などの数式処理ができる Theano を内部で利用することで、確率分布の計算の高速化を図っています。Stan と同様に、 NUTS アルゴリズムによるサンプリングや ADVI による変分推論が可能です。
コード例
- 必要なライブラリの読み込み
import pymc3 as pm
import theano
- モデル構築
with pm.Model() ブロック内で、確率モデル式と利用データを記述し、サンプリングを実行します。まず、各パラメータの事前分布を設定し、目的変数の確率モデル式を記述します。実装例では、$w_0, w_1, \dots, w_D$ は $(-\infty, \infty)$ の一様分布 Flat() に、$\sigma$ は $(0, \infty)$ の一様分布 HalfFlat() に設定しています。そして、学習用データの説明変数 X_shared とパラメータを用いて目的変数の確率モデル式を記述し、引数 observed に学習用データの目的変数 y_sahred を指定しています。最後に、sample() 関数でサンプリングを実行しています。実装例では、iteration ステップ数を 1000、warm up ステップ数を 500、chain 数を 4 としています。
学習データを Theano の共有変数としている理由は、検証用データに対する予測分布を計算する際に、モデル(=パラメータの事後分布)を再利用するためです。
X_shared = theano.shared(X_train.values)
y_shared = theano.shared(y_train.values)
with pm.Model() as linear_model:
w0 = pm.Flat('w0')
w = pm.Flat('w', shape=X_shared.get_value().shape[1])
sigma = pm.HalfFlat('sigma')
y_obs = pm.Normal('y_obs', mu=w0+pm.math.dot(X_shared,w), sigma=sigma, observed=y_shared, shape=y_shared.get_value().shape[0])
trace = pm.sample(500, tune=500, cores=4)
各パラメータについて得られたサンプル列は、下記のように取得することができます。chains 引数を指定しない場合、すべての chain におけるサンプル列を取得できます。
trace.get_values('w0', chains=0)
# 出力:=>
# array([1.66414789, 1.69065057, 1.5616519 , 1.61380153, 1.59616214,
# 1.61042565, 1.57903886, 1.61347858, 1.58324086, 1.53493892,
# (以下省略)
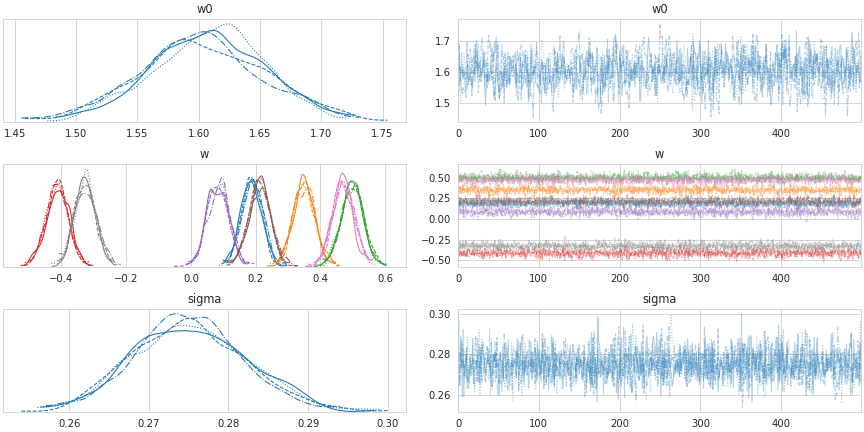
traceplot() 関数により、各パラメータの事後分布と trace plot を描画することができます。
pm.traceplot(trace)
plt.show()
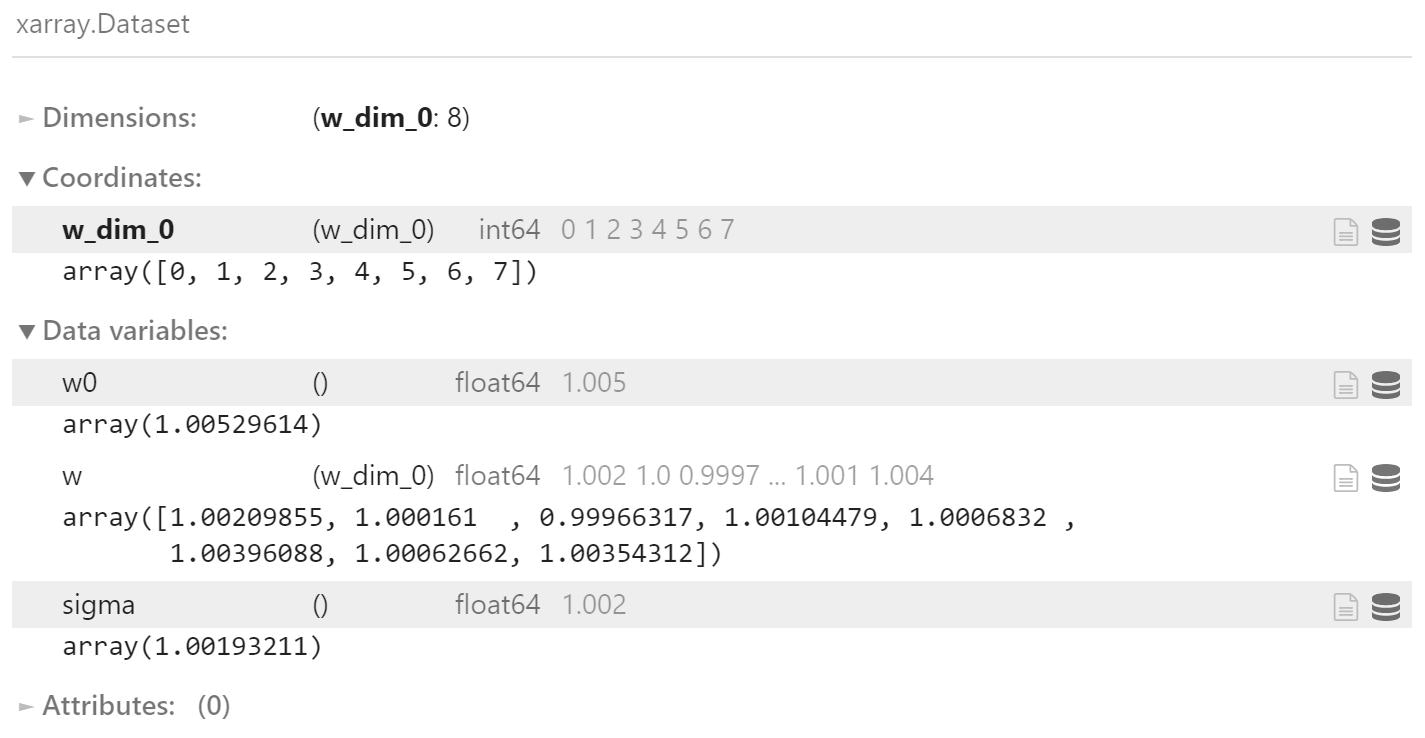
また、gelman_rubin() 関数により、サンプリングアルゴリズムの収束の度合いを表す指標を確認することができます。実装例では、chain 数が 3 以上であり、いずれのパラメータも 1.1 未満となっているため、収束したと見做せます。
pm.gelman_rubin(trace)
さらに、forestplot()関数では、各パラメータについて、各 chain のベイズ信頼区間を表示できます。
pm.forestplot(trace)
plt.show()
- 予測分布の算出
検証用データの説明変数を Theano の共有変数に設定し、確率モデルのブロック内で sample_posterior_predictive() 関数を使用することで、予測分布(=検証用データに対する目的変数のサンプル)が得られます。
X_shared.set_value(X_test)
y_shared.set_value(np.zeros(X_test.shape[0],)) # 目的変数を初期化
with linear_model:
post_pred = pm.sample_posterior_predictive(trace, samples=1000)
サンプリング結果から求めた事後平均を予測値とすれば、機械学習による予測タスクと同様に精度検証することも可能です。(Rstan による実装と同程度の予測精度であることが確認できます。)
y_pred = post_pred['y_obs'].mean(axis=0)
print('MSE(test) = {:.2f}'.format(mean_squared_error(y_test, y_pred)))
print('R^2(test) = {:.2f}'.format(r2_score(y_test, y_pred)))
# 出力:=>
# MSE(test) = 0.07
# R^2(test) = 0.50
おわりに
PyStan / PyMC3 を利用したベイズ統計モデリングの簡単な実装例についてまとめました。
誤りなどありましたら編集リクエストをして頂けると幸いです。