- DeepLearning(1): まずは順伝播(上)
- [DeepLearning(2): まずは順伝播(下)]
(http://qiita.com/eijian/items/24d7e6aee332d59509ec) - DeepLearning(3): そして逆伝播(でも全結合層まで)
- DeepLearning(4): CNNの逆伝播完成?
- DeepLearning(5): スペースリーク解消!
また時間が経ってしまった。畳み込み層の逆伝播のアルゴリズムを理解するのに手間取ってしまった。。。気を取り直して、逆伝播の後半戦といこう。
1. 各層のおさらい
今回作っているプログラムは次のように11層のレイヤで画像を学習・評価している。
| No. | 層 | 実装 |
|---|---|---|
| 0 | 入力 | - |
| 1 | 畳み込み層1 | × |
| 2 | 活性化層1 | ○ |
| 3 | プーリング層1 | × |
| 4 | 畳み込み層2 | × |
| 5 | 活性化層2 | ○ |
| 6 | プーリング層2 | × |
| 7 | 平坦化層 | × |
| 8 | 全結合層1 | ○ |
| 9 | 活性化層3 | ○ |
| 10 | 全結合層2 | ○ |
| 11 | 活性化層4(出力) | ○ |
前回までで全結合層の逆伝播処理は説明したので、それらの処理は実装済み、残るは×のついている層だ(平準化層、プーリング層、畳み込み層)。
その前に、前回のプログラムでは逆伝播において伝播させる誤差($\delta$)を次のようにDoubleの一次元配列(というかリスト)とした。
type Delta = [Double]
しかしプーリング層や畳み込み層では、誤差は単純な一次元配列にならず、画像と同じくXY平面がNチャネルという三次元のデータになる。ということで、次のように改めた。すでに実装済みとした部分もこれに合わせて変更してある。
type Delta = Image -- (= [[[Double]]])
2. 各層の逆伝播処理
2-1. 平坦化(Flatten)層
前回は全結合層までの実装だったので、上記の表で言えば No.11 → No.8 までしかできていなかった。その次の平坦化層(No.7)はCNNの醍醐味である畳み込み層へ誤差を伝えるための重要な転換点だ。が、実装は極めて単純だった。
unflatten :: Int -> Int -> Image -> Image
unflatten x y [[ds]] = split y $ split x ds
where
split :: Int -> [a] -> [[a]]
split _ [] = []
split n ds = d : split n ds'
where
(d, ds') = splitAt n ds
この層の逆伝播処理(unflatten)は、下層から一次元配列で伝わってきた誤差を画像と同じ三次元配列に組み替えて上層に伝えること。画像一枚の画素数(x,y)は引数で与える。第三引数が微妙な形[[ds]]になっているのはDelta型を変更したから。dsの型は[Double]だ。
ちなみに、入力されるデータ数がx,y画素できちんと割り切れることを想定していて何のエラー処理もしていない。。。
2-2. プーリング層
プーリング層にはフィルタ情報がないので、下層から伝播してきた誤差($\delta$)を更新して上層へ伝えれば良い。ただし、プーリング層の更新処理は特殊で、他の層では誤差に何らかの計算処理をすればよいが、プーリング層では次のようなことをしないといけない。
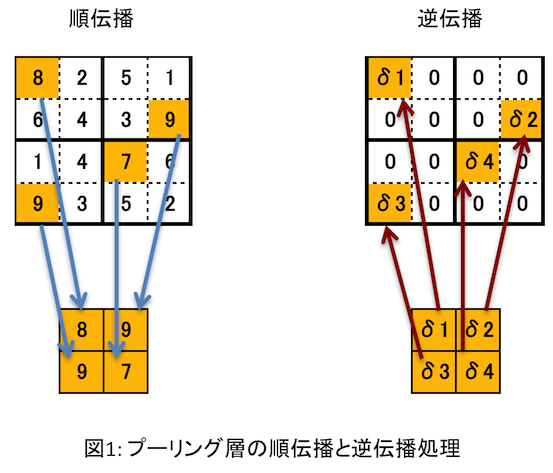
- 順伝播の際に小領域(2x2とか3x3とか)から最大値を選択し、その画素の位置を
覚えておく。 - 逆伝播時は、誤差を順伝播で選択した画素の位置に分配し、小領域のそれ以外の画素には
0を設定する。
これを図にしたらこんな感じ。
前回のプログラムでは、プーリング層への入力画像は記録しているものの、どの画素を選択したかという情報は記録していなかった。yusugomori実装では、選択画素を記録しておく代わりにプーリング層の「出力値=選択された画素」の値を使って、小領域の値と順次比較することでどの画素を選択したかを特定するようになっている。つまり誤差を求めるために「プーリング層の入力値と出力値の両方を使っている」のだ。
しかし私の実装では、逆伝播を再帰で綺麗に(?)処理しようとしたために誤差の計算は「各層の入力値のみ使う」形にしている。このシンプルな構造は維持したい・・・。
結局「プーリング層の入力値を改竄する」ことにした(笑)。そのために順伝播での処理をこう変えた。
- 画像を小領域に分割する(
poolMaxLine) - 小領域の各画素に番号を付ける(
zipで画素値と追番を組(Pix)にする) - 小領域中の画素の最大値を選択する(
max') - 選択した情報を集めると、(最大値,小領域中の追番)の組の集合になる
- 組の第一要素は下層へ伝える出力値、第二要素は「最大値画素の小領域内の
追番(の集合)」になる(poolMax) - プーリング層は引数でもらった入力値をリストから削り、代わりに
「追番の集合」と出力値を返す
プログラムはこうなった。
type Pix = (Double, Double)
:
poolMax :: Int -> Image -> [Image]
poolMax s im = [fst pixs, snd pixs]
where
pixs = unzip $ map unzipPix (poolMax' s im)
:
poolMaxLine :: Int -> [[Double]] -> [Pix]
poolMaxLine _ [] = []
poolMaxLine s ls
| len == 0 = []
| otherwise = pixs : poolMaxLine s ls'
where
len = length $ head ls
pixs = max' $ zip (concatMap (take s) ls) [0.0 ..]
ls' = map (drop s) ls
max' :: [Pix] -> Pix
max' [] = error "empty list!"
max' [x] = x
max' (x:xs) = maximum' x (max' xs)
maximum' :: Pix -> Pix -> Pix
maximum' a@(v1, i1) b@(v2, i2) = if v1 < v2 then b else a
Pixの組の定義で追番がDoubleなのは、追番の集合を「画像」データとして保持するため型を合わせたから。poolMaxで組のリストから「出力値」と「追番集合」を分離して返している。poolMaxLine中の
pixs = max' $ zip (concatMap (take s) ls) [0.0 ..]
が各画素に追番を付けて最大値を選択しているところだ。
forwardLayer :: Layer -> Image -> [Image]
forwardLayer (NopLayer) i = [i]
forwardLayer (ActLayer f) i = [activate f i, i]
forwardLayer (MaxPoolLayer s) i = poolMax s i
forwardLayer (ConvLayer s fs) i = [convolve s fs i, i]
:
forwardLayerにおいてプーリング層だけ他と異なっているのがわかるだろう。他は全て引数のImage(=i)をその層で計算された出力値の後ろにくっつけて返している。プーリング層では"i"をくっつけずPoolMaxの戻り値を使う。これが「入力値を削る」という意味だ。
ここまでが順伝播での「準備段階」。逆伝播の処理は次の通り。
- 誤差と追番を組にする(
depoolMax内のconcatWith) - その組から小領域を生成する(追番のところは誤差値、それ以外は0) (
expand)
順伝播で頑張った分、逆伝播は単純になった。プログラムではこう。
depoolMax :: Int -> Image -> Delta -> (Delta, Layer)
depoolMax s im d = (zipWith (concatWith (expand s 0.0)) im d, MaxPoolLayer s)
where
concatWith :: ([Int] -> [Double] -> [[Double]])
-> [[Double]] -> [[Double]] -> [[Double]]
concatWith f i d = concat (zipWith f (map (map truncate) i) d)
expand :: Int -> Double -> [Int] -> [Double] -> [[Double]]
expand s r ps ds = map concat (transpose $ map split' $ zipWith ex ps ds)
where
split' = split s
ex :: Int -> Double -> [Double]
ex p d = take (s*s) (replicate p r ++ [d] ++ repeat r)
split :: Int -> [a] -> [[a]]
split s [] = []
split s xs
| length xs < s = [xs]
| otherwise = l : split s ls
where
(l, ls) = splitAt s xs
concatWithは少々ややこしいが追番集合を実数から整数に変換して誤差と組にしたうえでexpandに渡している。
これで誤差を上層へ伝播できるわけだ。
2-3. 畳み込み層
(1) 誤差の計算
畳み込み層の逆伝播処理についてわかりやすく説明している書籍やWebサイトを見つけられなかったので理解するのにかなり時間がかかってしまった。唯一yusugomoriさんのblogがあったが、数式が苦手な私には理解は厳しく、結局yusugomori実装のソースを追いかけることになった。。。
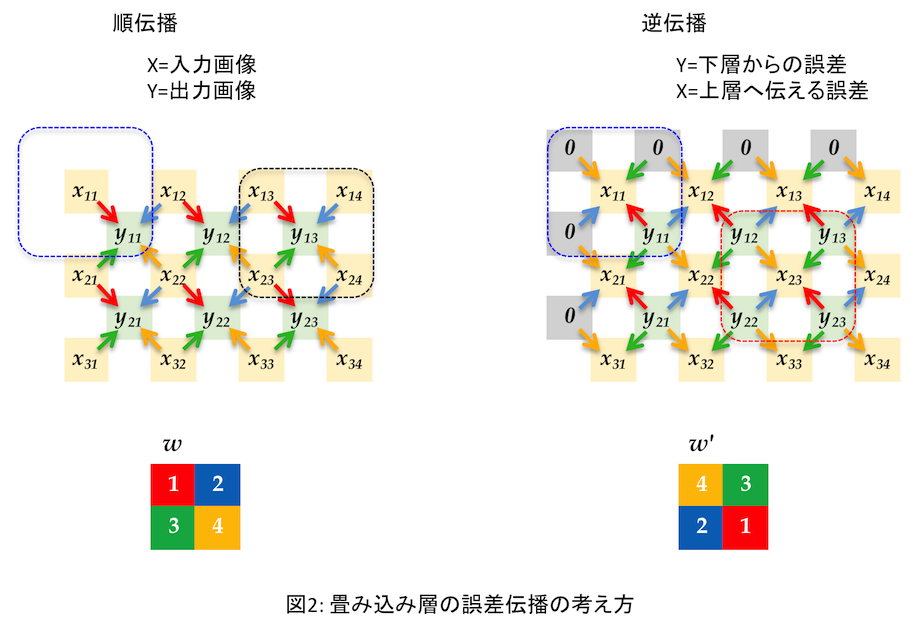
そしてやっと、逆伝播における畳み込み層の誤差計算の仕組みがわかった(つもり)。順伝播と比較するとわかりやすいので図にしてみた。(専門の方には初歩すぎるだろうが、本文章は自身の忘備録を兼ねているため軽く流していただきたい)
この例はフィルタ( $w$ )が2x2の場合である。まず順伝播では、入力画像の4つの画素から出力の画素値を決めている。どの入力画素がどのフィルタ値と掛けられたか矢印を色分けした。たとえば $x_{11}$ は $w$ の1番目(赤、 $w_1$ としよう)を掛けて$y_{11}$ の一部となっているので矢印は赤。 $y_{11}$ を式で書くと、
\displaystyle
y_{11} = x_{11} \cdot w_1 + x_{12} \cdot w_2 + x_{21} \cdot w_3 + x_{22} \cdot w_4
である。一方右の逆伝播の図では、今度は $y_{11}$ が下層から伝播された誤差である。その誤差から上層へ伝える誤差の一つ $x_{11}$ への矢印はやはり赤であるから$w_1$ を掛けるのだ。つまり順伝播と逆をしているだけだ。
しかしプログラム上は $w$ の逆変換(?)である $w'$ (全結合層における $W$ の転置に相当)を求めて使っている。これは「順伝播と同じ畳み込み処理をそのまま使って誤差を求めることができる」からだ(と理解した)。
畳み込み層の順伝播処理では、出力画像の解像度は入力画像のそれより小さくなる。例えばフィルタが2x2で入力が5x5ドットとすると出力は(5-(2-1))x(5-(2-1))=4x4だ。逆伝播では下層から伝播した誤差データの解像度(例えば4x4)が、求めたい誤差データの解像度(たとえば5x5)より小さいのでそのままでは順伝播と同じ処理が使えない。そこで、誤差データに「外枠」を付けて求めたい解像度より大きなサイズにする。右図では上と左に1ドットずつ"0"が並んでいる。これがその「外枠」で、上下左右に同じ幅で追加する必要がある。幅はフィルタサイズで決まる。2x2ならそれぞれ-1して1ドットずつ、3x3ならやはり-1して2ドットずつだ。
ここで、右図の左上の青点線で囲った中を見てみる。各画素から$x_{11}$ が得られているが、 $y_{11}$ 以外は0なので $x_{11} = y_{11} \cdot w'_4 = y_{11} \cdot w_1$ だ。左の順伝播での青点線の中のちょうど逆だ。一方、右図の赤点線の中は $x_{23}$ を周りの $y$ からフィルタ $w'$ を掛けて求めている。これも順伝播での $x_{23}$ の逆なだけ、ただ赤点線の中だけみるとフィルタが順伝播の逆順になっている。これが $w$ の逆変換 $w'$ を使う理由。この $w'$ さえ用意してしまえば、あとは順伝播の処理をそのまま呼び出せばよい。プログラムを見てみよう。
deconvolve :: Int -> [FilterC] -> Image -> Delta -> (Delta, Layer)
deconvolve s fs im d = (delta, ConvLayer s (zip dw db))
where
delta = convolve s fs $ addBorder s d
:
この最後のdeltaが誤差を計算しているところ。fsには予め計算しておいた $w'$ が入っている。下層からの誤差dにaddBorderで「外枠」を付けたら、順伝播のconvolveを呼び出すだけ。ネタがわかってしまえばプログラム自身はとても簡単であった。
(2) 勾配の計算
次に勾配( $\Delta W$ と $\Delta b$ )の計算について考える。まず簡単な方から。 $\Delta b$ は、下層からの誤差を画像の各チャネルで集計するだけ。各チャネルはX,Yの二次元データなのでそれを全て足せば良い。式で書くとしたら下記のような感じか($c$はチャネル番号とする)。
\displaystyle
\Delta b^{(c)} = \sum_{x=1}^N \sum_{y=1}^M \delta_{xy}^{(c)}
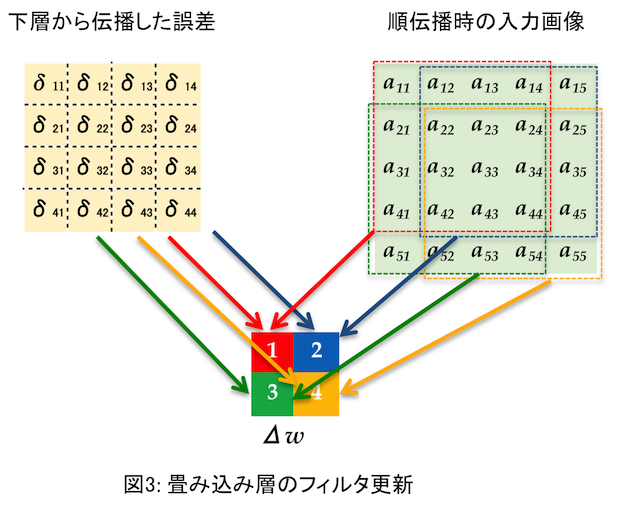
$\Delta W$ の方はちょっとややこしい。下図を見て欲しい。
これは誤差、入力画像とも、とあるチャネルを取り出して $\Delta w$
(一つのフィルタということで小文字)を求める場合だ。それぞれ二次元データになっている。要は $\delta$ と $a$ の該当する画素を掛け合わせて全て足すのだ。ベクトルの内積のような感じ(行列も内積と言うのかな?)。たとえば $\Delta w_1$ (赤)を求めるには、
\displaystyle
\Delta w_1 = \sum_{x=1}^4 \sum_{y=1}^4 \delta_{xy} \cdot a_{xy}
を計算する。それ以外の要素もほぼ同じだが、 $a$ をフィルタの各要素の
場所ぶんだけずらした値を使う。各色の点線で囲った部分を使ってフィルタの
同じ色の要素を計算するわけだ。
これを誤差のチャネル数( $k$ とする)と入力画像のチャネル数( $c$ とする)を
掛けた $k \times c$ 枚計算すれば $\Delta W$ が出来上がる。
プログラムではこうなっている。
deconvolve :: Int -> [FilterC] -> Image -> Delta -> (Delta, Layer)
deconvolve s fs im d = (delta, ConvLayer s (zip dw db))
where
delta = convolve s fs $ addBorder s d
db = map (sum . map sum) d -- delta B
sim = slideImage s im
dw = map (hadamard sim) d -- delta W
slideImage :: Int -> Image -> [[Plain]]
slideImage s im = map (concat . slidePlains s . slidePlain s) im
(slide部分は省略)
hadamard :: [[Plain]] -> Plain -> [[Double]]
hadamard sim ds = map (map (mdot ds)) sim
まずslideImageで上記説明した各色の枠内の $a$ を取り出している。ただし、右や下の使わない部分は、誤差dと突き合わせる際に無視されるためわざわざ切り取っていない(例えば赤点線内は $a_{11}$ から $a_{14}$までだがslideImageで得られるデータには $a_{15}$ も含まれている)。そして、hadamardで誤差dとスライドした入力値を掛け合わせて$\Delta W$ を求めている。
(3) フィルタ更新
(2)までで、ある教師データについて逆伝播の処理内容を説明した。あとはバッチ1回で複数の教師データから得られた各 $\Delta W_i, \Delta b_i$ からフィルタの更新をすればよい。これは全結合の時と同じ式で計算できる。
\displaystyle
\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{1}{N} \sum_{i=1}^{N} \Delta \boldsymbol{W}_i
\displaystyle
\boldsymbol{b} \leftarrow \boldsymbol{b} - \eta \frac{1}{N} \sum_{i=1}^{N} \Delta \boldsymbol{b}_i
この部分はプログラムではこうしている。
updateConvFilter :: Int -> [FilterC] -> Double -> [Layer] -> Layer
updateConvFilter s fs lr dl = ConvLayer s $ zip ks' bs'
where
sc = lr / fromIntegral (length dl)
(ks , bs ) = unzip fs
(kss, bss) = unzip $ map unzip $ strip dl
dbs = vscale sc $ vsum bss
dks = map (mscale sc . msum) $ transpose kss
bs' = vsub bs dbs
ks' = zipWith msub ks dks
strip :: [Layer] -> [[FilterC]]
strip [] = []
strip (ConvLayer s fs:ds) = fs:strip ds
strip (_:ds) = strip ds -- if not ConvLayer
引数fsが更新前のフィルタ($W$や$b$)、dlに各教師データから学習で得られた $\Delta W$ と $\Delta b$ が入っている。これを上式に当てはめて計算するのだ。
さあ、プログラムは完成した!
3. 評価
それでは早速出来上がったプログラムを実行して学習をさせてみよう。(ソースはここ)
$ cabal clean
$ cabal build
:
$ ./dist/build/train/train
Initializing...
Training the model...
iter = 0/200 accuracy = 0.3333333333 time = 0.13968s
iter = 5/200 accuracy = 0.3333526481 time = 11.021087s
iter = 10/200 accuracy = 0.3333741834 time = 21.513648s
iter = 15/200 accuracy = 0.3334006436 time = 33.707092s
iter = 20/200 accuracy = 0.3334352183 time = 45.034608s
iter = 25/200 accuracy = 0.3334818706 time = 55.7984s
:
3-1. 前回分(全結合層のみ)との比較
(1) 学習結果(認識精度)
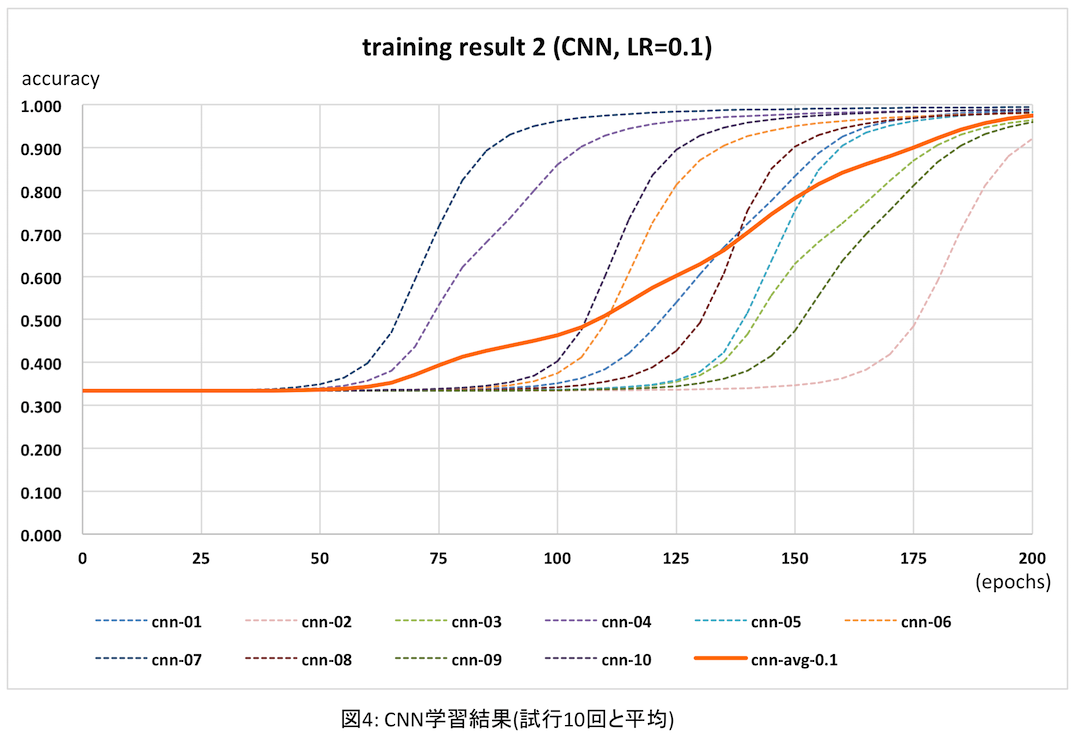
上記のプログラムを10回実行し、それぞれ認識精度と実行時間を計測した。今回epoch数は200(前回は500)としたが理由は後述する。結果は次のグラフのとおり。
点線が各試行時の実測値、太いオレンジの実線が10回の平均だ。各試行では認識精度が向上する時期(epoch)に大変ばらつきがある。これは全結合層の学習でも同じだったが、最初にランダムに設定するフィルタ初期値が良くないからだと思われる。このように向上する時期がバラバラなので、平均を取るとなんだか緩やかに学習が進むように見えてしまう。。。
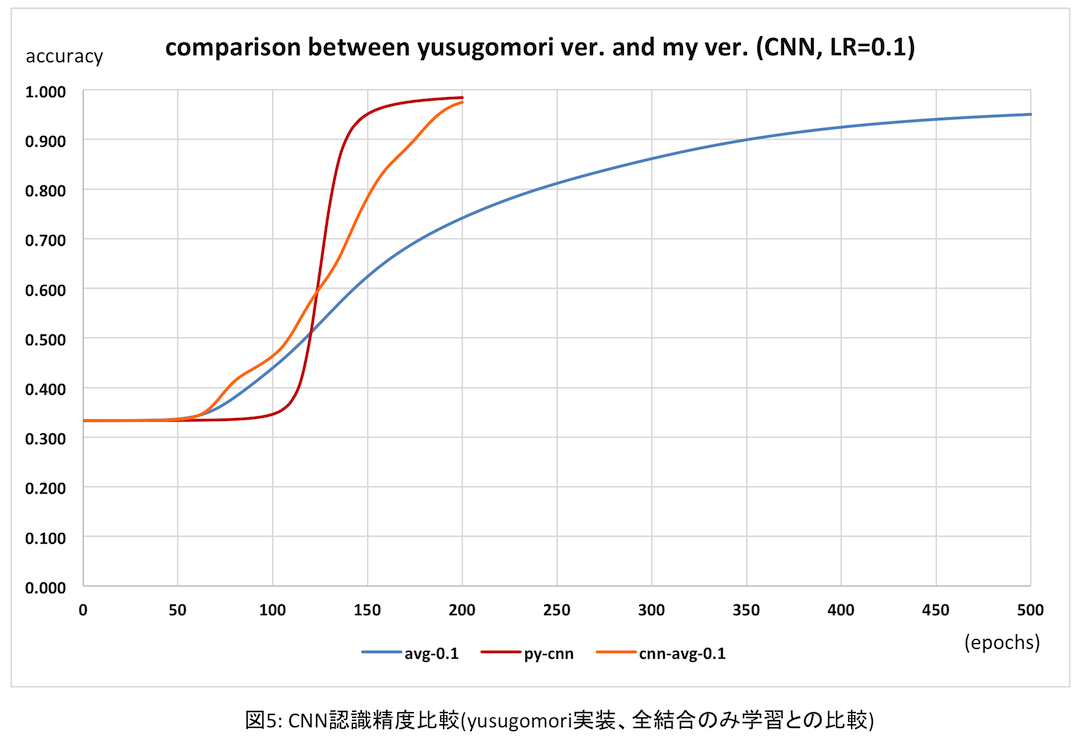
次にyusugomori実装と比較してみる。上記の平均がオレンジ、usugomori実装は赤だ。参考までに前回の全結合のみの場合の平均(青)も比較のため入れた。
オレンジは上述の通り平均値のためなんだかふらついて変だが、最終的にはほぼ同程度の認識精度が得られている。前のグラフを見れば、認識精度の向上具合はyusugomori実装と比べても遜色ないと思われる。(実は逆伝播処理の「値の正しさ」はきちんと検証していないのだが、この結果をみるとそんなに外していないのかな?ということでよしとする)
(2) 処理時間
ただ、いいことばかりではない。畳み込み層まで逆伝播させたため、学習にかかる時間は逆に増えてしまった。200 epoch実行時の結果を次表に示す。
| CNN | 全結合層のみ学習 | |
|---|---|---|
| 処理時間(s) | 517 | 157 |
| 処理性能(epoch/s) | 0.387 | 1.273 |
| 認識精度(%) 200epochs | 97.5 | 74.2 |
| 認識精度(%) 500epochs | - | 95.1 |
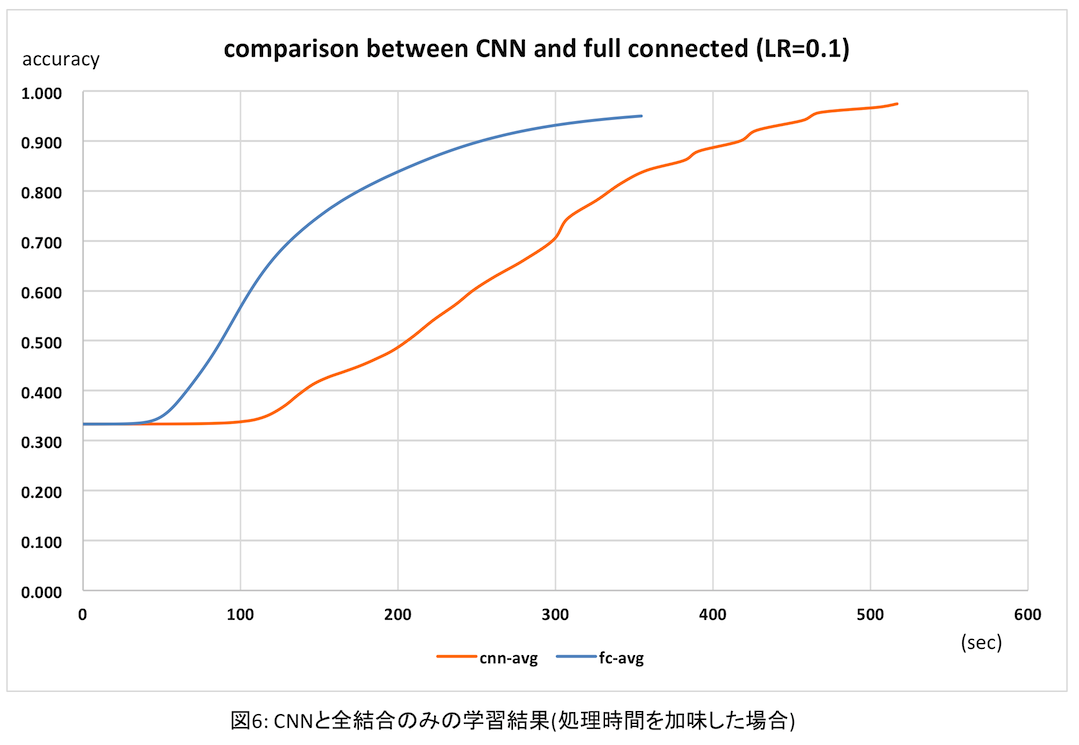
このように、同じ時間で処理できるepoch数が1/3以下に落ちてしまった。さすがに複雑な畳み込み層/プーリング層の逆伝播処理は負荷が高い・・・。同じepoch数ではさすがにCNNの方が認識精度が格段に高い。しかし全結合層のみの学習でも500 epochs続ければ95%を超えるわけで、結局時間と得られる精度はどうなるかと思ってプロットしてみたのが次のグラフ。
このように、処理時間と認識精度を秤にかけると、畳み込み層まで逆伝播させたときは、得られる精度に対しあまりアドバンテージがないように思える。もちろん、認識精度を99%以上まで非常に高くするためには畳み込み層の学習が必要なのだろうと思うが。
一方で、当然ながら私の実装のまずさもあるだろう。やたら再帰を使うとか自分でも頭が混乱するような処理になっているので、もっと簡潔な実装に改められたら改善するかもしれない。今後の課題の一つだ。
3-2. メモリリーク!?
さて、表題に「逆伝播完成?」とクエスチョンを付けた理由がこれだ。epoch数を200に下げた理由も。
やっとできたと思ってepoch数500で実行してみるとなかなか終わらない。開始時は1 epochの処理に約2秒かかったので単純計算では1000秒になるが30分経っても350程度。おかしいと思ってtopコマンドでプロセスを見てみたらメモリを10GBも食っていたのですぐ停止した!
気を取り直してもう一度実行したときのtopコマンドの出力がこれ。trainプロセスが大量のメモリを消費しているのがわかる。これは繰り返し回数がだいたい180ぐらいのときの状態。
Processes: 162 total, 3 running, 159 sleeping, 639 threads 00:22:32
Load Avg: 1.99, 1.98, 1.80 CPU usage: 8.48% user, 32.11% sys, 59.40% idle
SharedLibs: 92M resident, 33M data, 6516K linkedit.
MemRegions: 23895 total, 477M resident, 29M private, 103M shared.
PhysMem: 4080M used (1131M wired), 14M unused.
VM: 471G vsize, 623M framework vsize, 71855224(48041) swapins, 73935000(0) swapo
Networks: packets: 631497/460M in, 456172/62M out.
Disks: 2706786/300G read, 1541857/302G written.
PID COMMAND %CPU TIME #TH #WQ #PORT MEM PURG CMPRS PGRP
25694 train 81.4 08:49.94 1/1 0 10 1064M- 0B 4044M+ 25694
0 kernel_task 76.5 02:28:47 114/7 0 2 443M- 0B 0B 0
:
Macのメモリ管理についてはよく知らないが、trainプロセスの使用メモリが1064M、CMPRSが4044Mで、合わせて5100M=5GBほども消費している。これはいただけない。
本実装ではやたら(無駄に?)再帰を使ってしまっているが、その効率が悪いのかもと思いつつ、消費メモリが増える一方なのはヒープ領域をやたら使っているのだろう。ググると、foldl'を使えとかサンクがどうとかいろいろあるみたいだが、簡単には解決しそうになかったので今回はここまで。対策は次回に頑張ろうと思う。
4. まとめ
今回でやっと一通りCNNが実装できた。学習能力も手本としたyusugomori実装と同等のものができた。しかしながら、上述のとおりメモリを大量に消費するという問題を抱えたままで、このままでは全く実用に耐えない。
次回はこの問題を解決させたいと思う(できないかも・・・)。