- DeepLearning(1): まずは順伝播(上)
- [DeepLearning(2): まずは順伝播(下)]
(http://qiita.com/eijian/items/24d7e6aee332d59509ec) - DeepLearning(3): そして逆伝播(でも全結合層まで)
- DeepLearning(4): CNNの逆伝播完成?
- DeepLearning(5): スペースリーク解消!
第1、2回で順伝播の処理は実現した。今回やっと「学習」処理に入る。(それにしても時間が取れず、またしてもだいぶあいだが空いてしまった。記憶が飛んでいる)
前回作成したプログラムでは、多段のニューラルネットワークを構成したが、その終盤には2つの全結合層(隠れ層と出力層)が含まれている。本稿では、逆伝播による学習で全結合層のフィルタ(ウェイト)を更新する部分について解説し、学習によりフィルタの分類能力が向上することを確認したい。
今回のソースはこちら。
1. 全結合層の逆伝播処理
1-1. 処理の流れ
逆伝播の理論や数式の詳細は各種書籍やWebサイトを見ていただくとして、コード実装の説明に必要な事項をざっと説明しよう。畳み込み層の逆伝播はちょっと複雑っぽいので次回にし、今回は全結合層だけにしておく。
損失関数
「学習」とは、例えば画像認識では入力画像から「犬」や「猫」を正しく判断できるように各層のフィルタを修正してくことだ。(だから本プログラムでは全結合層と畳み込み層がその対象なのだが、今回は全結合層だけ。)
修正するにはまず「どれぐらい正解とずれているか」を確認しないといけない。これを損失関数 $E$ で測る。今回は出力層の活性化関数にsoftmaxを使っており、出力値と正解値の誤差を簡単にするため $E$ には交差エントロピー関数を採用した。
E = -\sum_k t_k \ln y_k \qquad (1)
ここで、$t$ は正解値(ベクトル)、$y$は出力値(ベクトル)だ。例えば本プログラムでは画像を3種類に分類するのでベクトルの要素数は3、仮に教師データを分類1とするなら、
t = [1.0, 0.0, 0.0]\\ y = [0.7, 0.1, 0.2]
といった感じだ。
フィルタの更新
さて損失関数で表される「ずれ」を小さくするため、フィルタ $\boldsymbol{W}$ を更新する。大雑把には次の通り。
\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \Delta \boldsymbol{W} \qquad (2)
ここで、 $\eta$ は学習率(learning rate)と呼ばれるパラメータだ。さて問題は $\Delta \boldsymbol{W}$ をどう求めるかだが、損失関数 $E$ の勾配で表すことができるようだ。
全結合層のフィルタ $\boldsymbol{W}$ は入力数 $\times$ 出力数の行列と見ることができる。その個々の要素を $w_{ij}$ とすると、
w_{ij} \leftarrow w_{ij} - \eta \frac{\partial E}{\partial w_{ij}} \qquad (3)
と書ける(らしい)。だから、最後の偏微分を解けばめでたしめでたしとなる(が、そこが大変)。直接この偏微分を各層で解くと本当に大変だそうだが、実は一つ前の層(出力に近い層)の計算結果をうまく使うとこれが簡単にできる、というのが「誤差逆伝播法」のミソらしい。つまり出力層側から誤差を計算して次の層に渡す。それを元に次の誤差を計算してさらに次の層に渡す。これを繰り返す。
出力層(Lとする)では、上記の偏微分は以下のようになる。
\frac{\partial E}{\partial w_{ij}^{(L)}} = \frac{\partial E}{\partial y_i^{(L)}}
\frac{\partial y_i^{(L)}}{\partial a_i^{(L)}}
\frac{\partial a_i^{(L)}}{\partial w_{ij}^{(L)}}
= \delta_i y_j^{(L-1)} \qquad (4)
\left( \delta_i = \frac{\partial E}{\partial y_i^{(L)}}
\frac{\partial y_i^{(L)}}{\partial a_i^{(L)}} \right)
この $\delta_i$ が次の層へ伝える「誤差」、これに一つ手前の層の結果$y_j$ を掛ける。
順伝播/逆伝播の流れと数式
これらを踏まえ、各層の順伝播・逆伝播を表にしてみた(逆伝播は、今回は全結合層まで)。右上のカッコ付き数字は層の番号。太字はベクトル/行列で、$\boldsymbol{W}_{[3,2]}$ は 3x2行列、のように右下に要素数を記載した。なお、 $\boldsymbol{c}$ は教師データである。(層番号と要素数をつけたら数式が非常に醜くなってしまった。。。)
| No. | 層 | 順伝播 | 逆伝播 | 勾配($\Delta \boldsymbol{W}$) |
|---|---|---|---|---|
| 0 | 入力 | $\boldsymbol{y}_{[12,12,1]}^{(0)}$ | ||
| 1 | 畳み込み層1 | $\boldsymbol{a}_{[10,10,10]}^{(1)}, a_{cij}^{(1)}=\sum_c \sum_s \sum_t w_{st}^{(1)} y_{(s+i)(t+j)}^{(0)}$ | ||
| 2 | 活性化層1 | $\boldsymbol{y}_{[10,10,10]}^{(2)} = \max (\boldsymbol{a}^{(1)}, 0)$ | ||
| 3 | プーリング層1 | (複雑なので割愛) | ||
| 4 | 畳み込み層2 | $\boldsymbol{a}_{[4,4,20]}^{(4)}, a_{cij}^{(4)} = \sum_c \sum_s \sum_t w_{st}^{(4)} y_{(s+i)(t+j)}^{(3)}$ | ||
| 5 | 活性化層2 | $\boldsymbol{y}_{[4,4,20]}^{(5)} = \max (\boldsymbol{a}^{(4)}, 0)$ | ||
| 6 | プーリング層2 | (複雑なので割愛) | ||
| 7 | 平坦化層 | $\boldsymbol{y}_{[80]}^{(7)} \leftarrow \boldsymbol{y}^{(6)}$ | $\boldsymbol{\delta}_{[80]}^{(7)} = {}^t\boldsymbol{W}_{[20,80]}^{(8)} \cdot \boldsymbol{\delta}^{(8)}$ | |
| 8 | 全結合層1 | $\boldsymbol{a}_{[20]}^{(8)} = \boldsymbol{W}_{[80,20]}^{(8)} \cdot \boldsymbol{y}^{(7)} + \boldsymbol{b}_{[20]}^{(8)}$ | $\boldsymbol{\delta}_{[20]}^{(8)} = f'(\boldsymbol{a}^{(8)}) \odot \boldsymbol{\delta}^{(9)}, ; {\scriptsize where : f = \max}$ | $\Delta w_{kl}^{(8)} = \delta_k^{(8)} \cdot y_l^{(7)},\; b_k^{(8)} = \delta_k^{(8)}$ |
| 9 | 活性化層3 | $\boldsymbol{y}_{[20]}^{(9)} = \max (\boldsymbol{a}^{(8)}, 0)$ | $\boldsymbol{\delta}_{[20]}^{(9)} = {}^t\boldsymbol{W}_{[3,20]}^{(10)} \cdot \boldsymbol{\delta}^{(10)}$ | |
| 10 | 全結合層2 | $\boldsymbol{a}_{[3]}^{(10)} = \boldsymbol{W}_{[20,3]}^{(10)} \cdot \boldsymbol{y}^{(9)} + \boldsymbol{b}_{[3]}^{(10)}$ | $\boldsymbol{\delta}_{[3]}^{(10)} = \boldsymbol{y}^{(11)} - \boldsymbol{c}$ | $\Delta w_{ij}^{(10)} = \delta_i^{(10)} \cdot y_j^{(9)},; b_i^{(10)} = \delta_i^{(10)}$ |
| 11 | 活性化層4(出力) | $\boldsymbol{y}_{[3]}^{(11)} = \mathrm{softmax} (\boldsymbol{a}^{(10)})$ |
※ なぜNo.10の逆伝播で $\boldsymbol{\delta} = \boldsymbol{y} - \boldsymbol{c}$ となるのかはそっち系のサイト(こことか)や書籍を読んでほしい。
誤差 $\delta$ が各層で計算され、次の層へ伝わっていくイメージが伝わるだろうか?これをすべての層に対して遡っていけば、めでたく一個の教師データに対する学習が完了するわけだ。
実際には複数個(N)の教師データについて $\Delta \boldsymbol{W}$ を求め、それを平均して $\boldsymbol{W}$ の更新に使う。数式(2)は実際は次のような感じになる。$\boldsymbol{W}$ の右下の $i$ はi番目の教師データから得られたものという意味。
\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{1}{N} \sum_{i=1}^{N} \Delta \boldsymbol{W}_i \qquad (5)
1-2. 誤差逆伝播の実装
面倒な理論・数式の説明はこれぐらいにして、どう実装したか説明しよう。
処理の全体像
下記のmain関数内で呼ばれているtrainLoopが中心部だ。
main = do
:
layers' <- trainLoop getTeachers sampleE putF (learnR st) (layers st) is
:
学習を繰り返すためにepoch番号を入れた配列isを渡していて、学習済みの状態(層リスト)を次に引き渡すためちょっと面倒だが再帰になっている。
trainLoop :: (Int -> IO [Trainer]) -> [Trainer]
-> (Int -> [Layer] -> [Trainer] -> IO ()) -> Double -> [Layer] -> [Int]
-> IO [Layer]
trainLoop _ _ _ _ ls [] = return ls
trainLoop getT se putF lr ls (i:is) = do
ls' <- trainLoop getT se putF lr ls is
teachers <- getT i
let
rls = tail $ map reverseLayer $ reverse ls' -- fist element isn't used
dls = map (train ls' rls) teachers
ls'' = update lr (transpose dls) ls' -- dls = diff of layers
putF i ls'' se
return ls''
trainLoop関数の最初の行でisを一つ減らしてtrainLoopを呼んでいるところ。このため、isの要素がなくなるところまでtrainLoopの呼び出しが続き、最後に「学習前の層リスト」が返され、以後少しずつ層リストを学習で修正する。最後に、学習が完了した層リストがmain中のlayers'に入るという寸法だ。
trainLoopの中では、上記の通り一つ前のepoch番号の学習結果を得てから今回のepochで使う教師データを生成している。yusugomori実装では教師データ数が150個に対しバッチ数が150のため毎回全件で学習しているのだ。
次のrlsはちょっとややこしい。学習では誤差逆伝播法を使うが、そのため層リストを逆順に辿りたい。ただ単純な順序の反転ではダメなので、まず層リストを反転した上で各層を「逆変換」している(reverseLayer)。全結合層ではフィルタ行列の転置が逆変換に相当する。
次の行に出てくるtrainがメイン処理だ。これは後述する。この行で教師データ全部に対し勾配($\Delta \boldsymbol{W}_i$)を計算し、次の行で層リストを更新して終わりだ。なおputFは学習結果を使ってテストデータの認識精度を計算し、表示する処理だ。5 epoch毎に結果を出力する。
次にtrainについて。
train :: [Layer] -> [Layer] -> Trainer -> [Layer]
train [] _ (i, c) = []
train ls rls (i, c) = dls
where
(y, op') = splitAt 1 $ forwardProp ls [i]
d = (head $ head $ head y) `vsub` c
(_, dls) = backwardProp (zip (tail op') rls) (d, [])
where句の次の行は前回までに作成した順伝播処理だ。得られた結果リスト(各層の処理結果)を最後の出力=yとそれ以外に分離している。次の行、yがImage型のため余計な次元を除去して一次元ベクトルにした後で $\boldsymbol{y} - \boldsymbol{c}$ を計算している(にしても3個もheadがあるのは格好悪い)。これが最初の誤差 $\boldsymbol{\delta}^{(10)}$ だ。
3行目が逆伝播の本体。一つ目の引数zip (tail op') rlsは各層の出力値と逆変換用の各層を層毎に組みにしたもののリストだ。逆伝播はこのリストに対して繰り返す。二つ目の引数で前層で計算した誤差と各層の勾配、それを更新して次へ渡す。
backwardProp :: [(Image, Layer)] -> (Delta, [Layer]) -> (Delta, [Layer])
backwardProp [] (_, ls) = ([], ls)
backwardProp ((im,l):ols) (d, ls) = backwardProp ols (d', l':ls)
where
(d', l') = backwardLayer l im d
ここまでが、先述の表と図で説明したものを処理している部分である。うーん、今回も話が長くなりそうだ。
誤差と勾配の計算
逆伝播処理は層の種類で異なるため、backwardLayer関数のパターンマッチで仕分けている。今のところ活性化層(ActLayer)と全結合層(FullConnLayer)のみ実装している。他は次回になんとかしようと思う。
backwardLayer :: Layer -> Image -> Delta -> (Delta, Layer)
backwardLayer (NopLayer) _ d = (d, NopLayer)
backwardLayer (ActLayer f) im d = deactivate f im d
backwardLayer (MaxPoolLayer s) im d = depoolMax s im d
backwardLayer (ConvLayer s fs) im d = deconvolve s fs im d
backwardLayer (FullConnLayer fs) im d = deconnect fs im d
backwardLayer l@(FlattenLayer x y) im d = (head $ head $ unflatten x y [[d]], l)
中身を示そう。まず簡単な活性化層の方から。
deactivate :: ActFunc -> Image -> Delta -> (Delta, Layer)
deactivate f im delta
| c == [0.0] = (zipWith (*) delta f', ActLayer relu')
| c == [1.0] = ([], ActLayer f)
| otherwise = ([], ActLayer f)
where
c = f [0.0]
f' = relu' (head $ head im)
出力に近い方、全結合層の後の活性化層のうち最後の層=出力層ではsoftmax関数を使っているが、誤差を計算する必要がないのでほったらかしている。一方その二つ前の活性化層3(No.9)はReLUを採用しているので、逆関数 $f'$ はステップ関数(relu'として別に定義)になり、前層からきた誤差と掛け合わせている(zipWith (*) delta f'の部分)。
ところで、活性化関数の種類によって処理を変えたいのだが、普通の引数の型(DoubleとかStringとか)や値でのパターンマッチが使えないみたいだ。引数fの値(reluとかsoftmaxとか)で分けられたら楽なんだが。。。それができないので、関数fにダミー値([0.0])を与えた結果で場合分けしている。reluなら0.0に、softmaxなら1.0になるからだ(たぶん)。
次は全結合層の説明。
deconnect :: [FilterF] -> Image -> Delta -> (Delta, Layer)
deconnect fs im delta = (mmul delta fs', FullConnLayer $ calcDiff delta im')
where
fs' = tail fs
im' = head $ head im
calcDiff :: Delta -> [Double] -> [FilterF]
calcDiff delta im = map (mulImage im') delta
where
im' = 1.0:im
mulImage :: [Double] -> Double -> [Double]
mulImage im d = map (*d) im'
誤差は、フィルタfsと前層からの誤差deltaを掛けている(mmul delta fs')。fsはすでに転置行列にしてあるが、その最初の要素はバイアスbに相当するため削る(tail fs)。全結合層は学習によりフィルタを更新するから、誤差から学習に必要な勾配 $\Delta W$を計算している。calcDiffがそれ。誤差値deltaと順伝播での入力値imのそれぞれの要素を掛け合わせて作り出している。本実装ではバイアスbはフィルタに統合されているので、入力値に1.0を加えているが(im' = 1.0:im)。
全結合層のフィルタ更新
さあ最後に、各教師データから得られた勾配を平均してフィルタを更新する部分を見てみよう。
update :: Double -> [[Layer]] -> [Layer] -> [Layer]
update lr _ [] = []
update lr [] ls = ls
update lr (dl:dls) (l:ls) = (updateLayer lr l dl):(update lr dls ls)
dlは処理対象の層lに対する各教師データからの勾配が入っている。これをupdateLayerに渡して計算している。lrは学習率だ。
次が、全結合層での勾配を集計する処理である。
updateFullConnFilter :: [FilterF] -> Double -> [Layer] -> Layer
updateFullConnFilter fs lr dl = FullConnLayer fs'
where
ms = strip dl
delta = mscale (lr / (fromIntegral $ length ms)) $ msum ms
fs' = msub fs delta
ほぼ数式(5)そのままなので、ほぼ説明不要だろう。ms = strip dlについてだけ。各教師データから得た勾配のリストから、この層での対象外のデータがあれば除外するようにしている。普通は問題ないはずだが。
2. 「学習」の評価
プログラムも出来上がったことだし、どれだけ学習するか評価してみよう。コンパイルと実行は次の通り。
% cabal build
:
% ./dist/build/train/train
Initializing...
Training the model...
iter = 0/500 accuracy = 0.3333333333 time = 0.149965s
iter = 5/500 accuracy = 0.3333413554 time = 5.132365s
:
途中経過を 5 epoch 毎に画面に出している。前回から少しフォーマットを変更し、正答率を「認識精度=accuracy」に改めている。
2-1. 学習結果(ノーマル版)
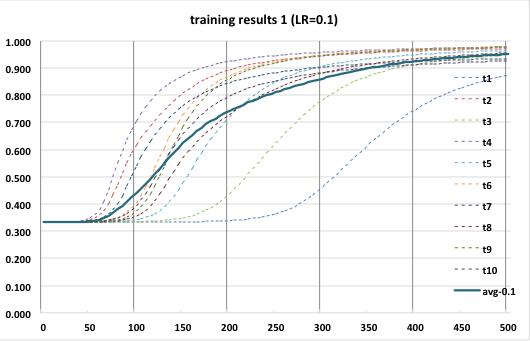
上記のプログラムを10回実行し、それぞれ認識精度と実行時間を計測した。結果は次のグラフの通り。
点線が各試行時の実測値、太い実線が10回の平均値だ。これを見ると、認識精度は各試行でかなりばらついているのがわかる。また、認識精度の向上が急峻なものと緩慢なものがあり、かなり差がある。
プログラムでは、学習用データ、テスト用データ、および各フィルタに乱数を使っているが、それらの初期状態によりこれだけの差が生じてしまっていると思われる。(学習効果が薄い=うまく特徴が出ない画像群が生成されたとか、フィルタの初期状態がイケてないとか)
ただ、総じて 500 epoch ぐらい繰り返せば認識精度がほぼ9割を超えることも分かった。まだ畳み込み層の学習をしていない段階でここまで精度が上がるとは思っておらず、嬉しい誤算だった。(こんなものなのかな?)
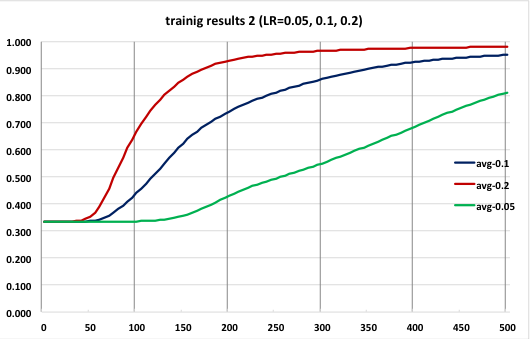
2-2. 学習結果(学習率の差)
先のグラフで、認識精度の向上は最初からではなく50 epochを超えたあたりから急に上がりだしている。私は素人なのでよくわからないが、いろいろな情報を見ると「学習率」はどう設定するかとか、学習進行に応じて変化させるとか書かれていて、重要なパラメータであるらしい。
このプログラムでは学習率を0.1に固定しているが、初期段階ではこれが小さすぎるのかもしれない。ということで、学習率を0.2と0.05に変えて試行した結果も出してみた。(0.2と0.05の試行は5回、その平均をとった)
予想通りかというとちょっと微妙だが、学習率を大きくした方がより速く認識精度が向上していることがわかる。ただ、初っ端から急上昇しているわけではないのでもっと大きくしないといけないのだろう。ただ、大きいままで学習を続けると収束しないという話もある(?)ので、やはり動的に変化させるのがいいのだろう。あとでそれにも取り組みたい。
今回のプログラムはyusugomori実装を「写経」することが第一課題なので学習率は0.1に戻しておこう。
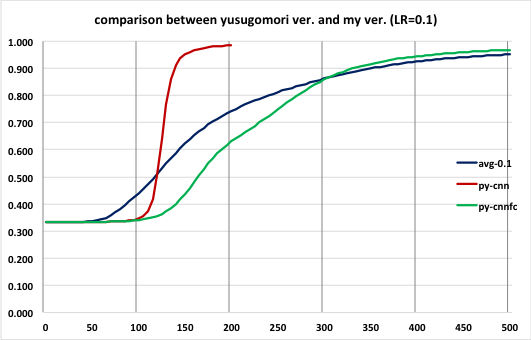
2-3. yusugomori実装との比較
ここまで、学習が進んだ!と喜んできたわけだが、「写経」元のyusugomori実装と同じことができているのだろうか?
ということでyusugomori実装との比較をしてみたのが次のグラフだ。
avg-0.1が本プログラム(学習率0.1、試行10回の平均値、青線)、py-cnnがyusugomori実装(学習率0.1、試行1回、赤線)、py-cnnfcがyusugomori実装で畳み込み層の学習を抑制した改造版(学習率0.1、試行1回、緑線)だ。yusugomori実装では乱数のseedが固定されているため毎回同じ結果になるのと、後で述べるようにめちゃくちゃ処理時間が掛かるのとで試行は1回だけにした。
先述の通り乱数の生成値により試行結果はかなりぶれるのだが、青と緑の線は350 epoch近辺からほとんど同じような値になっていて、(楽観的に見れば)本プログラムはyusugomori実装と同等な処理ができているのではないかと思う。一方本来の学習(=畳み込み層も学習)であれば認識精度が急上昇し、かつ200 epoch ぐらいでも認識精度が98%を超えてくる。それに比べ本プログラムでは畳み込み層のフィルタがいつまでたっても初期状態(ランダム)のままなので、この差は致し方ないところだろう。まあ、ここまで性能差があると早く畳み込み層の学習部分も完成させたいと思うからモチベーションの向上になる。
次に処理時間について見てみる。200 epoch 実行時の結果は次表のとおりである。(iMac early 2009, 3.0GHz Core 2 Duo, 4GB memory)
| avg-0.1 | py-cnn | py-cnnfc | |
|---|---|---|---|
| 処理時間(s) | 157 | 24838 | 6152 |
| 処理性能(epoch/s) | 1.273 | 0.008 | 0.033 |
| 認識精度(%) | 74.2 | 98.4 | 62.9 |
yusugomori実装の処理時間が半端ではないことがわかる。本プログラムもコンパイルされたネイティブコードであることを考えると決して十分な処理速度ではないが、それでもまったく比べものになっていない。
NumPyライブラリのインストールに何か抜けている手順があるのだろうか?インストール時に何か特別なことをした記憶もないので、以下の記事にあるように「ちゃんとした」インストールができていないのかもしれない。
(参考1) Kesin's diary: NumPy, SciPyをちゃんとインストールする
もしくは次の記事のように多重ループと配列要素への直接読み書きが影響しているのかもしれない。
(参考2) numpyで明示的にループを書くと極端に遅くなる
いずれにせよ、当方は今の所Pythonを使う気はないので深入りはしない...
3. まとめ
今回は全結合層部分の逆伝播処理を実装した。これにより学習ができるようになったので、精度はともかく画像認識ができるようになった。ただ、これはまだ半分。次回は畳み込み層の逆伝播を実装し、プログラムを完成させようと思う。