- DeepLearning(1): まずは順伝播(上)
- [DeepLearning(2): まずは順伝播(下)]
(http://qiita.com/eijian/items/24d7e6aee332d59509ec) - DeepLearning(3): そして逆伝播(でも全結合層まで)
- DeepLearning(4): CNNの逆伝播完成?
- DeepLearning(5): スペースリーク解消!
前回に続き、CNNの順伝播処理について。前回は下準備という感じだったが、今回は各層の処理を考よう。
なお今回の記事に限らないが、私の記事は自分自身の忘備録であることが主目的なため、各種技術・理論については正しくないかもしれないしプログラミングに必要なことに絞って書いている。よってCNNやDeep Learningの正しいところは前回紹介したような、各種書籍・Webサイトにあたってほしい。
CNNの組み立て
まずはyusugomoriさんのPython実装(yusugomori実装)を写経するので、そこで定義されているCNNを作りたいと思う。
CNNの構造
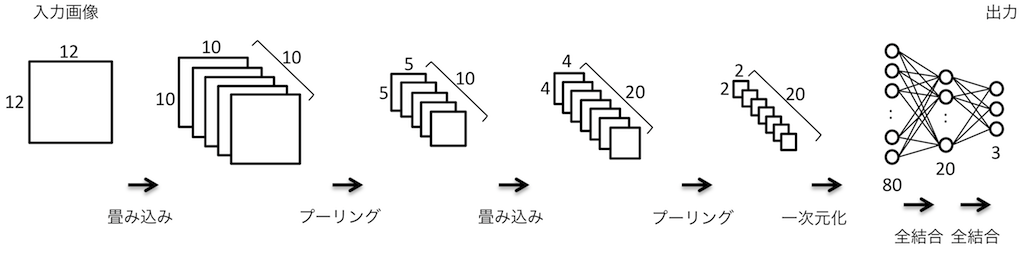
前回出した図をもう一度使うが、作成するCNNの構造は次のようになっている。
- 第1畳み込み層
- 入力画像はモノクロ12x12ドット(1チャネル)
- 畳み込みフィルタは3x3ドット、10枚
- 畳み込みにより10x10ドット、10チャネルの「画像」に変換される
- 第1活性化層
- 活性化関数はランプ関数(ReLU)、全ドットにReLUを適用
- 画像サイズ、チャネル数に変化なし
- 第1プーリング層
- プーリングサイズは2x2ドット
- 最大プーリングを適用
- 出力画像の大きさは10÷2で5x5ドット、10チャネルとなる
- 第2畳み込み層
- 入力画像はモノクロ10x10ドット(10チャネル)
- 畳み込みフィルタは2x2ドット、20枚
- 畳み込みにより4x4ドット、20チャネルの「画像」に変換される
- 第2活性化層
- 活性化関数はReLU、全ドットにReLUを適用
- 画像サイズ、チャネル数に変化なし
- 第2プーリング層
- プーリングサイズは2x2ドット
- 最大プーリングを適用
- 出力画像の大きさは4÷2で2x2ドット、20チャネルとなる
- 一次元化
- 2x2ドット、20チャネルを一次元化して2x2x20=80個のリストに変換
- 隠れ層(全結合層)
- 入力要素は80個、出力要素は20個
- 第3活性化層
- 全要素にReLUを適用
- 出力層(全結合層)
- 入力要素は20個、出力要素は3個
- 第4活性化層
- 全要素にSoftmaxを適用
各層は前回説明したようにmain関数内にLayerのリストとして定義している。
トレーニング
各教師データ(画像)に対して上記のCNNを適用するのだが、一枚毎に次のtrain関数で変換している。前回示したloop関数内で呼び出されている。中身は各層の順伝播処理を呼んでいるだけなので簡単だ。
(Trainer.hs)
train :: [Layer] -> Trainer -> IO (Image, [Layer])
train [] (i, c) = return (i, [])
train ls (i, c) = do
let op = forwardProp ls [i]
ls' = backwordProp ls op
return (head op, ls')
forwardPropが順伝播、backwordPropが逆伝播だが、まだ順伝播のみの実装だ。forwardPropは再帰により層を順に適用し、それぞれの順伝播処理を呼び出すようにした。
(Layer.hs)
forwardProp :: [Layer] -> [Image] -> [Image]
forwardProp [] is = is
forwardProp (l:ls) is = forwardProp ls (forward l is)
forward :: Layer -> [Image] -> [Image]
forward _ [] = []
forward NopLayer i = i
forward l@(ActLayer f) im@(i:is) = (activate l i):im
forward l@(MaxPoolLayer s) im@(i:is) = (poolMax l i):im
forward l@(ConvLayer s fs) im@(i:is) = (convolve s fs i):im
forward l@(HiddenLayer fs) im@(i:is) = (connect fs i):im
forward l@(FlattenLayer f) im@(i:is) = (f i):im
各層の処理
何もしない層(NopLayer)
入力をそのまま返すダミーだ。(プログラムの動作を確認するため)
畳み込み層(ConvLayer)
この層はCNNのキモになるので自分の忘備録のために少し丁寧に記述しておく。畳み込み層では、画像の各チャネルについてフィルタを適用する。フィルタの大きさは3×3などの比較的小さいものだ。一般的でないかもしれないが簡便のため正方形とする。
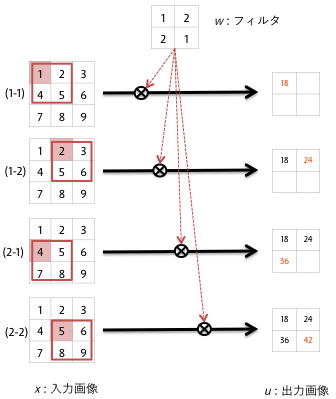
各チャネルの二次元データ上の各画素について、そこを起点にフィルタと同じ大きさの正方形を取り出してフィルタの対応する画素と掛け合わせて合計するのだ。下図では入力を$x$、出力を$u$、フィルタを$w$とする。
$
u_{11}=x_{11}w_{11}+x_{12}w_{12}+x_{21}w_{21}+x_{22}w_{22}
$
$
u_{12}=x_{12}w_{11}+x_{13}w_{12}+x_{22}w_{21}+x_{23}w_{22}
$
$
u_{21}=x_{21}w_{11}+x_{22}w_{12}+x_{31}w_{21}+x_{32}w_{22}
$
$
u_{22}=x_{22}w_{11}+x_{23}w_{12}+x_{32}w_{21}+x_{33}w_{22}
$
この処理、手続き型言語であれば多重ループで難なく書ける処理なのだが、Haskellでどう書くか?画像をリストでなくArrayで表現して、各画素を何度も順序ばらばらにアクセスすればすれば多重ループで書けるが、今回は再帰で処理するために次のようにした。
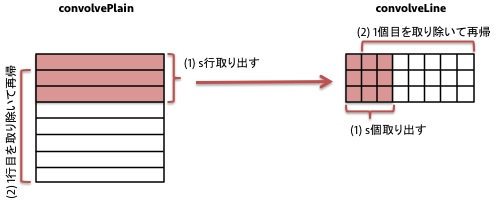
フィルタの大きさをsとすると、画像データの最初のs行をtakeで取り出して各行の処理(convolveLine)を行う。そのあと、1行目を取り除き(tail)、また同じことを繰り返すのだ。残りの行数がフィルタの大きさ(s)より小さくなったら終了する。
(ConvLayer.hs)
-- s: filter size
convolvePlain :: Int -> [Double] -> Plain -> Plain
convolvePlain s k ps
| len < s = []
| otherwise = (convolveLine s k p:convolvePlain s k ps')
where
len = length ps
p = take s ps
ps' = tail ps
各行についてtakeで行の最初からs個取り出すと$s \times s$個の画素データが得られる。これにフィルタを適用する。そのあと、各行の最初の要素を取り除き、それを使って同じ処理を行の要素がs個未満になるまで繰り返す。sum $ zipWith (*)の部分がフィルタを適用しているところである。
(ConvLayer.hs)
convolveLine :: Int -> [Double] -> [[Double]] -> [Double]
convolveLine s k ps
| len < s = []
| otherwise = ((sum $ zipWith (*) vs k):convolveLine s k ps')
where
len = minimum $ map (length) ps
vs = concat $ map (take s) ps
ps' = map (tail) ps
この場合、入力画像のサイズに対し「フィルタのサイズ-1」だけ小さな画像が出力される。今回の例では、元画像が$12 \times 12$、フィルタが$3 \times 3$のため、12-(3-1)=10となり$10 \times 10$の画像が得られる。
もう一つ、フィルタサイズより小さくなった時は黒や白のドットを補うことで入力画像のサイズを維持する手法もあるようだ。が、一般的な画像認識で使われるであろう数百×数百程度の画像では誤差のようなものなので前者の手法を使う。
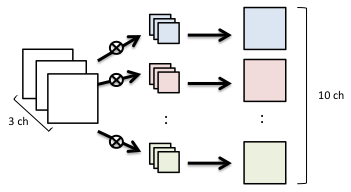
こうすれば、画像の各画素に対して再帰的にフィルタを適用できる。入力画像の1チャネル毎にこの処理を繰り返すと、全体としては下図のように複数チャネルの画像に変換されて出てくるわけだ。
その後、入力画像の各チャネルの処理結果を足し合わせる必要がある。これは各チャネルの同じ位置にある画素データを足すだけなので簡単なことのはずだが、頭がこんがらがって以外と手間取った。
(ConvLayer.hs)
sumPlains :: Double -> [Plain] -> Plain
sumPlains b [] = repeat $ repeat b -- 2 Dimensions (X*Y)
sumPlains b (p:ps) = zipWith f p (sumPlains b ps)
where
f :: [Double] -> [Double] -> [Double]
f [] _ = []
f (a:[]) (b:_) = [a + b]
f (a:as) (b:bs) = (a + b):(f as bs)
特に全チャネル分を足し合わせ、さらにバイアス値を加える必要があるので多少複雑になってしまった。全画素に同じバイアス値を加えるために、repeat $ repeat バイアス値により画像サイズがわからなくても処理できた。普通ならちゃんと画像サイズ分の二次元データを用意するところだろう。細かいところだが、遅延評価の恩恵か。
活性化層/活性化(ActLayer)
先述の通り、ニューラルネットについての書籍やサイトでは活性化層という独立した層として説明されておらず、畳み込み層や隠れ層の後処理的な扱いだ。が、今回は独立した層としたほうが「私にとって」わかり易そうだったので分けることにした。ただ、後でチューニングのために他の層に統合するかもしれない・・・。
活性化関数として、ランプ関数(Rectified Linear Unit, ReLU)とsoftmax関数を用意した。それぞれ下記で表される。これらはActLayer層の作成時にどちらか選ぶのだ。
(ReLU)
$
f(x_i) = \max(x_i, 0)
$
(Softmax)
$
f(\boldsymbol{x}) = \frac{e^{x_i}}{\sum_{k=1}^K e^{x_k}}
$
ここで、$x_i$は$i$番目の出力値、$K$は出力値の個数(次元)である。実装はこう。
(ActLayer.hs)
relu :: ActFunc
relu as = map f as
where
f :: Double -> Double
f a = if a > 0.0 then a else 0.0
softmax :: ActFunc
softmax as = map (\x -> x / sume) es
where
amax = maximum as
es = map (\x -> exp (x - amax)) as
sume = sum es
記事を書いていて、ReLUのほうは素直にmaxを使えばいいと思った。後で直そう。Softmaxの方も、ほぼ定義通りだ。ただし入力xに対し、xの最大値を引いているがこれは発散しないための工夫だそうだ。activate本体はすべての画素に対して活性化関数を適用する。まあ、難しいものではない。
(ActLayer.hs)
activate :: Layer -> Image -> Image
activate (ActLayer f) im = map (map f) im
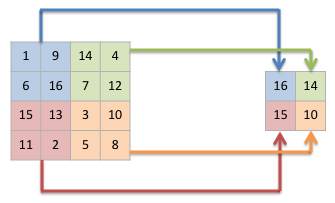
プーリング層(MaxPoolLayer)
本プログラムでは最大プーリングのみ対応する。他も必要になったらその時考えよう。プーリングの処理では画像を小ブロックに分け、その中の各値から出力値を計算する。最大プーリングでは、最大値を選択して出力するわけだ。幾つかの画素から一つだけ値を出力するのだから、当然出力値の数は少なくなる。小ブロックが2x2ドットだとすると、元の画像が縦横半分のサイズになるのだ。
これをプログラムにしてみよう。まず、1チャネルの画像の処理について。
(PoolLayer.hs)
poolMaxPlain :: Int -> Plain -> [[Pix]]
poolMaxPlain s p = map (poolMaxLine s) ls
where
ls = splitPlain s p
splitPlain :: Int -> Plain -> [[[Double]]]
splitPlain s [] = []
splitPlain s p = (p':splitPlain s ps)
where
(p', ps) = splitAt s p
poolMaxPlainが1チャネル分の処理の主体だ。入力データ(Plain)をsplitPlainによってブロックサイズで縦方向に分割している。縦sドットの横に細長いデータをそれぞれpoolMaxLineに引き渡して処理させているのだ。
(PoolLayer.hs)
poolMaxLine :: Int -> [[Double]] -> [Pix]
poolMaxLine _ [] = []
poolMaxLine s ls
| len == 0 = []
| otherwise = (pixs:poolMaxLine s ls')
where
len = length $ head ls
pixs = max' $ zip (concat $ map (take s) ls) [1..]
ls' = map (drop s) ls
max' :: [Pix] -> Pix
max' [] = error "empty list!"
max' [x] = x
max' (x:xs) = maximum' x (max' xs)
maximum' :: Pix -> Pix -> Pix
maximum' a@(v1, i1) b@(v2, i2) = if v1 < v2 then b else a
ここは(今は)余計な処理が入っているためちょっと複雑だ。説明しよう。大まかには、与えられた細長いデータからsドット分を取り出し、max'関数で最大値を選択している。残りのデータは再帰により同じことを繰り返す。ここで処理対象がDoubleではなくPixという型に変わっているが、その定義はこう。
(PoolLayer.hs)
type Pix = (Double, Int)
これは小ブロックの各要素に番号をつけるために用意した型だ。poolMaxLineでは、$s \times s$ドット分取り出したら一次元化してそれに番号を振っている。以下の部分。
zip (concat $ map (take s) ls) [1..]
これは最大プーリングでどの画素が最大だったかを覚えておいて、後々逆伝播処理で伝播先(?)とするために必要だとか(とどこかで読んだはず、だがまだ勉強中で本当かどうかわかっていない。いつのまにかしれっと消えているかもしれない‥)。
二次元データについてpoolMaxPlainで処理できれば、それを画像データ全部に適用すればよいだけだ(poolMaxとpoolMax')。
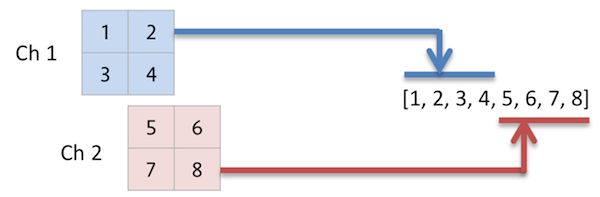
一次元化(FlattenLayer)
これは層というよりデータの整形だ。畳み込み層やプーリング層の出力は二次元平面、複数チャネルという、いわゆる「画像」の形をしているが、隠れ層では「一次元配列」を入力に取る。ということでその間に変換が必要なのだ。
(Image.hs)
flatten :: Image -> Image
flatten im = [[concat $ concat im]]
単に全チャネルの画素値を一列に並べているだけである。ただし、Layer型なので結果は「画像=3次元配列」にする必要がある。なのでわざわざ前後に2つの角カッコをつけて3元配列にみせかけている。
隠れ層(HiddenLayer)
これはいわゆる全結合層なのだが、他の記事やプログラムを見ると隠れ層という名で作られているのでそれに倣った。隠れ層としながら、最終の出力層もこのHiddenLayerを使っているので名前は変えるべきかもしれない。。。
この層では、入力(channel)c個を出力(kernel)k個に変換する。c個の要素全てがk個の各出力に関連付けられているため全結合というらしい。その関連付けをフィルタとして与える必要があるのでそのサイズは$c \times k$になる。初期はランダム値を設定し、学習によってその値を少しずつ補正することで画像認識などができるらしい。フィルタは$c \times k$の二次元リストで与えることにしよう。
(HiddenLayer.hs)
initFilterH :: Int -> Int -> IO [FilterH]
initFilterH k c = do
f <- forM [1..k] $ \i -> do
f' <- initKernel c
return f'
return f
where
a = 1.0 / fromIntegral c
initKernel :: Int -> IO FilterH
initKernel c = do
w <- forM [1..c] $ \i -> do
r <- MT.randomIO :: IO Double
return ((r * 2.0 - 1.0) * a)
return (0.0:w)
各要素は入力要素数cに対し$1/c$ ~ $-1/c$ の間の乱数としている。ただし、最初の要素はバイアス値で、初期値は0.0とするらしい。
この層では入力値にフィルタ値を掛けてすべて足しこむ(k個分)。式で書くとこうなる。なおフィルタの要素は $w_{ij}$ としている。
$
u_i = \sum_{j=0}^c w_{ij} x_j + b_i
$
ここで$x_j$は$j$番目の入力値、$u_i$は$i$番目の出力値、$b_i$は$i$番目の
バイアス値である。
実装はこう。
(HiddenLayer.hs)
connect :: [FilterH] -> Image -> Image
connect [] _ = error "invalid FilterH"
connect _ [] = error "invalid Image"
connect fs [[im]] = [[map (dot im) fs]]
where
dot :: [Double] -> [Double] -> Double
dot im f = sum $ zipWith (*) (1.0:im) f
dot関数のzipWith第一引数に1.0が追加されているのは先の$b_i$を足し込むためである(FilterHには$b_i$が含まれている)。
実行してみた
以上でひとまず順伝播については実装できた(と思う)。まずはコンパイル。
$ cd deeplearning
$ cabal configure
:
$ cabal build
:
では実行してみよう。
$ dist/build/deeplearning/deeplearning
Building the model...
Training the model...
iter = 0/200 time = 0s ratio = 0.0
iter = 5/200 time = 0.0030001s ratio = 0.33333713817332733
iter = 10/200 time = 0.333019s ratio = 0.33333713817332733
iter = 15/200 time = 0.682039s ratio = 0.33333713817332733
:
iter = 200/200 time = 13.0807482s ratio = 0.33333713817332733
Finished!
反復5回毎に状態を出力しており、左から
- epoch(反復回数)
- 経過時間(秒)
- 正解率
- 正解率は、全テストデータを順伝播にかけ得られた出力値から正解にあたる
要素の値(その要素が正解である確率)を取り出して平均したもの。 - 3種類に分類されるデータを使ったので何も学習していない状況だと
出力は均等割合となり約1/3になる。
- 正解率は、全テストデータを順伝播にかけ得られた出力値から正解にあたる
である。正解率は期待通り約1/3になっているものの、学習してないのでこの結果だけではなんとも言えない。ただ、何となくそれらしい出力が出てくると楽しい。
まとめ
前回から取り組んでいたCNN画像認識プログラムの「順伝播」のみ実装完了した。出力結果にはほとんど意味はないが、各層の処理を経てなんとなく結果が出力されたので雰囲気はつかめたかなと。
次回以降で本当のメインである学習処理を実装し「意味のある結果」が得られることを期待しよう。
(ここまでのソースはこちら)