Mediumの記事を読んでとても役に立ったのでメモしておきます。
まとめ
・時系列データを使った予測において、定常性(stationary)、季節性(seasonality)、自己相関(autocorrelation)に注意しなければいけない。
・主なモデル化手法として移動平均法、指数平滑法、ARIMA等がある。
・詳しく知りたい人用のチュートリアルはこちら
前置き
・トレンドや金融市場などの予測では"時間"が重要な要素となる。
・時系列データとは、時系列に沿って並んだデータのこと。
・時系列データにおいて、時間は説明変数(independent variable)である。
※説明変数:何かの原因となっている変数 ⇔ 目的変数:結果となっている変数。
(例)バネにおもりをつける事象の場合、説明変数は「おもりの重さ」、目的変数は「バネの伸び」となる。
・時系列データを使う目的は将来の予測。
・時系列データを利用する際の注意点として、定常性(stationary)、季節性(seasonality)、自己相関(autocorrelation)が挙げられる。
自己相関
・自己相関とは、時間差に応じて発生する観測点の間の類似性と言える。
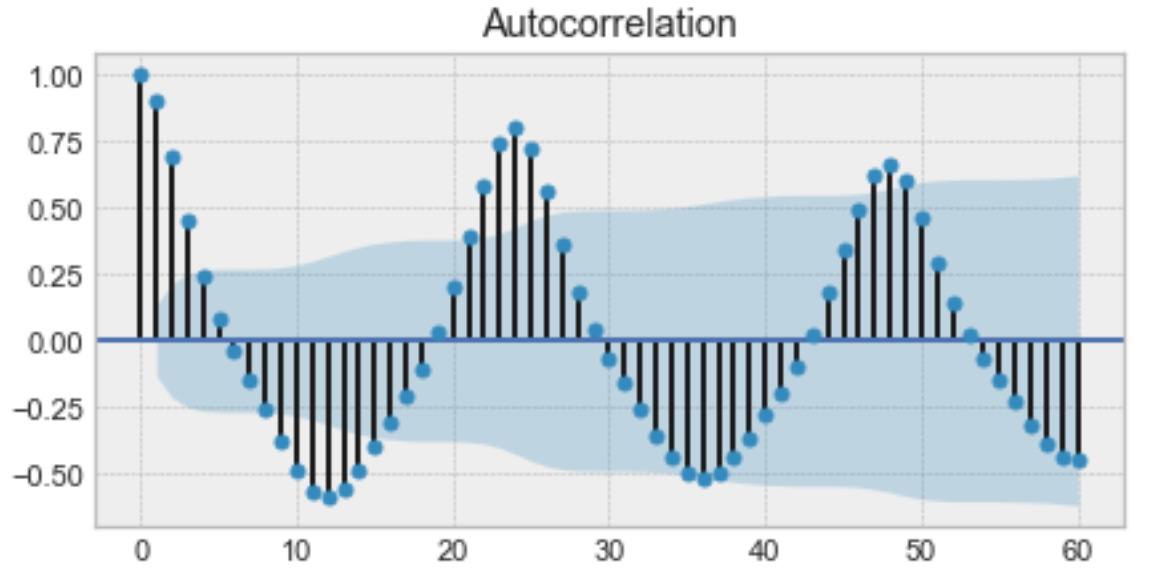
・この画像で、時刻0と時刻24、時刻12と時刻36などの関係を、自己相関が高いと言う。
・自己相関は季節性のヒントとなる。
季節性
・周期的な変動、のこと。例えば電気消費量は日中に増え夜間に減る、クリスマス前にネット販売は増える、など。
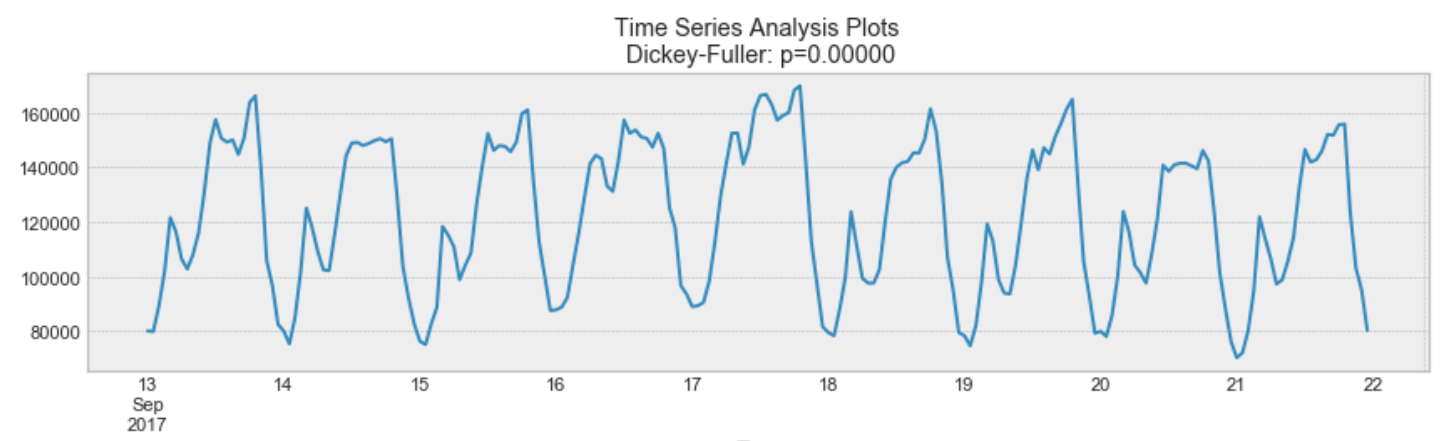
・これは明らかな季節性の時系列データ。夜間に向けてピークを迎え、日付が変わるころに最低となる。
・「自己相関が見られるデータの間隔」が季節の長さとなる。
定常性
・統計量が期間を通じて変化しないことを定常性と言う。つまり、平均と分散、共分散が時刻に依存しなければ定常性があると言える。

・これは平均も分散も大きく変動していないため、定常性がある時系列データである。
・株式価格の推移は定常性がないことがある。例えば上昇相場の場合やボラティリティが増加していく場合には、平均や分散が変動するため定常性がない。
・モデリングにおいては定常性のある時系列データがあることが理想的。
・全ての時系列データに定常性があるわけではないが、適切なデータの変換によって定常性を持たせることが出来る。
定常性の有無の検証方法
・Dickey-Fuller検定で定常性の有無を検証できる。これは単位根の有無を検証する仮設検定である。単位根が存在するのであれば定常性がない。
(参考)Wikipedia
・検定の帰無仮説は単位根が存在すること、対立仮説は単位根が存在しないこと。
・帰無仮説が棄却できない->単位根が存在する=定常性がない。
・帰無仮説が棄却できる->単位根は存在しない=定常性がある。
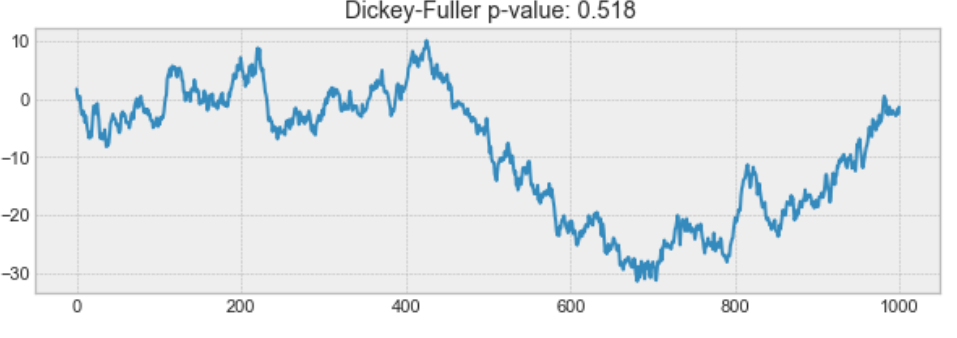
・これは平均が一定ではないため定常性がない。
時系列データのモデリング
・ここでは移動平均法、指数平滑法、ARIMA(Autoregressive, Integrated and Moving Average:自己回帰和分移動平均)を挙げる。
・移動平均法は最も単純で、過去データの平均を以って次のデータの予測値とするモデルのこと。単純だが、モデリングの入り口としては良く、トレンドの発見にも使える。
・(単純)指数平滑法は移動平均法と似ているが、予測時点から離れたデータほど重みを小さくし、遠い過去のデータの重要性を小さくしている。
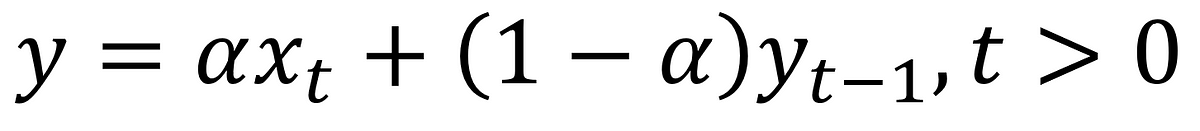
・数式で表すとこのようになる。αは平滑化定数で、古いデータの重要性をどれだけ早く減らすかを決定する(αが0に近づくと移動平均法へ近づく)。
・二重指数平滑法は、指数平滑を二回繰り返したモデル。
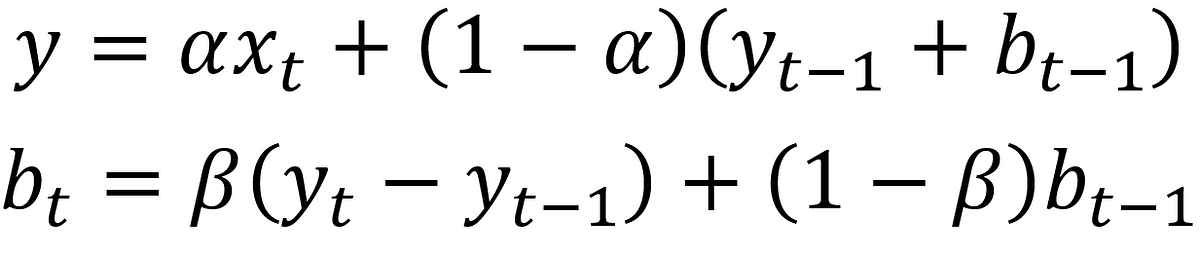
・上記式が二重指数平滑法を表しており、βはトレンド平滑化定数。
・三重指数平滑法は、更に季節性平滑化定数(※)を追加したモデル。
(※正しい日本語訳か自信ないです)
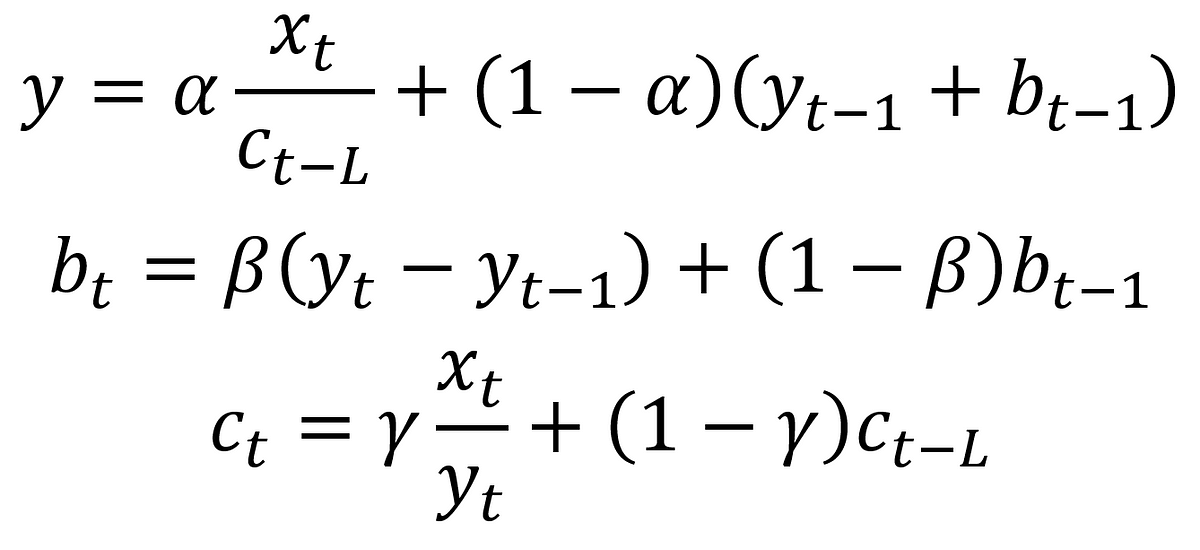
・季節性をモデリングすることが出来る。
・SARIMA(Seasonal autoregressive integraded moving average model )は自己回帰モデル(AR(p)モデル)と季節性を組み合わせたモデル。
・詳しく知りたい人はこちらのチュートリアル参照。
所感
証券アナリストの勉強をしていて時系列データ分析のさわりが出てきたことを思い出した。当時は理論的な部分をざっくり学習しただけだったが、せっかくチュートリアルを見つけたので次はコーディングをしてみようと思う。