2線分の交差判定手法 (2次元)

AtCoderで遊んでいたところ「このような問題」に出くわした。
そこで同一平面上に存在する2線分の交差判定手法について調査した。

#線分が交差する条件
線分 $AB$ と線分 $CD$ について考える。

(1) 点 $A$ 点 $B$ を含む直線 $AB$ を境界線として平面を分割するとき、点 $C$ 点 $D$ がそれぞれ別の領域に存在
(2) 点 $C$ 点 $D$ を含む直線 $CD$ を境界線として平面を分割するとき、点 $A$ 点 $B$ がそれぞれ別の領域に存在

(1), (2)の条件を共に満たすとき線分 $AB$ と線分 $CD$ は交差する。

#点の存在する領域
点 $P$ が平面を分割する直線に対してどちらの領域に存在するかは、直線の方程式に点 $P$ の座標を代入した値の正負で判定ができる。

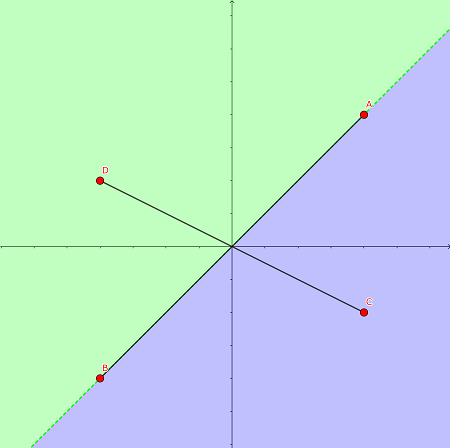
例えば、直線 $x - y = 0$ に対する点 $C$ $(4, -2)$ の存在する領域を調べる場合
$x - y$ に $(x, y) = (4, -2)$ を代入すると $x - y = 6$ $(> 0)$

一方、直線 $x - y = 0$ に対する点 $D$ $(-4, 2)$ の存在する領域を調べる場合
$x - y$ に $(x, y) = (-4, 2)$ を代入すると $x - y = -6$ $(< 0)$

点 $C, D$ で得られる値の正負が異なるため、点 $C, D$ は別の領域に存在することがわかる。

つまりこの判定を

• 直線 $AB$ に対する点 $C, D$
• 直線 $CD$ に対する点 $A, B$

で行えば線分の交差判定ができる。
(線分の端点が別の線分上に存在する場合に注意)

#線分の交差判定を行うアルゴリズム
まず点 $A$ $(x_A, y_A),$ 点 $B$ $(x_B, y_B)$ を含む直線 $AB$ の方程式を求める。

直線 $AB$ の傾きは $\frac{y_A - y_B}{x_A - x_B}$

直線 $AB$ は点 $A$ を含むため、直線 $AB$ の方程式は $y - y_A = \frac{y_A - y_B}{x_A - x_B} (x - x_A)$

式を変形すると $(x_A - x_B)(y - y_A) - (y_A - y_B)(x - x_A) = 0$

したがって点 $C$ $(x_C, y_C),$ 点 $D$ $(x_D, y_D)$ の領域判定を行う場合

$s = (x_A - x_B)(y_C - y_A) - (y_A - y_B)(x_C - x_A)$
$t = (x_A - x_B)(y_D - y_A) - (y_A - y_B)(x_D - x_A)$

とおくと $st<0$ の時、点 $C, D$ は直線 $AB$ に対して別の領域に存在するといえる。

上記のアルゴリズムをC++で記述した例を以下に示す。

typedef struct Point_Coordinates {
	double x, y;
} point;

// 線分ab, cdが交差する場合True
// 端点が他方の線分上にある場合もTrue
// 端点が他方の線分の延長線上にある場合もTrueを返すので注意
int Judge(point &a, point &b, point &c, point &d) {
	double s, t;
	s = (a.x - b.x) * (c.y - a.y) - (a.y - b.y) * (c.x - a.x);
	t = (a.x - b.x) * (d.y - a.y) - (a.y - b.y) * (d.x - a.x);
	if (s * t > 0)
		return false;

	s = (c.x - d.x) * (a.y - c.y) - (c.y - d.y) * (a.x - c.x);
	t = (c.x - d.x) * (b.y - c.y) - (c.y - d.y) * (b.x - c.x);
	if (s * t > 0)
		return false;
	return true;
}

#外積を用いる方法
ここまで直線の方程式を用いて領域判定を行ってきたが、外積を用いると簡単に判定を行うことができる。

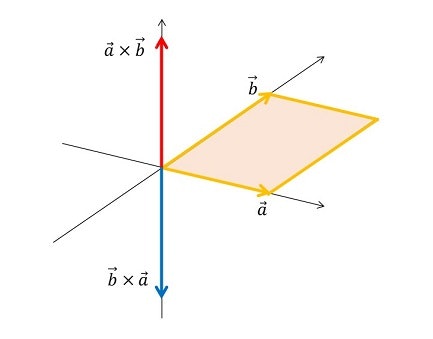
2次元平面においてベクトル $\vec{a}, \vec{b}$ の外積 $\vec{a} \times \vec{b}$ は $\vec{a}$ から $\vec{b}$ への右ねじの方向を符号に持つスカラー値となる。
したがって線分 $AB, CD$ の交差判定を行う場合

$s = \vec{AB} \times \vec{AC} = (x_B - x_A)(y_C - y_A) - (x_C - x_A)(y_B - y_A)$
$t = \vec{AB} \times \vec{AD} = (x_B - x_A)(y_D - y_A) - (x_D - x_A)(y_B - y_A)$

とおくと $st<0$ の時、点 $C, D$ は直線 $AB$ に対して別の領域に存在するといえる。
またこの $st$ の値は 線分の交差判定を行うアルゴリズム と同じ値を取ることがわかる

#まとめ
一見異なる求め方でも同じ式が導かれるの面白い