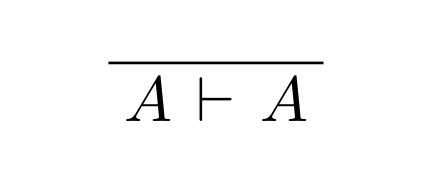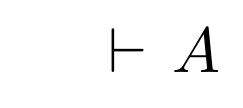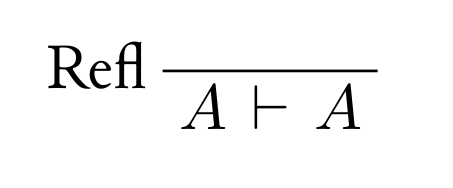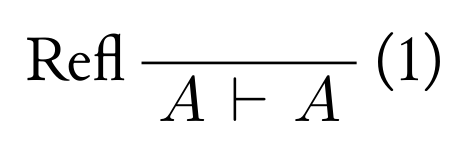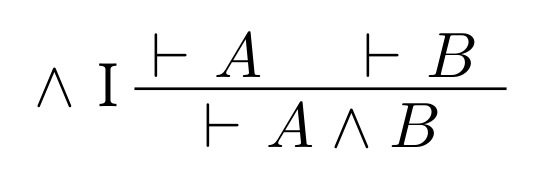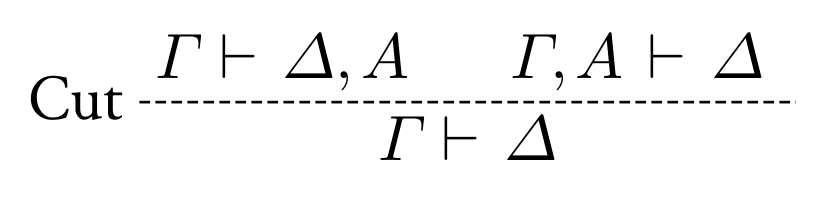⚠ この記事は最新の機能を反映していません。SATySFi の導出木描画ライブラリ satysfi-derive を参照してください。
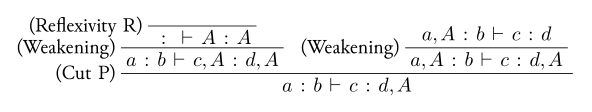
ひとこと: ↑こういう導出木が↓こういう感じのコードで書けるようになる
\proven!(
open DeriveDSL in
derive ${ \biseq{a}{b}{c}{d, A} }
|> by {(Cut P)}
|> from [
derive ${ \biseq{a}{b}{c, A}{d, A} }
|> by {(Weakening)}
|> from [
derive ${ \biseq{\void}{\void}{A}{A} }
|> by {(Reflexivity R)}
];
derive ${ \biseq{a, A}{b}{c}{d, A} }
|> by {(Weakening)}
|> from [
assume ${ \biseq{a, A}{b}{c}{d} }
]
]
)
証明論や型システムについての記事を書いていると、しばしば導出木を書く必要がでてきます。Latexだと bussproof あたりがよく使われている気がします。bussproof は組版の品質は上々なんですが、導出木の記述に独自のスタック指向のDSLを使っていて、読んだり変更を加えたりするのが少々面倒くさかったりします。
そこで SATySFi です。フルのプログラミング言語が使える組版システムであるところの SATySFi であれば、導出木をわかりやすく記述するためのDSLを作れそうです。実際にそれらしいものができたので、この記事で紹介します。
注: SATySFiの標準ライブラリは Proof モジュールを提供していてそちらでも導出木を書くことができます。Proofとの比較は今は割愛します。
インストール
今回の成果物は satysfi-lib におかせてもらっています。同じディレクトリに satysfi-lib をクローンした場合なら、以下のような import を書くだけで準備完了です。
@import: satysfi-lib/typeset/derive
% enjoy derive!
使い方
この import によって二つのモジュールが使えるようになります。
-
Derive: 導出木を書くための数式コマンド\provenのみを提供 -
DeriveDsl:\proven中で導出木を構築するためのDSLを提供
モジュールを二つに分けているのは、DeriveDsl が衝突しやすそうな名前を多用しているためです。以下のような感じでDeriveはさっさと open する一方で、DeriveDSLは \proven 内の必要な部分だけで open するのが無難です。
@import: satysfi-lib/typeset/derive
open Derive in
% ....
+math (${
\proven!(
open DeriveDSL in
% Write DSL here
)
});
% ....
Derive モジュール
\proven : [derivation-ast] math-command
\proven コマンドは導出木を表示するための数式コマンドです。導出木を表すデータ derivation-ast を受け取ってレンダリングします。
${
\proven!(
% Write DSL here
)
}
!(...)は数式モードからプログラムに切り替える構文で、この中でDSLを書いて derivation-ast のデータを構築します。
DeriveDsl モジュール
DeriveDsl モジュールは derivation-ast を構築するための複数の関数から成ります。
derive : math -> derivation-ast
derive は導出木を構築する上で最も基本的な関数です。数式を一つうけとって1.前件がなく 2.ラベルもなく 3.区切り線が普通の線の 導出木をつくります。
open DeriveDSL in
derive ${A \vdash A}
derive の亜種で assume があります。これは基本的には derive と同じですが、導出の線が表示されません。
open DeriveDSL in
assume ${\vdash A}
by : inline-text -> derivation-ast -> derivation-ast
by は導出にラベルを加える関数です。ラベルはinline-textで与えます。
open DeriveDSL in
by {Refl} (derive ${ A \vdash A })
上のように書くこともできますが、以下のようにパイプライン演算子を使うとコードがぐっと綺麗になります。
open DeriveDSL in
derive ${ A \vdash A }
|> by {Refl}
どちらにせよ以下のようにレンダリングされます。
同様の関数にbyOpがあります。ラベルはデフォルトで左側に表示されますが、byOpは反対側にラベルを表示します。
open DeriveDSL in
derive ${ A \vdash A }
|> by {Refl}
|> byOp {(1)}
from : derivation-ast list -> derivation-ast -> derivation-ast
from は導出に前提を追加する関数です。from dlist d で 「dlist の各導出から d を導く導出」を構築します。
open DeriveDSL in
derive ${ \vdash A \wedge B }
|> by {${\wedge} I}
|> from [
assume ${\vdash A};
assume ${\vdash B}
]
withLine : derivation-line -> derivation-ast -> derivation-ast
withLine は導出の線を変更するための関数です。
今のところ derivation-line の値を作る方法は以下の3つです。
-
standard-line:derivation-line- 直線
-
no-line:derivation-line- 線なし
-
dotted-line:length -> length -> derivation-line-
dotted-line a bで「黒線がa、空白がbが繰替えされる点線」を表す
-
standard-line と no-line は derive と assume で代用できるので実質的には dotted-line のための関数かもしれません。(あるいは「線はいらないけどassumeって感じではないんだよなあ」という時にも使えます)
open DeriveDSL in
derive ${ \Gamma \vdash \Delta }
|> by {Cut}
|> withLine (dotted-line 2pt 1pt)
|> from [
assume ${\Gamma \vdash \Delta, A};
assume ${\Gamma, A \vdash \Delta}
]
応用編 : デフォルトの設定を変える
実は \Derive.proven は一つオプショナル引数をとります。
val \proven : [derive-config?; derivation-ast] math-cmd
この derive-config を明示的に渡すことでデフォルトの様々な設定を変えることができます。
-
byによるラベルが右に置かれるか左に置かれるか -
deriveで表示されるデフォルトの線 - その他導出木のレンダリングの細かい設定
まだこのあたりの設計は煮詰まっていないのでまた後日記事を書きます……
まとめ
satysfi-lib を使うといい感じに導出木を書けるよ。