FitzHugh-Nagumo方程式をオイラー法で数値計算する

FitzHugh-Nagumo方程式とは

wikiより

フィッツフュー-南雲モデル(FitzHugh-Nagumo model)は、神経細胞などの電気的興奮性細胞の活動電位を表現したモデルであり、リチャード・フィッツフューと南雲仁一の名にちなんでいる。このモデルは、神経細胞の活動電位発火(スパイク)における活性化と不活性化をモデル化したホジキン-ハクスリーモデル の微分方程式を簡略化したものである。フィッツフュー-南雲モデルは以下のように僅か2つの微分方程式で表される。
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%83%E3%83%84%E3%83%95%E3%83%A5%E3%83%BC-%E5%8D%97%E9%9B%B2%E3%83%A2%E3%83%87%E3%83%AB

\frac{dX}{dt}=c(X-X^3-Y)
\\
\frac{dY}{dt}=X-bY+a

オイラー法で近似

X(t+Δt)= X(t)+\frac{dX}{dt}Δt
\\
Y(t+Δt)=Y(t)+\frac{dY}{dt}Δt

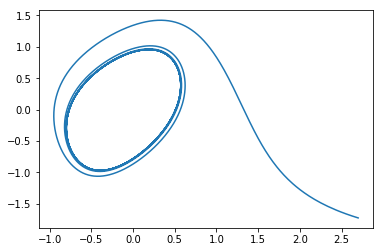
結果は以下の画像のようになります。初期値(X,Y)=(0,0)をスタートして楕円形のアトラクターに引き込まれているのが確認できますね。
(ただし、a=0.01, b=0.5, c=1.0)

コード全文(jupyter推奨)

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sbn
from numpy.random import *
N = 10000
dt = 0.01

def calc(a,b,c, X, Y):
    x.clear()
    y.clear()
    for i in range(N):
        X += (c*(X-X**3-Y))*dt
        Y += (X-b*Y + a)*dt
        x.append(X)
        y.append(Y)
    return x, y

# ここのパラメータをいじって遊ぶ
calc(0.1, 0.3, 0.5, 10*(rand()-0.5), 10*(rand()-0.5))
plt.plot(x,y)
plt.show()
plt.plot(x)
plt.plot(y)

初期値を変化させて収束性を確認