なぜ、実装してみたのか
ずっと昔の話なのですが、.net 2.0以前ではコレクションクラスの数が少なく、ソート済みリストをプログラムで使用するには SortedList しか選択肢がありませんでした。
SortedListは期待どおりソート済みのリストを提供してくれるのですが、如何せんデータ構造が配列であるため、ランダムな値の追加を繰り返すと、並び替え時に値が挿入、移動されてパフォーマンスの劣化がひどいものでした(当時は 1万件こえるなら、ArrayListにして追加後にソートとして処理していたほうが良かったと覚えています)
そのため、何か良いアルゴリズムはないものかと調査して、シーケンシャルアクセスの容易さから B+木を選択実装してみました。
ソースコード
上記の理由のとおり、元々はずっと昔の Visual Basicのコードを焼き直したものになります。別に C/C++ 版もありますが、しばらく公開はしないでしょう。
当時の知識での実装であり、コンバートでもあるため、間違いもあるのでしょうが、許してください。
ソースは GitHub にアップロードしています(同梱されている Deckクラスは別の目的で用意したものなので本文章と無関係です)
特徴として
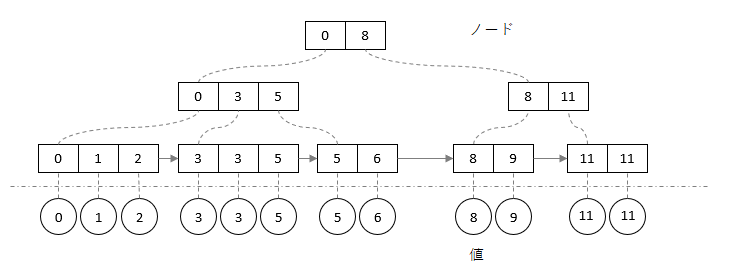
B+木はシーケンシャルな要素アクセスに強みを持っています。それは値を持つノードとノードを持つノードが区別されていて、値を持つノードがリンクリストで表現されているためです。{0,1,2,3,3,5,5,6,8,9,11,11} という値を格納した B+木は以下の図のようになります。
値は〇で表現しています。図で示すとおり、値は木構造の最下層のみに紐付いており最下層のノードは同じ最下層のノードとリンクしています。リンクを辿ることでシーケンシャルなアクセスを表現できるのです。
詳細な B+木のアルゴリズムについてはWiki等参照いただければと思います。
使い分けのための比較
現在の .net 標準コレクションでは SortedList、SortedDictionary、SortedSet があります。
今回実装した B+木コレクションは上記のコレクションとは以下の違いを持たせています。
- 同じ値を複数格納できます
- 指定した値を基準に値を列挙できるイテレータを持っています
- より大きい、より小さい、以上、以下の検索を行えます
- 指定した値より大きい(最初の値から検索し指定値より大きい)位置を検索
- 指定した値以上(最初の値から検索し指定値以上)位置を検索
- 指定した値より小さい(最後の値から検索し指定値より小さい)位置を検索
- 指定した値以下(最後の値から検索し指定値以下)位置を検索
性能について
性能について、簡単な比較を以下のコードで行ってみました。
(実際に使用する場合はメモリの使用量など別の要件もあるので、参照程度と意識してください)
(実行環境は core i5-8250U 1.6GHzです)
int limit = 1000000;
// 使用する値をランダムに並び替える
var rnd = new Random();
var vals = new List<int>();
for (int i = 0; i < limit; ++i) {
vals.Add(i);
}
for (int i = 0; i < vals.Count - 1; ++i) {
var idx = rnd.Next(vals.Count - 1 - i);
var tmp = vals[vals.Count - 1];
vals[vals.Count - 1] = vals[idx];
vals[idx] = tmp;
}
// SortedSet
var sw = new Stopwatch();
Console.WriteLine("〇 SortedSet");
Console.WriteLine("・ 追加");
sw.Start();
var sorted = new SortedSet<int>();
foreach (var v in vals) {
sorted.Add(v);
}
sw.Stop();
Console.WriteLine($"{sw.Elapsed.TotalSeconds}sec");
Console.WriteLine("・ 削除");
sw.Restart();
foreach (var v in vals) {
sorted.Remove(v);
}
sw.Stop();
Console.WriteLine($"{sw.Elapsed.TotalSeconds}sec");
// BPlusTree
Console.WriteLine("〇 BPlusTree");
Console.WriteLine("・ 追加");
sw.Restart();
var tree = new BPlusTree<int>();
foreach (var v in vals) {
tree.Add(v);
}
sw.Stop();
Console.WriteLine($"{sw.Elapsed.TotalSeconds}sec");
Console.WriteLine("・ 削除");
sw.Restart();
foreach (var v in vals) {
tree.Remove(v);
}
sw.Stop();
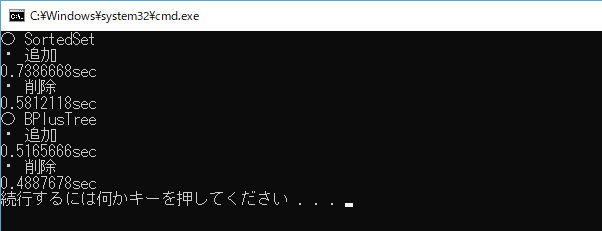
Console.WriteLine($"{sw.Elapsed.TotalSeconds}sec");
追加と削除はSortedSet に負けてないですね。
効率的なアルゴリズムを調査、パフォーマンスチューンを行えば、もっと良くなるかもしれません。
最後に
このようなデータ構造は、知識の引き出しとして幾つか持っておくと便利です。
記憶の片隅にとっておいて下さい。