■ はじめに
今回は、線形回帰・Ridge回帰・Lasso回帰における
各特徴と違いについて、記事をまとめさせていただきます。
■ モジュール・データの準備
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, Lasso
from sklearn.linear_model import RidgeCV
from yellowbrick.regressor import AlphaSelection
mglearnとは、データの使用やプロットを視覚化するためのモジュールです。
今回は改良版のbostonデータセットを使用します。
元データと異なり、特徴量は104個となります。
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
print('X:', X.shape)
print('y:', y.shape)
print('X_train:', X_train.shape)
print('y_train:', y_train.shape)
print('X_test:', X_test.shape)
print('y_test:', y_test.shape)
# X: (506, 104)
# y: (506,)
# X_train: (379, 104)
# y_train: (379,)
# X_test: (127, 104)
# y_test: (127,)
1. 線形回帰
lr = LinearRegression().fit(X_train, y_train)
# 決定係数(回帰モデルの予測の正確さを測る指標)
print('Train set score: {}'.format(lr.score(X_train, y_train)))
print('Test set score: {}'.format(lr.score(X_test, y_test)))
# Train set score: 0.9520519609032729
# Test set score: 0.6074721959665842
scoreは、決定係数(回帰モデルの予測の正確さを測る指標)です。
線形回帰において、手元にある訓練データの予測の精度は高いですが
テストデータ(未知のデータ)に対しては、予測の精度が低くなる傾向があります。
スポーツ(野球)に例えると、普段からストレートの球ばかり打つ練習をしていたために
本番の試合では、カーブの球に全く対応できなくなってしまうといった感じでしょうか。
実務やKaggleでは、未知のデータに対する汎化性能(本番への対応力)が重要となるため
今回のデータの場合、線形回帰モデルは不向きであることが分かります。
2. Ridge回帰
先ほどのような、訓練データに適応しすぎて
テストデータへの汎化性能が落ちることを「過学習」といいます。
これを防ぐために、Ridge回帰で正則化(パラメータ:alpha)を行います。
回帰係数(各特徴量の値)が大きくなったり、ばらつきがあると過学習が起こりやすくなりますが
パラメータのalphaを大きくすると、回帰係数は0に近づいていきます。
ridge = Ridge(alpha=1).fit(X_train, y_train)
print('Training set score: {}'.format(ridge.score(X_train, y_train)))
print('Test set score: {}'.format(ridge.score(X_test, y_test)))
# Training set score: 0.885796658517094
# Test set score: 0.7527683481744752
訓練データへの適応は低下しますが、テストデータへの汎化性能は向上しました。
Ridge回帰のalphaはデフォルトで1となっているので、他の値でも試してみます。
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print('Training set score: {:.2f}'.format(ridge10.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(ridge10.score(X_test, y_test)))
# Training set score: 0.79
# Test set score: 0.64
alpha=1のときよりも、テストデータへの予測精度が低下しました。
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print('Training set score: {}'.format(ridge.score(X_train, y_train)))
print('Test set score: {}'.format(ridge.score(X_test, y_test)))
# Training set score: 0.885796658517094
# Test set score: 0.7527683481744752
こちらは、alpha=1のときと同じくらいの予測精度となります。
ここで、各回帰係数の大きさとばらつきについて
alpha=0.1, 1, 10の、3パターンを比較をしてみます。
plt.plot(ridge10.coef_, 's', label='Ridge alpha=10')
plt.plot(ridge.coef_, 's', label='Ridge alpha=1')
plt.plot(ridge01.coef_, 's', label='Ridge alpah=0.1')
plt.plot(lr.coef_, 'o', label='LinearRegression')
plt.xlabel('Coefficient index')
plt.ylabel('Coefficient magnitude')
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()
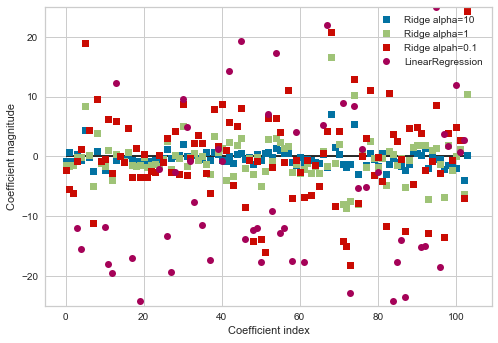
横軸:104個の特徴量
縦軸:モデルにおける各回帰係数の大きさ
alpha=0.1, 1のように、データにある程度のばらつきがあった方が、スコアは高いことが分かります。
しかし線形回帰のようにばらつきが大きすぎたり(過学習)、alpha=10のように正則化を強くしすぎてしまうと
決定係数のスコアは低くなってしまいます。
先ほどはいくつかのalphaを代入してスコアの比較を行いましたが
最適なalphaについて、事前に調べる方法もあります。
まずパラメータalphaについて、値の探索する範囲を設定し
RidgeCVで訓練データについて交差検証を実行、AlphaSelectionで最適な値を求めプロットします。
alphas = np.logspace(-10, 1, 500)
ridgeCV = RidgeCV(alphas = alphas)
alpha_selection = AlphaSelection(ridgeCV)
alpha_selection.fit(X_train, y_train)
alpha_selection.show()
plt.show()
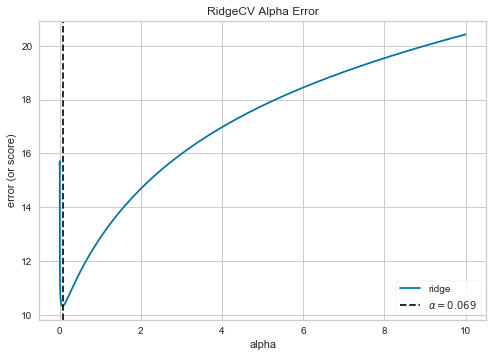
これにより、今回のRidge回帰における最適なパラメータ(alpha)の値が分かりました。
ridge0069 = Ridge(alpha=0.069).fit(X_train, y_train)
print('Training set score: {}'.format(ridge.score(X_train, y_train)))
print('Test set score: {}'.format(ridge.score(X_test, y_test)))
# Training set score: 0.885796658517094
# Test set score: 0.7527683481744752
実際に試してみると、alpha=0.1, 1の時と同じ、高いスコアとなりました。
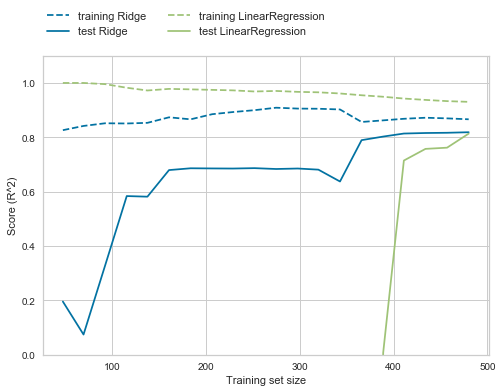
次に、線形回帰とRidge回帰(alpha=1)の比較として、学習曲線をプロットしてみます。
mglearn.plots.plot_ridge_n_samples()
線形回帰では過学習を起こしやすいため、訓練データのスコアは高いですが
テストデータにおいては、汎化性能がほぼゼロとなってしまっています。
ただし、データサイズが十分にあれば
Ridge回帰と同程度の汎化性能を持つことが分かります。
3. Lasso回帰
Ridge回帰と同様に、係数が0に近づくように制約をかけますが
かけ方が少し異なり、Lasso回帰はいくつかの係数が完全にゼロとなります。
Number of features used:使用した特徴量の数
lasso = Lasso().fit(X_train, y_train)
print('Training set score: {:.2f}'.format(lasso.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(lasso.score(X_test, y_test)))
print('Number of features used: {}'.format(np.sum(lasso.coef_ != 0)))
# Training set score: 0.29
# Test set score: 0.21
# Number of features used: 4
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print('Traing set score: {:.2f}'.format(lasso001.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(lasso001.score(X_test, y_test)))
print('Number of features used: {}'.format(np.sum(lasso001.coef_ != 0)))
# Traing set score: 0.90
# Test set score: 0.77
# Number of features used: 33
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print('Training set score: {:.2f}'.format(lasso00001.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(lasso00001.score(X_test, y_test)))
print('Number of features used: {}'.format(np.sum(lasso00001.coef_ != 0)))
# Training set score: 0.95
# Test set score: 0.64
# Number of features used: 96
重要度の低い特徴量が0になりやすいように設計された誤差関数をもとに
訓練を行い、実際に使用する特徴量を決定しています。
今回の場合は、特徴量数が96個のように多かったり、4個のように少なすぎると
汎化性能が低くなっていることが分かります。
Lasso(alpha=0.0001)とRidge(alpha=1)について
回帰係数の大きさとばらつきを比較してみます。
plt.plot(lasso.coef_, 's', label='Lasso alpha=1')
plt.plot(lasso001.coef_, '^', label='Lasso alpha=0.01')
plt.plot(lasso00001.coef_, 'v', label='Lasso alpha=0.0001')
plt.plot(ridge01.coef_, 'o', label='Ridge alpha=0.1')
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel('Coefficient index')
plt.ylabel('Coefficient magnitude')
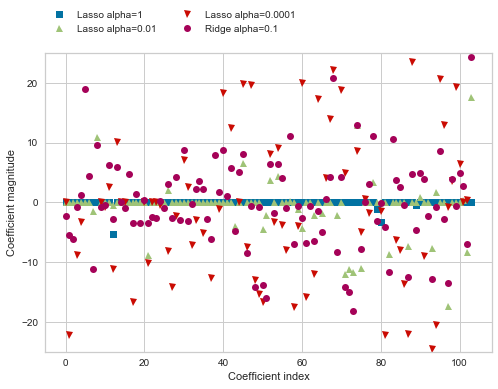
横軸:104個の特徴量
縦軸:モデルにおける各回帰係数の大きさ
上図を見ると、やはり係数のばらつきもある程度は必要であり
Lasso(alpha=0.0001)はRidge(alpha=1)と同程度散らばっているので
決定係数のスコアも近しいことが分かります。
■ 結論
線形回帰を考えるのであれば、まずはRidge回帰でモデリングをして
不要な特徴量などがあると分かれば、Lasso回帰を行ってみるのが良い。
ElasticNet(RidgeとLassoの両方のパラメータを持つ)は精度では優れますが、調整に手間がかかります。