まえがき
ふと幅優先探索と比べながらダイクストラ法を考えてみたらとてもしっくりきたので、記事に残したいなと思い、書いています。今までは、恥ずかしながらダイクストラ法はいまいち直感的にしっくりこず、知識として覚えて使っていました。
三角関数の公式を丸暗記せず、問題用紙の隅に単位円を書いて考えていたようなあなた (や、わたし) には、このように見方を変えてみるとひょっとしたら覚えやすいかもしれないです。
この記事で扱うこと
幅優先探索の復習をし、幅優先探索に「ある高速化テク」を適用しようとすると自然にダイクストラ法が導かれることを、なるべく直感的に説明します。
この記事で扱わないこと
「ダイクストラ法が必ず最短経路を見つける」こと、「ダイクストラ法が見つけた経路が必ず最短経路である」ことなどの厳密な説明はこの記事では扱いません。
前知識:幅優先探索とダイクストラ法の使い分け
大前提として、幅優先探索とダイクストラ法がそれぞれどんな場面で使えるアルゴリズムだったかを復習しておきます。
幅優先探索は一種の探索(条件を満たす項目を探す)アルゴリズムとして使うこともありますが、「あるスタート地点から各地点までの最短距離(経路)を求める」アルゴリズムとしても使うことができます。ただし、各地点どうしを結ぶ道の長さ(コスト)はすべて一定である必要があります。
対してダイクストラ法は、道にそれぞれ異なる長さ(コスト)が設定されていても使うことができる最短経路アルゴリズムです。
幅優先探索の復習
この記事では、まず幅優先探索について復習し、その亜種としてダイクストラ法を理解しようとしてみます。
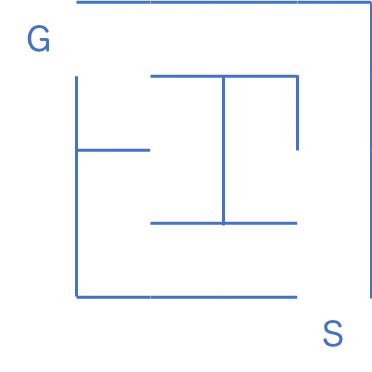
まずは幅優先探索の典型的なユースケースである、迷路の最短経路を求める問題を考えます。
幅優先探索では、スタート地点から近い順に各地点までの最短経路を確定させてゆくのでした。
初期化
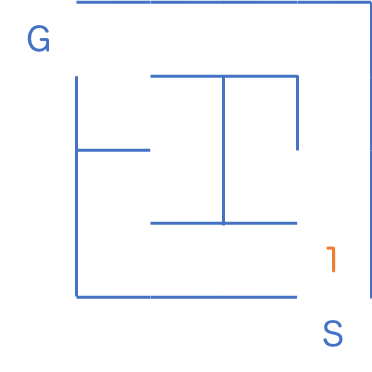
スタート地点から最初のマスまでの距離は1なので、 1 と書いておきます (問題によっては 0 かも)。
擬似コード:
cost[<スタート>] = 1
各マスを近い順に訪問
初期化できたら、ゴールへの最短経路が確定するまで、以下を繰り返します:
- 未訪問のマスのうち、一番小さい最短距離が書いてあるマスを探す
- そのマスを訪問済みにする
- 隣接するマスたちに最短距離を書き込む
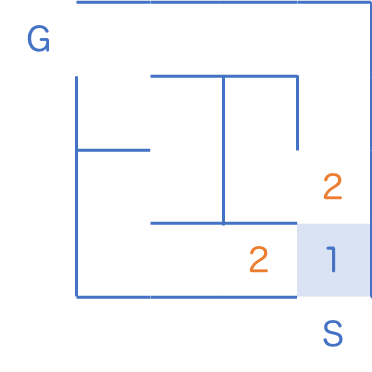
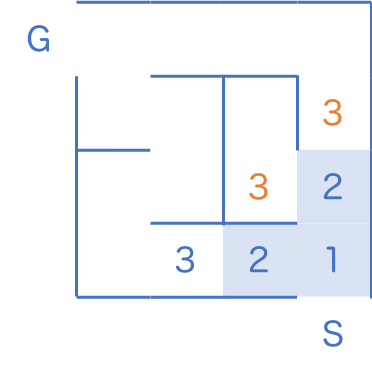
はじめ最短距離が書いてあるマスはスタート地点の 1 だけなので、まずはこのマスを訪問します (訪問済みになったことを、水色の背景で表すことにします)。 1 の周囲のマスには、スタート地点から数えて 2 歩でたどり着くことができるとわかるので、 2 と書いておきます。
最短距離が 1 のマスを見終わったので、次は2つある 2 のマスたちを見てゆきます。どちらを先に訪問しても構いません。
ここで、後戻りはしないことに注意してください。すなわち、すでに 1 と書いてあるマスに、上から 3 と書く必要はありません。
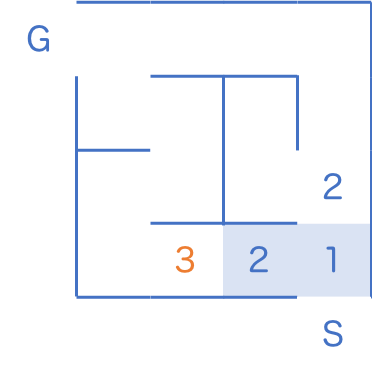
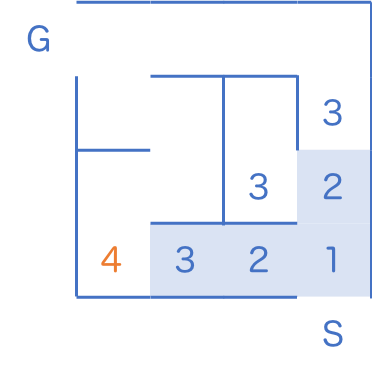
3 のマスが登場しましたが、 2 のマスがまだ残っているのでこちらを先に訪問します。
2 のマスを全て訪問し終えた時点で、初めて 3 のマスに手をつけます。
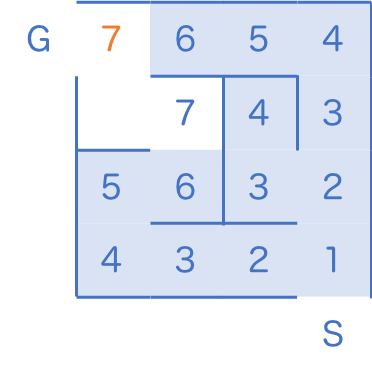
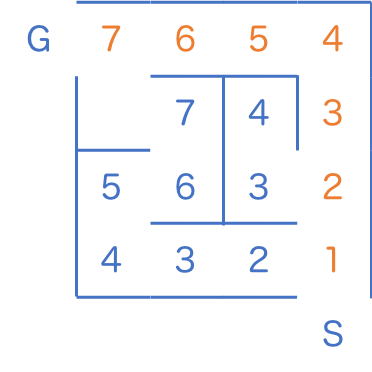
以下同様に進めてゆくと、最短 7 歩でゴールにたどり着くことがわかりました。
擬似コード:
def 次のマスを探す():
(minCost, minCell) = (∞, null)
for d in <全てのマス>:
if !visited[d]: # 未訪問のマス
if defined cost[d] && cost[d] < minCost: # 書いてあるコストがより小さい
(minCost, minCell) = (cost[d], d)
visited[minCell] = true
return minCell
while !defined cost[<ゴール>]: # ゴールのコストが判明するまで
d = 次のマスを探す()
for d2 in dに隣接するマスたち:
if !defined cost[d2]: # まだコストが書いてない
cost[d2] = cost[d] + 1
キューを使った最適化
上の擬似コードの計算量は、
- 次に訪問するマスを選ぶのに
O(n)[nはマスの数] - 訪問しなければいけないマスの数
O(n)
なので全体として O(n^2) になっています。これはキュー (先入れ先出しリスト) を使うことで改善できるのでした。
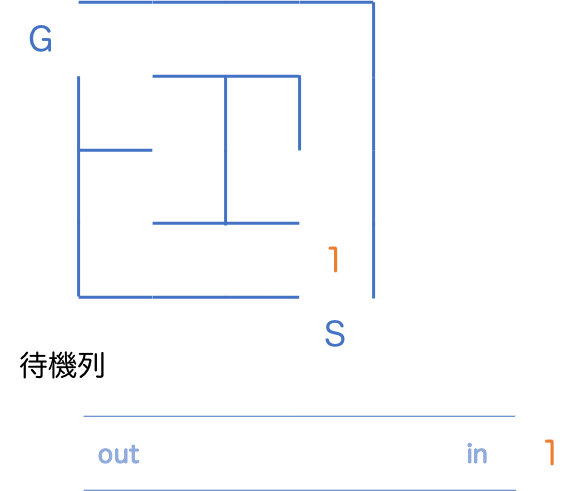
すなわち、新しく見つかったマスをいつも待機列の一番後ろに並ばせておけば、あとは列の先頭から順番に取り出していくだけで、自然と最短経路の短い順に訪問できます。いちいち次に訪問するマスを検索する必要はありません。
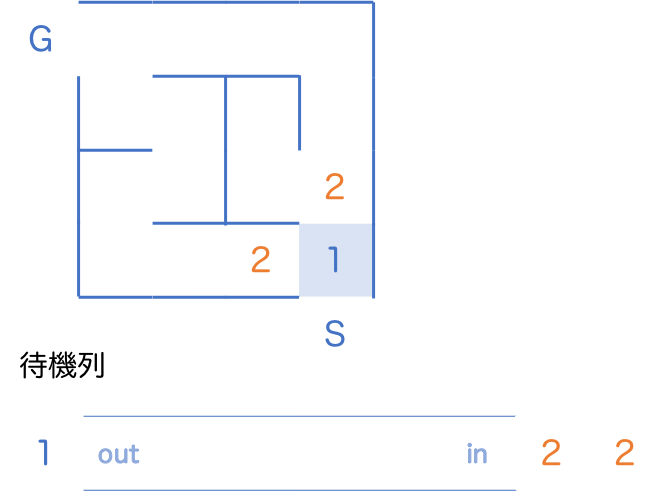
スタート地点の最短距離を 1 とし、待機列に並ばせます。
待機列の先頭にいた 1 を取り出し、新しく見つかった2つの 2 を待機列に並ばせます。
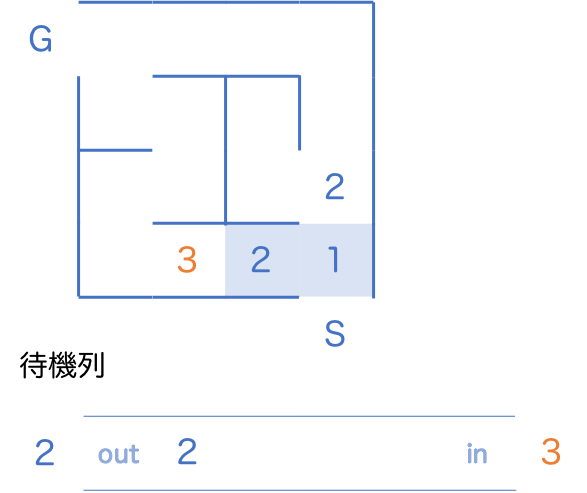
同様に待機列の先頭にいた 2 を取り出し、新しく見つかった 3 を待機列に並ばせます。
擬似コードは以下のように変わります:
while !defined cost[<ゴール>]: # ゴールのコストが判明するまで
- d = 次のマスを探す()
+ d = キューの先頭を取り出す()
for d2 in dに隣接するマスたち:
if !defined cost[d2]: # まだコストが書いてない
cost[d2] = cost[d] + 1
+ キューの末尾に加える(d2)
キューの追加・削除は一瞬 (O(1)) でできるので、計算量は O(n) に減りました。
これが一般的に用いられる幅優先探索です。
おまけ:経路の復元
最短距離だけでなく具体的な経路まで必要な場合には、ゴールからはじめて、「数字が1づつ下がっていくように」隣り合うマスを選んでいけば経路を復元できます。
ゴールの 7 から初めて、隣の 6 を探し、またその隣の 5 を探し… といった要領です。そのような経路が複数ある場合は、どれを選んでも最短経路になります。寄り道をしようとすると、必ず数字が増えてしまうはずです。
(「どのマスから来たか」を記録しながら探索していくとより高速に経路を復元することができますが、いよいよ本題から外れるので他の記事を参照してください)
幅優先探索からダイクストラ法を導く
幅優先探索の復習ができたところで、今度はダイクストラ法について考えてゆきます。
「幅優先探索で解く問題」と「ダイクストラ法で解く問題」の相互変換
上の迷路は、
・スタート
・ゴール
・分岐 / 合流地点
・行き止まり
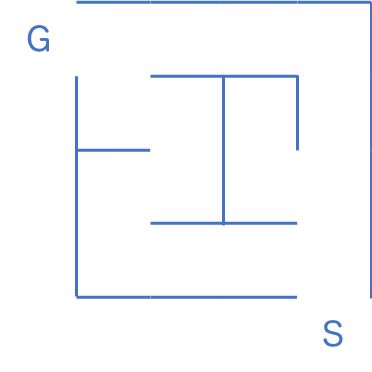
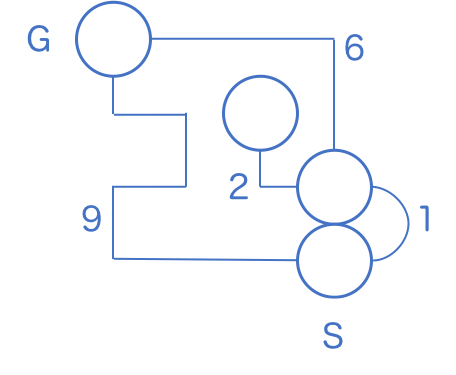
などの重要なマスだけに注目して、それ以外 (ただの一本道) を省略すると、次のように書くことができます。
一本道の脇に書かれている数字は、その道の長さです。
これはいかにも、ダイクストラ法の典型問題になっていることに気づきます。すなわち、「マスとマスの間の距離(コスト)が一定ではない状況で、最短経路を求める問題」として見ることができます。
いま、幅優先探索でこと足りる問題をわざわざダイクストラ法が必要な問題に変換できることを示しましたが、ここで重要なのは、その逆もできるということです。
すなわち、 ダイクストラ法を要求する問題も、道の長さ分のマスを勝手に補ってしまえば、幅優先探索で解ける ということです。
ダイクストラ法を幅優先探索の高速化テクだと思ってみる
幅優先探索の問題とダイクストラ法の問題を互いに変換できるなら、ダイクストラ法の問題は全部幅優先探索の問題に変換してしまって、幅優先探索だけ覚えていれば良いじゃん。というわけにはいきません。
なぜなら、たとえばコスト1兆の道がたった1本あるだけで、幅優先探索に変換するとマスがいきなり1兆個も増えてしまって、計算がめちゃめちゃ遅くなってしまうからです。
ここで、「だったら、コスト1兆の道を本当に1兆ステップかけて進むんじゃなく、1ステップで一気に1兆歩進んだことにしてしまえばいいんじゃないか?」という高速化を思いつく人がいると思います。だって、ただの一本道なんて、まじめに探索しなくても大丈夫そうに見えます。
実は、それがダイクストラ法と呼ばれるものなのでした。
「一気にたくさん進める幅優先探索」の実装
では、「一気にたくさん進める幅優先探索」(すなわちダイクストラ法) は、普通の幅優先探索にどのような変更を加えれば実装できるでしょうか。
一本道をひたすらまっすぐ進むだけならとくに考えることはないので、問題は分岐と合流です。具体的には以下の2つの「追い越し」を考慮する必要が出てきます。
探索順の追い越し (分岐時)
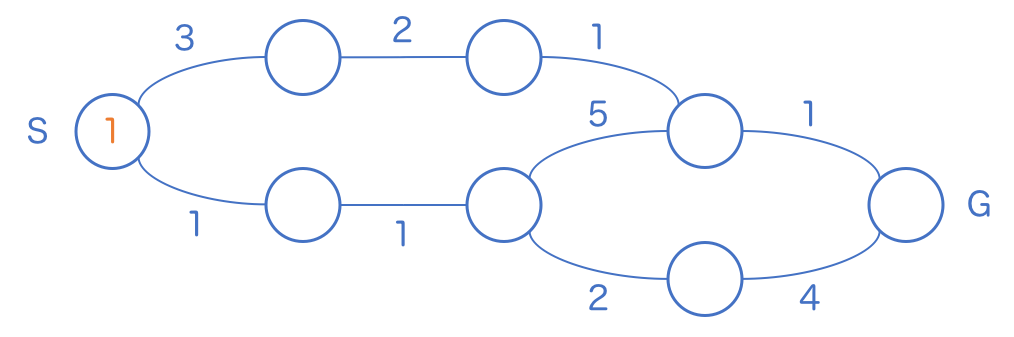
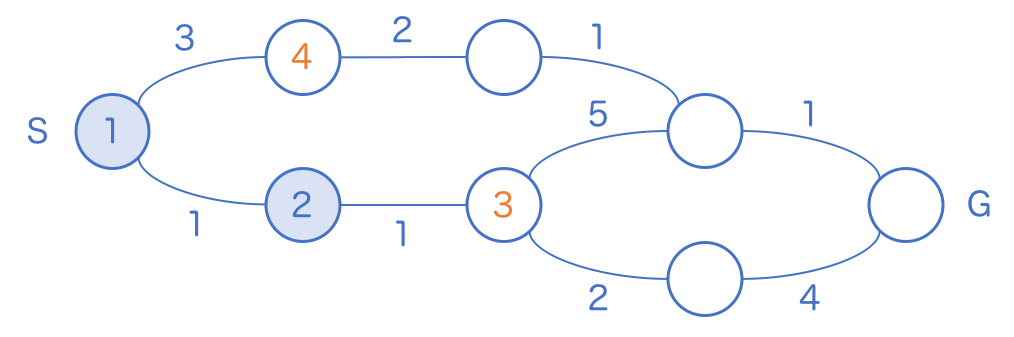
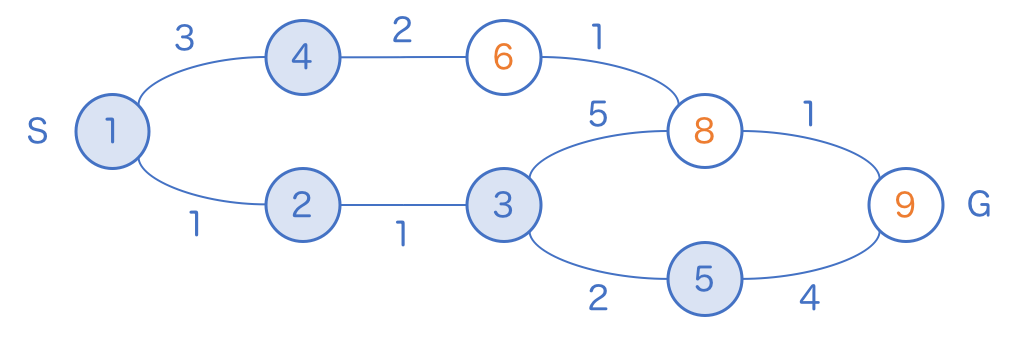
例として次のような問題を考えます。
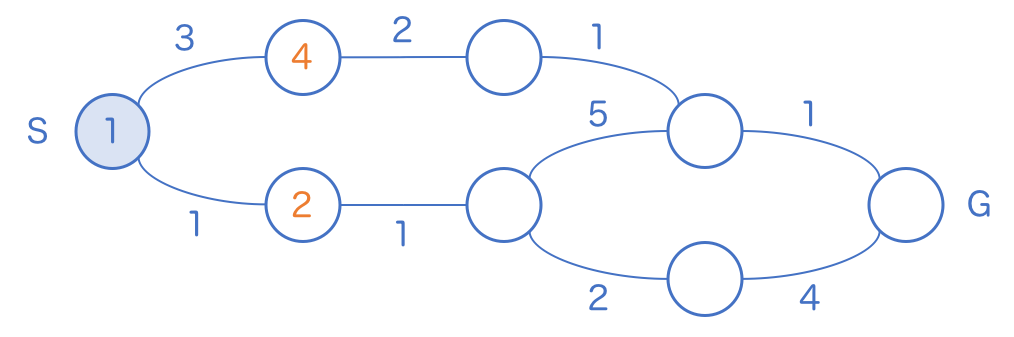
まずはスタート地点の 1 を巡回し、隣のマスに距離を書き込みます。ここまでは通常の幅優先探索と変わりません。
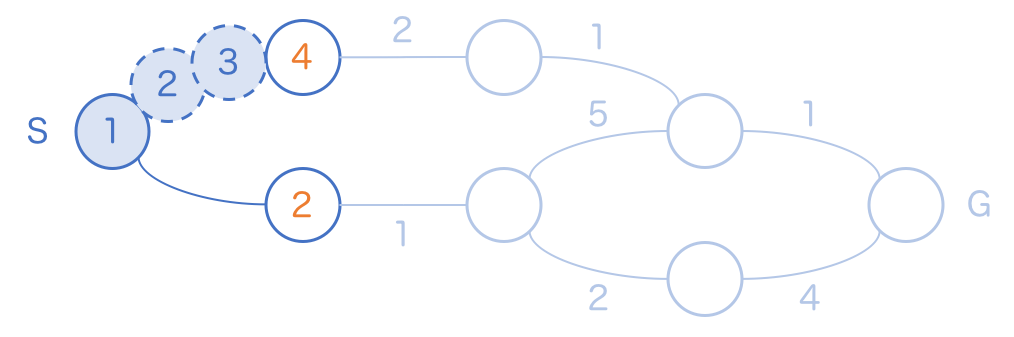
さて、通常の幅優先探索では、どちらのマスにも 2 が書き込まれ、どちらを先に巡回しても構いませんでした。しかし今回は 2, 4 とそれぞれ別の数字が書き込まれています。では次に巡回すべきマスがどちらかと考えると、直感的に 2 の方だとわかります。
なぜなら、この問題を通常の幅優先探索の問題に変換してみると、上の距離 3 の一本道には、実は2つの見えないマスが隠れていて、これらを一気にスキップした結果が 4 だと考えられるからです。他方のルートの探索がまだそこまで追いついていないなら、追いつくのを待つのが筋だと考えられます。
2 のマスを訪問すると 3 のマスが登場します。
しかしまだ 4 には追いつかないので、引き続きこのルートの探索を進めます。
ついに上ルートを追い越しました。ここにきて初めて、 4 のマスに訪問することができます。
このように、通常の幅優先探索では全てのルートを均等に探索していったのに対し、「一気に進める幅優先探索」では「他方のルートが追いつくまで待つ」といった追い越し現象が発生します。
さて、通常の幅優先探索では、探索順を効率よく決めるためにキューを使用していました。しかしキューには追い越し機能は備わっていません。そこで、追い越し機能を備えたキューである「優先度付きキュー」を使用する必要が出てきます。
while !defined cost[<ゴール>]: # ゴールのコストが判明するまで
- d = キューの先頭を取り出す()
+ d = 優先度付きキューの先頭を取り出す()
for d2 in dに隣接するマスたち:
if !defined cost[d2]: # まだコストが書いてない
- cost[d2] = cost[d] + 1
- キューの末尾に加える(d2)
+ cost[d2] = cost[d] + 距離(d から d2)
+ 優先度付きキューに加える(d2, 優先度:cost[d2])
優先度付きキューへの要素の追加・取り出しは通常 O(log n) です。ただのキューよりはやや遅いですが、しかし十分速いです。
到着順の追い越し (合流時)
分岐時だけでなく、合流時にも追い越しに気をつける必要があります。
先ほどの問題の探索をもう少し進めてみます。
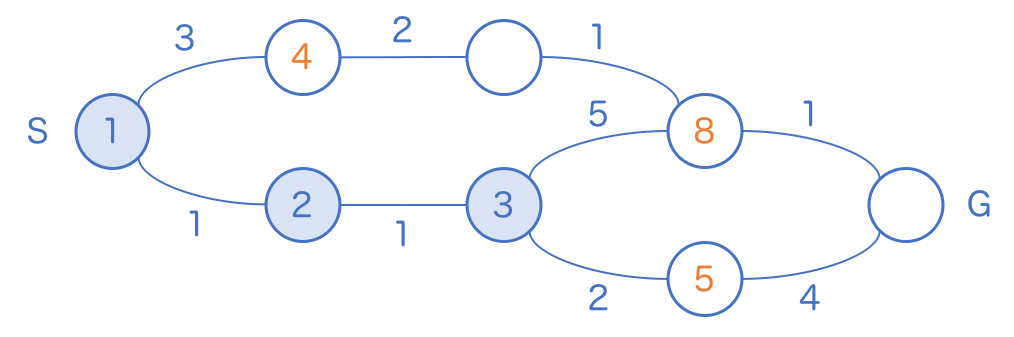
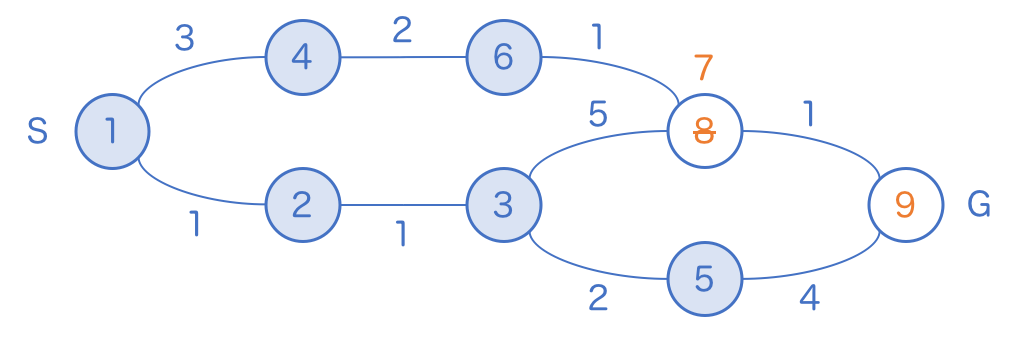
5 のマスに訪問すると、いきなりゴールのマスに 9 が書き込まれます。
通常の幅優先探索であればここで探索を打ち切ってしまっても良かったのですが、「一気に進める幅優先探索」ではまだ探索を進める必要があります。なぜでしょう。
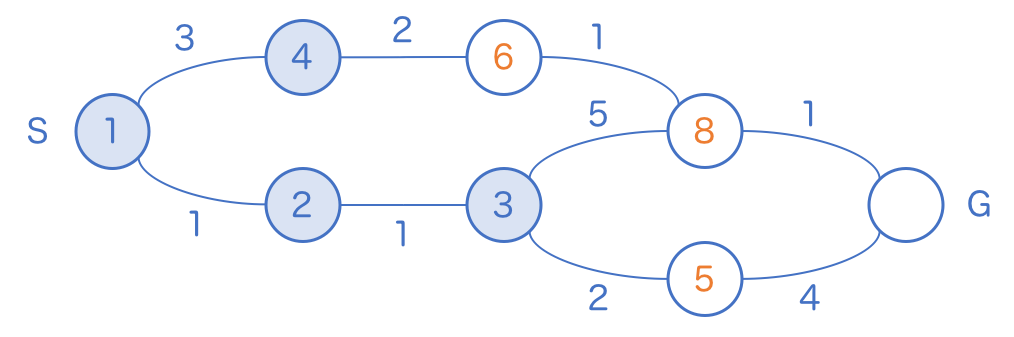
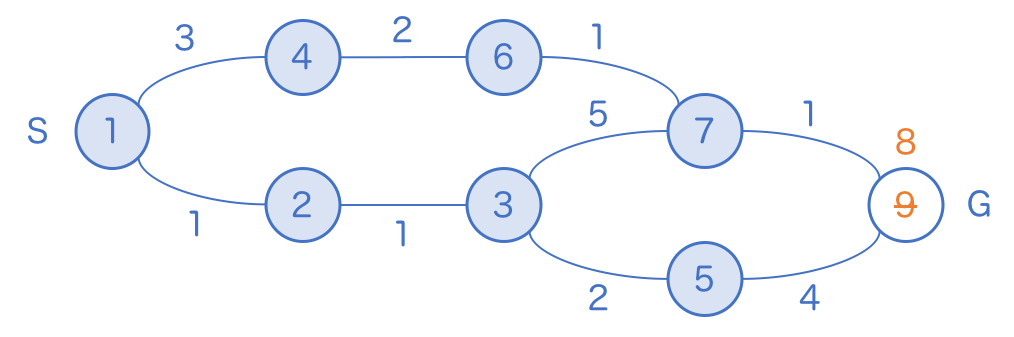
試しに 6 のマスに訪問してみると、今まで最短距離が 8 だと思われていたマスに、実は 7 歩で到達できることが発覚します。
通常の幅優先探索では、足並みを揃えてどのルートも一歩づつすすんでゆくので、当然、最短経路が一番最初に合流地点に到着します。しかし、「一気に進める幅優先探索」では長〜い道を一気に進んだ場合、一時的に最短経路を追い越して、このように先に合流地点に到着してしまうことがあります。
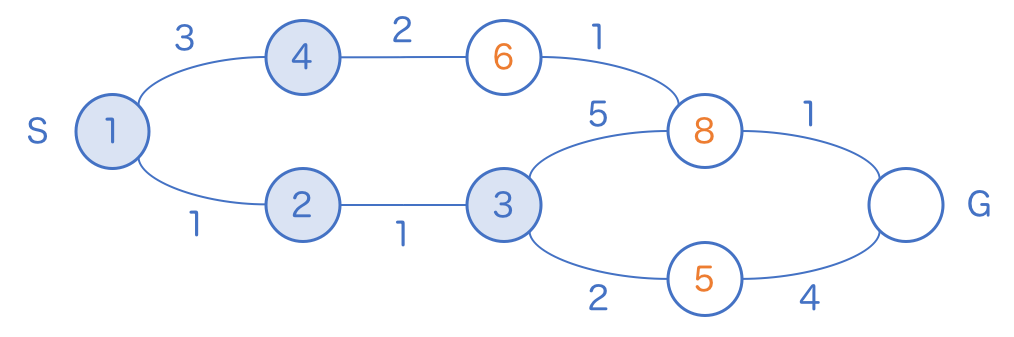
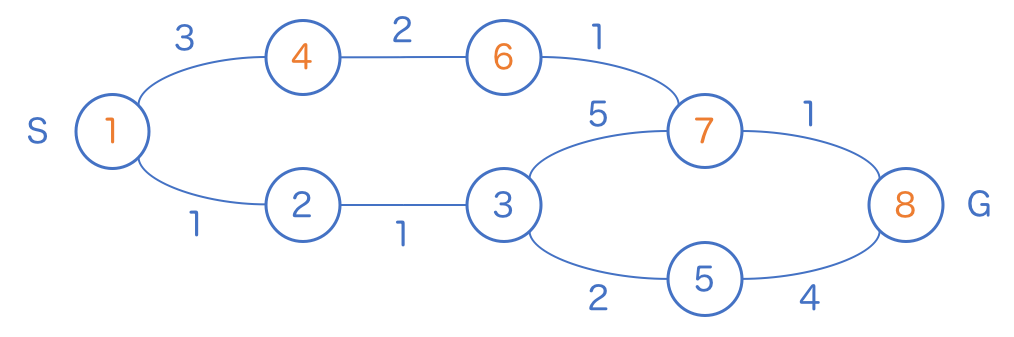
さて、このまま探索を続けてみると、実はゴールには 8 歩でたどり着くことができるとわかります。打ち切らなくて良かったです。
このように、「一気に進める幅優先探索」では、一度書き込んだ最短距離があとから更新されてしまう可能性があります。
したがってプログラムでも、その点を考慮する必要があります。
-while !defined cost[<ゴール>]: # ゴールのコストが判明するまで
+while !優先度付きキューが空(): # すべてのマスを巡回するまで
d = 優先度付きキューの先頭を取り出す()
for d2 in dに隣接するマスたち:
if !defined cost[d2]: # まだコストが書いてない
cost[d2] = cost[d] + 距離(d から d2)
優先度付きキューに加える(d2, 優先度:cost[d2])
+ elif cost[d] + 距離(d から d2) < cost[d2]:
+ # 今書いてあるコスト (cost[d2]) より速いルートが見つかった → 上書きする
+ cost[d2] = cost[d] + 距離(d から d2)
+ 優先度付きキューの並び順を更新(d2 の優先度を cost[d2] に)
これがダイクストラ法です。
おまけ1 : 経路の復元
経路の復元は幅優先探索とほぼ同じです。
ゴールからスタートして、数字が減るようにスタートまで戻ってゆきます。
ただし、減る数字の大きさと道の長さが合わない場合は、そのルートには入れません。たとえば、ゴールの 8 から 5 に進もうとすると、数字は 3 減っていますが、道の長さは 4 なので計算が合いません。このルートは最短経路ではありません。
おまけ2 : 優先度付きキューの並び順を更新 について
上の擬似コードにしれっと書いた 優先度付きキューの並び順を更新 は、実は愚直に行うと時間がかかってしまい、オーダーが悪くなってしまいます。
これを効率化するために、「優先度付きキューに同じマスを重複して並べることを認める。その代わり、同じマスは2度訪問しない」と書き変えることができます。
while !優先度付きキューが空(): # すべてのマスを巡回するまで
d = 優先度付きキューの先頭を取り出す()
+ if visited[d]: # すでに一度訪問したことがある
+ continue
+ else
+ visited[d] = true
for d2 in dに隣接するマスたち:
if !defined cost[d2]: # まだコストが書いてない
cost[d2] = cost[d] + 距離(d から d2)
優先度付きキューに加える(d2, 優先度:cost[d2])
elif cost[d] + 距離(d から d2) < cost[d2]:
# 今書いてあるコスト (cost[d2]) より速いルートが見つかった → 上書きする
cost[d2] = cost[d] + 距離(d から d2)
- 優先度付きキューの順番を更新(d2)
+ 優先度付きキューに加える(d2, 優先度:cost[d2])
優先度が更新されるときは、今わかっているルートより速いルートが見つかったときです。したがって、重複して同じマスをキューに放り込むと、後から放り込まれた方は、すでにキューに並んでいたものを追い越して、結果的に先に取り出されます。ここで、後から取り出される方、すなわちもとからキューに入っていた方を無視すれば、実質優先度を書き換えたことと同じになります。
コードの重複を消すとさらにすっきりします。
while !優先度付きキューが空(): # すべてのマスを巡回するまで
d = 優先度付きキューの先頭を取り出す()
if visited[d]: # すでに一度訪問したことがある
continue
else
visited[d] = true
for d2 in dに隣接するマスたち:
- if !defined cost[d2]: # まだコストが書いてない
- cost[d2] = cost[d] + 距離(d から d2)
- 優先度付きキューに加える(d2, 優先度:cost[d2])
- elif cost[d] + 距離(d から d2) < cost[d2]:
- # 今書いてあるコスト (cost[d2]) より速いルートが見つかった → 上書きする
+ if !defined cost[d2] || cost[d] + 距離(d から d2) < cost[d2]:
+ # まだコストが書いていないか、書いてあるコストより速いルートが見つかった
cost[d2] = cost[d] + 距離(d から d2)
優先度付きキューに加える(d2, 優先度:cost[d2])
まとめ
ダイクストラ法を幅優先探索の高速化テクとして考えてみると、個人的には覚えやすくなったというかスッキリしたので紹介してみました。
「最適性原理から明らかですね」とか言われても、感覚的にはしっくりこないところが自分はあったりしたので、あなたのしっくりの助けになれば幸いです。