今日は ABC144 の青以下の過去問を埋めました。
問題文がちょっとストーリーになっていたり、珍しく幾何があったり面白い回でした。
ABC144
ABC144 A 9x9
二つの整数が与えられるので、どちらも一桁ならその積を、そうでないなら -1 を表示する
印象
やるだけ
解法
問題文どおりに条件分岐を書いて掛け算するだけ
ABC144 B 81 [全探索]
一つの整数 N が与えられるので、それが一桁 x 一桁の掛け算に分解できるか判定する
印象
やるだけ。 B 問題にしては最低限全探索の練習になるしいい問題っぽい気がする。
解法
1 <= i <= 9 についてループ回して、 N が i で割り切れて (N % i == 0) かつ割った結果が一桁 (N / i < 10) になったら Yes と言って終わり。最後まで見つからなかったら No と言う
ABC144 C Walk on Multiplication Table [全探索]
一つの整数 N <= 10^12 が与えられるので、 a * b = N になるような a, b の組のうち a + b がもっとも小さくなるようなものを探して、その値を求める
印象
√N らへんが一番小さそう
解法
印象通り。
a + b の値を固定する (たとえば 6) と、 a, b の偏りが一番小さい時に積が一番大きくなる。
0 * 6 = 0
1 * 5 = 5
2 * 4 = 8
3 * 3 = 9
逆に言えば、掛け算を分解するときもなるべく偏りのないように (理想的には √N * √N に) 分解すると和が小さくなるはず。
i = √N からスタートして、 N を割り切れるような i が見つかるまで総当たりする。見つかったら i + N / i が答え。
ABC144 D Water Bottle [幾何]
底面が a cm の正方形で、高さが b cm ある四角い水筒がある。ここに x cm^3 の水をいれて水筒を一方向に傾けたとき、何度以上傾けると水がこぼれるか。ただし傾けるときの軸は底面の辺で、頂点ではない。
印象
arctan で一撃で求まる系っぽい
解法
だいたい印象通り。ただ実際解いてみると場合分けが必要なことに気づく (水多めパターン・少なめパターン)。
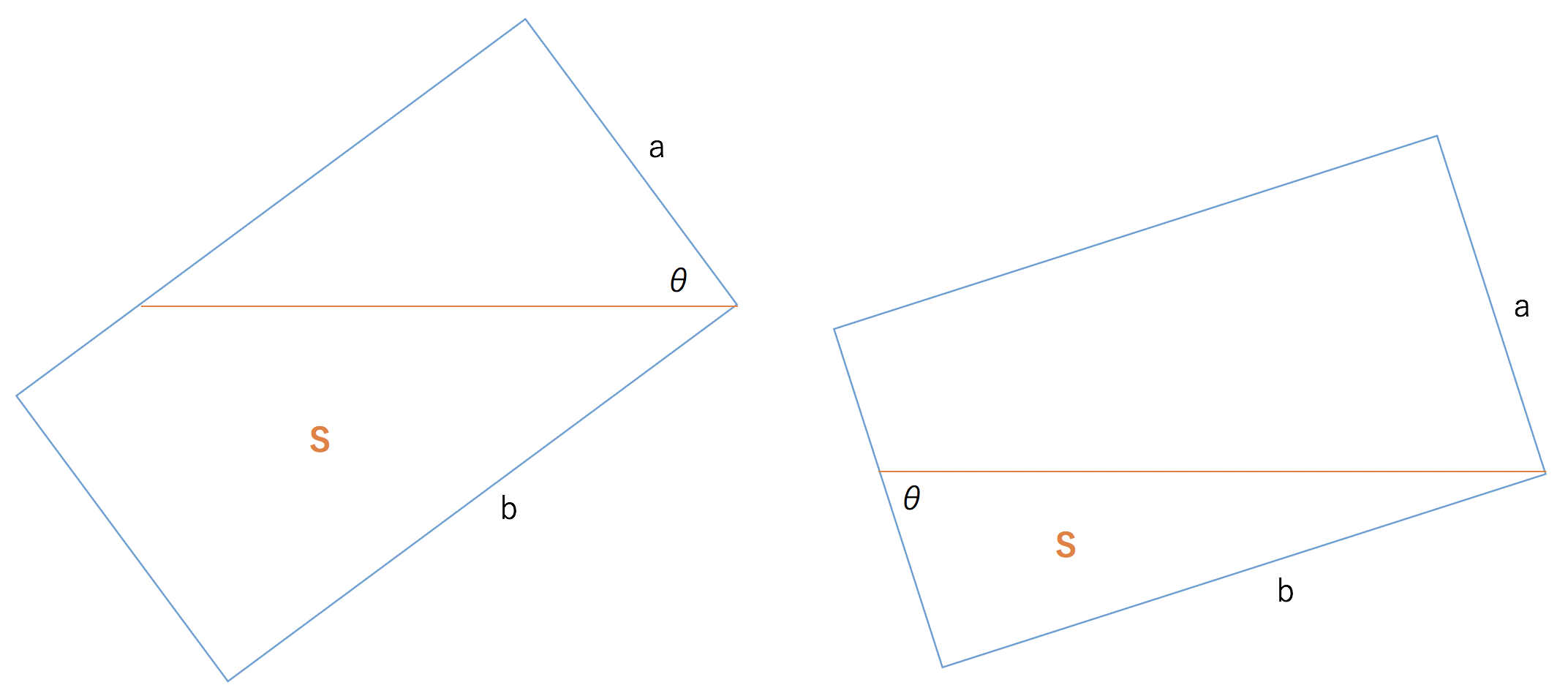
とりあえず奥行きは考える必要なさそうなので、横から見たときの面積 S = x / a で考えていく。
まずは水多めパターン(図左)を試す。
傾けても水は減らない(面積は変わらない)はずなので、オレンジの線より下の面積が S。したがって上の三角形の面積は a * b - S。一辺が a とわかっているので、もう一つの辺は三角形の面積の公式から求まる。
面積 = 底辺 x 高さ / 2
なので
高さ = 面積 x 2 / 底辺
= (a * b - S) * 2 / a
このとき、求まった高さが b より大きかったら図と矛盾するので水多めパターンではない。水少なめパターンに進む。
b 以下だった場合、水多めパターンで合っているので、そのまま arctan で角度を求めて終了。
水少なめパターン(図右)では、今度はオレンジより下の面積 S のエリアが三角形になる。こちらに対して同じように面積の公式を使うと
高さ = S * 2 / b
同様に arctan で角度を求めれば答え。
ABC144 E Gluttony [二分探索]
N <= 2 * 10^5 人のメンバーがいて、それぞれの人にお腹の弱さ A[i] <= 10^6 が決められている。 K <= 10^18 の予算が用意されていて、 1 使うごとにメンバー 1 人のお腹の弱さを 1 改善することができる (0 未満にはならない)。
一方、料理も N 種類用意されていて、それぞれの料理に消化の悪さ F[i] <= 10^6 が決められている。お腹の弱さが a の人に消化の悪さ f の料理を食べさせると、食べきるのに a * f の時間がかかる。
メンバーたちを適切に鍛えて、料理を適切に割り当てたとき、すべて食べきるのにかかる時間(一番遅い人が食べ終わる時間)はいくらか。ただし一人のメンバーには一つの料理しか割り当てられない。
印象
一番お腹の弱いメンバーに一番消化のいいものを食べさせればいいので、料理の割り当て方は決め打ちで良さそう。
あとはどう鍛えるかが問題。
K がかなりでかいので、一番遅い人を検索しては 1 ずつ鍛える、というのを延々繰り返していても埒が明かない。
A[i] * f[i] の配列を作ってソートして、ガッと大きい方から「ここからここまで鍛える」みたいにやれるのかな…、うーん。
解法
二分探索で一撃 (log N 撃) だった。「ほげほげできる最小の x を求めよ」を見たらとりあえずにぶたんを疑ってみるのが正解な気がする。これは思いつきたかったな…。
「予算 K で t 分以内に食べきれるか」は判定可能。各メンバーについて、必要な予算を次のように計算できる:
-
F[i]のものをt分で食べきるのに必要なお腹のコンディションはt / F[i] - もし
t / F[i] > A[i]なら、これ以上鍛えなくてもこのメンバーは食べきれるので予算0 - そうでない場合、このメンバーは足りない分
A[i] - t / F[i]だけ鍛える必要がある
全員の予算の合計が K を超えてしまったら、 t 分以内には食べきれない。
あとは絶対食べきれない -1 分と絶対食べきれる 10^12 + 1 分のちょうど真ん中からスタートして、範囲を半々に絞り込んでいけば境目が見つかる。総当たりでは間に合わない。