Bayesian Optimization of Function Networks(BOFN)の可視化

• 基礎的なベイズ的最適化の概念については説明していません
• Sample Average Approximationは扱いません
• 記事に誤りがある可能性があります。指摘していただけると幸いです。

概要

2021年のNeurIPSで発表されたBayesian Optimization of Function Networks(BOFN)のベイズ的最適化のアルゴリズムを可視化して説明します。

通常ベイズ的最適化を行うときの問題設定は入力と出力以外観測することができないブラックボックスな問題として扱われます。しかし、現実の問題を最適化するときには出力以外のさまざまな情報が得られることがあります。そこで、最適化するシステム入出力以外を利用し、より効率的な最適化を目指すグレイボックス最適化が近年注目されており、BOFNもその一種です。

アルゴリズムの説明

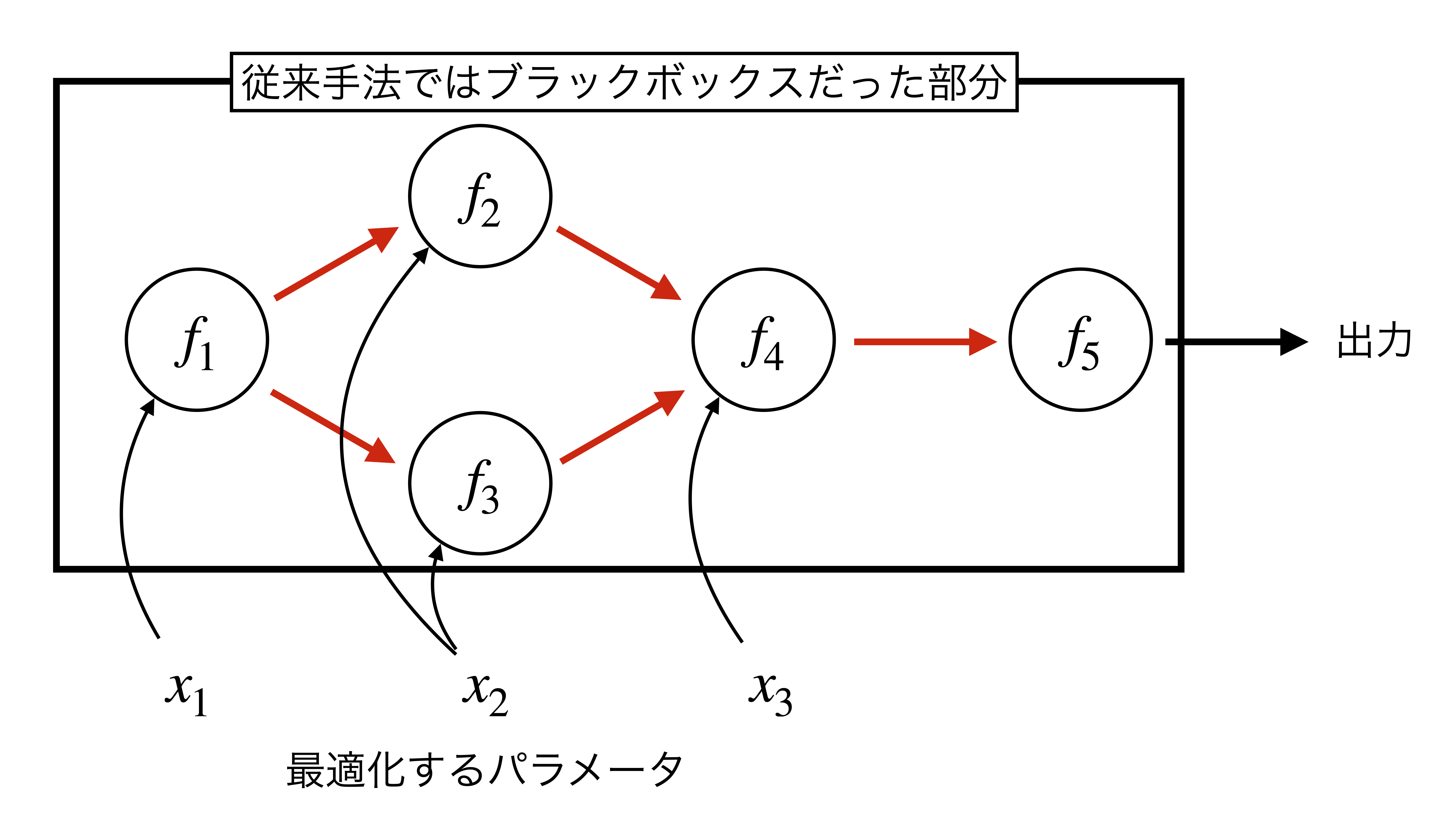
問題設定

有向非巡回グラフを考え、ノード $k$における関数を $f_k$とします。
それぞれのノードは、最適化するパラメータ $\textbf{x}$、親ノードの出力を入力として受け取ることができます。

従来のブラックボックス最適化では、これらのグラフ構造を無視します。したがって、黒色の矢印で示されるような最適化するシステムへの入出力のみを観測することができます。

一方、グレイボックス最適化では従来のブラックボックス最適化で無視していた情報を加味することで効率的に最適化を行います。今回紹介するBOFNはグラフ構造を認識しており、それぞれのノードの出力(赤色の矢印)も併せて観測することができます。

確率モデル

従来の手法を上記の問題設定にそのまま適用することは難しいため工夫が必要となります。そこで以下のような方針をもとに獲得関数の算出を行います。

1. $f_1$、 $\ldots$、 $f_K$のそれぞれについてガウス過程回帰を行う
2. ガウス過程回帰の結果から出力のサンプルを得ることは可能！！
3. モンテカルロ法に基づいて獲得関数を算出

まず方針の1番ですが、これは既存の手法をそのまま適用することで実現できます。

例えば、下図のように $x_1$を入力として関数 $f_1$、 $f_2$ を経て $g$という出力が得られる問題について考えます。グレイボックスな問題設定では $f_1$のノードの出力でもある $h_1$を観測することが可能です。

したがって入力を $x_1$、 出力を $h_1$とすれば $f_1$のガウス過程回帰を、入力を $h_1$、 出力を $h_2$とすれば $f_2$のガウス過程回帰を行うことができます。¹

続いて方針の2番ですが、こちらがこの論文の最重要な部分になっていると思います。

上の図のように$f_1$、 $f_2$のそれぞれについてガウス過程回帰を行うことができました。続いて$x_1$を入力としたときの出力 $g$に関する予測を行って行きたいです。

しかし、 $x_1$を入力としたときの出力 $g$の分布はガウス分布にならないため閉形式で分布を求めることはできません。そこで、 $x_1$を入力としたときの出力 $g$のサンプルを得ることは可能であるということを説明し、次のモンテカルロ法に基づく獲得関数の算出に話をつなげていきます。

下図は先ほど得たガウス過程回帰の結果から $x_1$における $g$の結果をサンプリングしている様子を示しています。ガウス過程回帰では、ある$x_1$において$h_1$は以下のようにガウス分布に従った形で予測されます。

$$ h_1(x_1) \sim \mathcal{N}\left( \mu(x_1)、 \sigma(x_1)^2\right)$$

ただし$\mu$と$\sigma^2$はある$x_1$における$h_1$の平均と分散を示しています。

上のガウス分布にしたがう $h_1$の値を乱数などに基づいてサンプリングしてくることができます。同様に、ある$h_1$において$h_2$もガウス分布に従った形で予測されるため、先ほどサンプリングしてきた $h_1$における $h_2$の値をサンプリングしてくることも可能です。

これはある$x_1$における $g$の予測分布からサンプルを取ってくることができたことを意味します。乱数に従いこのサンプルを無数に取り続ければ下図の一番右のように $g$の予測分布のようなものを得ることもできます。

最後に方針の3番について説明します。

$g$の事後分布に基づくサンプリングができることを示しました。

ベイズ的最適化の獲得関数としてよく用いられるものとしてExpected Improvement(EI)というものがあります。EIは事後分布$g(x)$から、これまでに得た最大の値$g_n^*$よりも大きくなる確率を求めます。

$$ \text{EI-FN} = \mathbb{E} \left[ {g(x) - g_n^*}\right] \tag{1}$$

今回の手法では事後分布g(x)を閉形式で求めることできませんが事後分布からサンプルを取ることは可能であることを方針2で示しました。

モンテカルロ法に基づくと、ある関数$f(x)$が確率分布p(x)のもとで得られるときその期待値$\mathbb{E} [f] = \int p(x)f(x) dx$を、確率分布にしたがって得られる有限個の$N$以下の式により近似できます。(パターン認識と機械学習 上 p.19より)

$$ \mathbb{E}[f] \simeq \frac{1}{N}\sum_{n=1}^{N} f(x_n) $$

これを式(1)に適用することで以下のように獲得関数の近似式を得ることができます。

$$ \text{EI-FN} \approx \frac{1}{M} \sum_{n=1}^{N} \left( \hat{g}(x)_{(n)} - g_n^{*}\right)^{+}$$

補足

• 論文では獲得関数の最大化にSample Average Approximationという手法を用いていますが、とりあえず獲得関数を求めるところまでが手法の重要なところかなと思ったので省略しました。
• 可視化のためのコード(https://github.com/zinutag/visualization_bofn)

1. $g$はグラフの最終出力、 $h_k$はノード $k$の出力という使い分けです。したがって今回の問題設定では $h_2$ = $g$となります。 ↩