LoginSignup
2
1

More than 3 years have passed since last update.

@zhidao(Zhidao)

ポインタを用いた（配列を使わない）2分ヒープの実装

Last updated at Posted at 2020-11-13

前書き

2分ヒープ（バイナリヒープ）は、2分木を用いた効率的なデータ格納方法の一つですが、実装例として巷で紹介されているのは配列を用いたものばかりのようです。もちろんそれは、概念通りに2分木で実装するよりも利点が多い（例えばデータへのアクセスの計算量がO(1)、データの入れ替え操作が単純である等）からなのですが、格納する最大データ数が事前に全く分からない場合にはやはり配列は不便です。

ポインタを用いた2分ヒープの実装に関して、例えば次のページが見つかりました。

本記事では、上記で紹介されているいずれの例よりも少しコンパクトな実装を示します。使用言語はC言語、テスト環境はUbuntu 18.04、GCC 7.5.0ですが、C89に則っているのでほとんどの環境で動くはずです。

コード全体

最初に、テスト用main()関数も含めたコード全体を示します。後ほど各部について説明します。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

typedef struct __heap_t{
  struct __heap_t *child[2];
  unsigned int size;
  int data;
} Heap;

unsigned char HeapIsEmpty(Heap *tree)
{
  return tree->size == 0;
}

Heap *HeapInit(Heap *node)
{
  node->child[0] = node->child[1] = NULL;
  node->size = 0;
  return node;
}

void HeapNodeDestroy(Heap *node)
{
  if( node->child[0] )
    HeapNodeDestroy( node->child[0] );
  if( node->child[1] )
    HeapNodeDestroy( node->child[1] );
  free( node );
}

void HeapDestroy(Heap *tree)
{
  if( tree->child[0] )
    HeapNodeDestroy( tree->child[0] );
  HeapInit( tree );
}

Heap *HeapNodeAlloc(int val)
{
  Heap *node;

  if( !( node = malloc( sizeof(Heap) ) ) ){
    perror( NULL );
    return NULL;
  }
  HeapInit( node );
  memcpy( &node->data, &val, sizeof(int) );
  return node;
}

void HeapNodeSwap(Heap *parent, int id, Heap *node, int cid)
{
  Heap *tmp;

  parent->child[id] = node->child[cid];
  node->child[cid] = node->child[cid]->child[cid];
  parent->child[id]->child[cid] = node;
  tmp = node->child[1-cid];
  node->child[1-cid] = parent->child[id]->child[1-cid];
  parent->child[id]->child[1-cid] = tmp;
}

unsigned int HeapMaskInit(Heap *tree)
{
  unsigned int mask;

  mask = 1 << ( sizeof(int)*8 - 2 );
  while( !( mask & tree->size ) ) mask >>= 1;
  return mask >> 1;
}

Heap *HeapNodeAdd(Heap *parent, int id, Heap *node, Heap *node_new, unsigned int mask, unsigned int size, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  unsigned int cid;

  cid = mask & size ? 1 : 0;
  if( mask == 1 )
    node->child[cid] = node_new;
  else
    HeapNodeAdd( node, cid, node->child[cid], node_new, mask >> 1, size, cmp, util );
  if( !cmp( node, node->child[cid], util ) )
    HeapNodeSwap( parent, id, node, cid );
  return node_new;
}

Heap *HeapAdd(Heap *tree, int val, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  Heap *np_new;
  unsigned int mask;

  if( !( np_new = HeapNodeAlloc( val ) ) ) return NULL;
  if( ++tree->size == 1 ){
    tree->child[0] = np_new;
    return tree->child[0];
  }
  mask = HeapMaskInit( tree );
  return HeapNodeAdd( tree, 0, tree->child[0], np_new, mask, tree->size, cmp, util );
}

void HeapDown(Heap *parent, int id, Heap *node, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  unsigned int cid;

  if( !node->child[0] ) return;
  cid = !node->child[1] ? 0 : ( cmp( node->child[0], node->child[1], util ) ? 0 : 1 );
  if( !cmp( node, node->child[cid], util ) ){
    HeapNodeSwap( parent, id, node, cid );
    HeapDown( parent->child[id], cid, node, cmp, util );
  }
}

Heap *HeapDelete(Heap *tree, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  Heap *ret, *np;
  unsigned int mask, cid;

  mask = HeapMaskInit( tree );
  for( np=tree->child[0]; np; mask>>=1, np=np->child[cid] ){
    cid = mask & tree->size ? 1 : 0;
    if( mask == 1 ) break;
  }
  ret = tree->child[0];
  if( !np ){
    tree->child[0] = NULL;
  } else if( ( tree->child[0] = np->child[cid] ) ){
    np->child[cid] = NULL;
    tree->child[0]->child[0] = ret->child[0];
    tree->child[0]->child[1] = ret->child[1];
    HeapDown( tree, 0, tree->child[0], cmp, util );
  }
  ret->child[0] = ret->child[1] = NULL;
  tree->size--;
  return ret;
}

void HeapNodePrint(Heap *node, int indent)
{
  printf( "%*d\n", indent, node->data );
  if( node->child[0] ) HeapNodePrint( node->child[0], indent+2 );
  if( node->child[1] ) HeapNodePrint( node->child[1], indent+2 );
}

void HeapPrint(Heap *tree)
{
  if( !HeapIsEmpty( tree ) )
    HeapNodePrint( tree->child[0], 0 );
}

int HeapComp(Heap *node1, Heap *node2, void *util)
{
  return node1->data <= node2->data ? 1 : 0;
}

#define N 20

int main(int argc, char *argv[])
{
  Heap tree, *node;
  int i;

  srand( time( NULL ) );
  HeapInit( &tree );
  for( i=0; i<N; i++ )
    HeapAdd( &tree, rand() % 11, HeapComp, NULL );
  HeapPrint( &tree );

  printf( "delete\n" );
  while( !HeapIsEmpty( &tree ) ){
    HeapNodePrint( ( node = HeapDelete( &tree, HeapComp, NULL ) ), 0 );
    free( node );
  }
  HeapDestroy( &tree );
  return 0;
}

% gcc test.c だけでコンパイルできるはずです。string.hとtime.hをインクルードしているのは、それぞれmemcpy()、time()を用いるためですが、memcpy()は汎用性を意識したデータコピー、time()はテスト用の乱数シードに用いているもので、実装に応じて除外して構いません。

データ構造（2分木）の定義と初期化・破棄処理

2分木のノードは次のように定義します。

typedef struct __heap_t{
  struct __heap_t *child[2];
  unsigned int size;
  int data;
} Heap;

child[]は二つの子ノードへのポインタです。ヒープでは「親子ノードの入れ替え」という操作が必要になるので、親ノードへのポインタも持っている方が良いように思うかも知れませんが、それは必須ではなく、むしろそれによってポインタつなぎ変え操作が煩雑になるので避けました。
sizeは全てのノード数を格納しておくもので、本記事の実装だと根ノードだけが持っていれば良いです。そう考えると少し無駄なようにも感じますが、部分木のヒープ化等の処理（上記コードでは実装していません）を行うのに必要になってくるはずなので入れておきました。気になる方は、ノードとは別に木（根ノードへのポインタと全てのノード数を持つ）を定義すれば良いと思います。この記事の実装では、最初に定義したノードはダミーで、そのchild[0]を根ノードとしています。
dataはデータ本体で、適当にint型としています。

次は空木かどうかの判定、ノードの初期化、ノードの破棄、木全体の破棄を行う関数で、いずれも特に解説は必要ないと思います。

unsigned char HeapIsEmpty(Heap *tree)
{
  return tree->size == 0;
}

Heap *HeapInit(Heap *node)
{
  node->child[0] = node->child[1] = NULL;
  node->size = 0;
  return node;
}

void HeapNodeDestroy(Heap *node)
{
  if( node->child[0] )
    HeapNodeDestroy( node->child[0] );
  if( node->child[1] )
    HeapNodeDestroy( node->child[1] );
  free( node );
}

void HeapDestroy(Heap *tree)
{
  if( tree->child[0] )
    HeapNodeDestroy( tree->child[0] );
  HeapInit( tree );
}

次の関数はノードを新規作成するものです。汎用性を少し意識してデータコピーにmemcpyを用いていますが、この例ではintなので単なる代入でももちろん構いません。

Heap *HeapNodeAlloc(int val)
{
  Heap *node;

  if( !( node = malloc( sizeof(Heap) ) ) ){
    perror( NULL );
    return NULL;
  }
  HeapInit( node );
  memcpy( &node->data, &val, sizeof(int) );
  return node;
}

親子ノードの入れ替え

次の関数はnodeとその子node->child[cid]を入れ替えるものです。

void HeapNodeSwap(Heap *parent, int id, Heap *node, int cid)
{
  Heap *tmp;

  parent->child[id] = node->child[cid];
  node->child[cid] = node->child[cid]->child[cid];
  parent->child[id]->child[cid] = node;
  tmp = node->child[1-cid];
  node->child[1-cid] = parent->child[id]->child[1-cid];
  parent->child[id]->child[1-cid] = tmp;
}

先述した通り、ノード自身が親を知らないので、親子ノードの入れ替えには「親ノードの親」の情報が必要になります。parent->child[id]がnodeであること、node->child[cid]がNULLでないことを前提にしています（これらの前提が崩れたらこの関数は破綻します）。
↓こんな流れで入れ替えています。
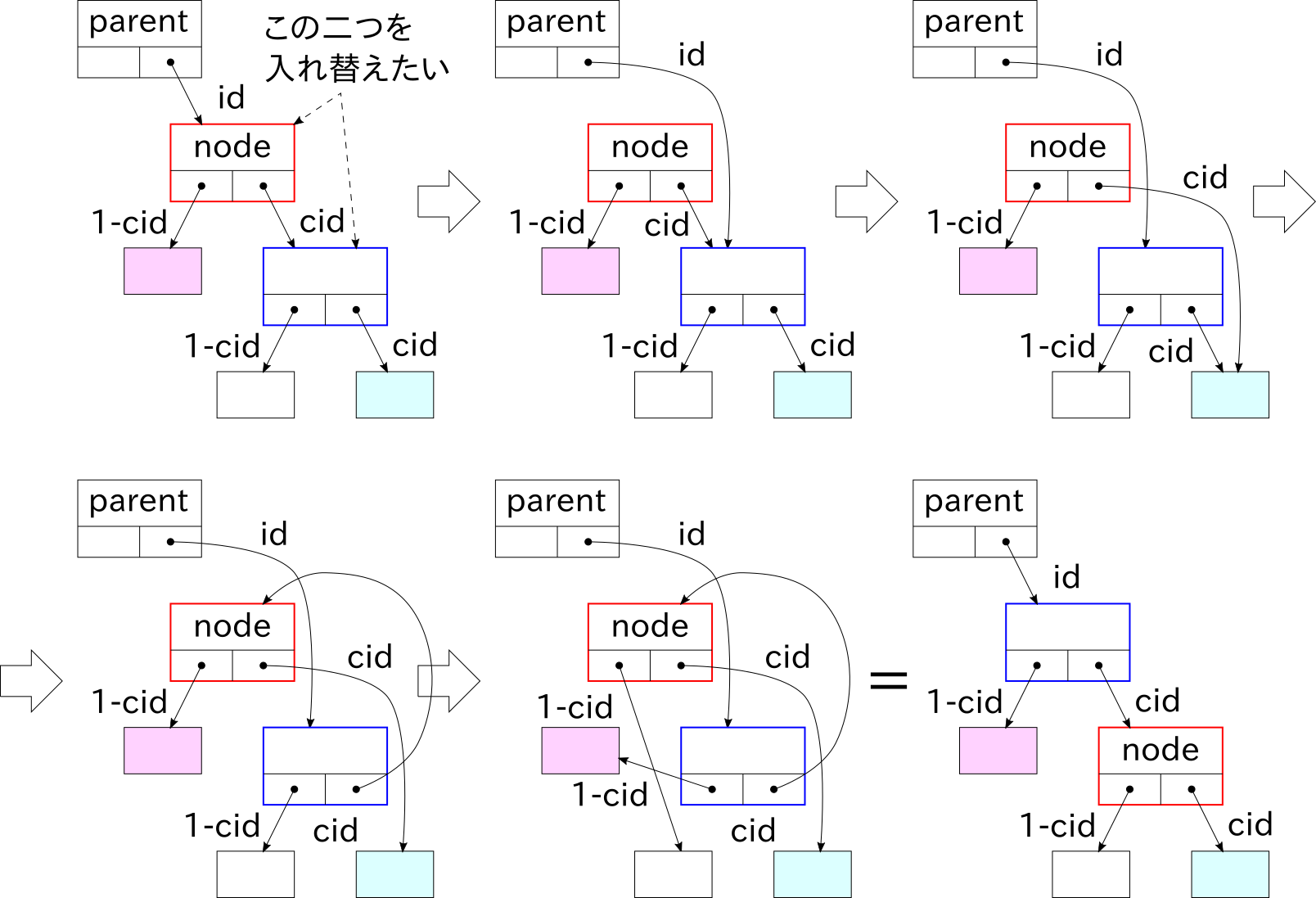
bitmap.png
2分木なので、node->child[cid]でない方の子ノードはnode->child[1-cid]であることを利用しています。

ノード挿入

試しに根ノードから2番目～10番目のノードに辿り着くパスを2進数で表してみます。例えば001だったら、root->child[0]->child[0]->child[1]であることを意味しています。

ノード番号 (2進数表記) パス
2 10 0
3 11 1
4 100 00
5 101 01
6 110 10
7 111 11
8 1000 000
9 1001 001
10 1010 010

以上から類推できるように、1が現れる最大ビットは辿る階層の数、それ以降はパスにそれぞれ対応しています。このことに基づいてノード挿入操作を行っているのが次の関数群です。

unsigned int HeapMaskInit(Heap *tree)
{
  unsigned int mask;

  mask = 1 << ( sizeof(int)*8 - 2 );
  while( !( mask & tree->size ) ) mask >>= 1;
  return mask >> 1;
}

Heap *HeapNodeAdd(Heap *parent, int id, Heap *node, Heap *node_new, unsigned int mask, unsigned int size, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  unsigned int cid;

  cid = mask & size ? 1 : 0;
  if( mask == 1 )
    node->child[cid] = node_new;
  else
    HeapNodeAdd( node, cid, node->child[cid], node_new, mask >> 1, size, cmp, util );
  if( !cmp( node, node->child[cid], util ) )
    HeapNodeSwap( parent, id, node, cid );
  return node_new;
}

Heap *HeapAdd(Heap *tree, int val, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  Heap *np_new;
  unsigned int mask;

  if( !( np_new = HeapNodeAlloc( val ) ) ) return NULL;
  if( ++tree->size == 1 ){
    tree->child[0] = np_new;
    return tree->child[0];
  }
  mask = HeapMaskInit( tree );
  return HeapNodeAdd( tree, 0, tree->child[0], np_new, mask, tree->size, cmp, util );
}

HeapMaskInit()は1である最大ビットを見つける関数です。sizeをint型で定義しているので、最初にsizeof(int)*8-2としています（MSBが正負符号に対応するため）。unsigned int型（またはsize_t型）で定義するならばsizeof(unsigned int)-1（またはsizeof(size_t)-1）とすれば良いです。
ヒープの挿入は、まず末端に新しいノードを追加し、親ノードの要素が自分よりも小さいならば親子交換する、という操作を遡りながら行うことでなされます。ノード自身が親ノードを知らないので、HeapNodeAdd()関数で再帰を使ってこれを実装しています。ユーザはHeapAdd()だけ呼べばOKです。
汎用性を意識して、比較関数cmp()を引数で与えるようにしています。utilはcmp()に与えるユーザ定義引数です。

配列を使えばノードへのアクセス計算量はO(1)ですが、上記の方法ではO(logN)となってしまいます。末端ノードのポインタを保持すればO(1)になりますが、ノードが増えたときに末端を隣の木に移す操作が結局O(logN)になるので、あまり変わりません。ポインタを用いる実装ではこれは仕方ないようです。

ノード削除

ヒープでは、常に根ノードから削除します。そして末端ノードを暫定的に根ノードにすげ替え、その要素よりも小さい要素を持つ子ノードがあるならばそれと（どちらの子ノードの要素も小さかったら、より小さい要素を持つ方と）親子交換する、という操作を順次行うことで、全体構造を維持します。これを行うのが次の関数群です。

void HeapDown(Heap *parent, int id, Heap *node, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  unsigned int cid;

  if( !node->child[0] ) return;
  cid = !node->child[1] ? 0 : ( cmp( node->child[0], node->child[1], util ) ? 0 : 1 );
  if( !cmp( node, node->child[cid], util ) ){
    HeapNodeSwap( parent, id, node, cid );
    HeapDown( parent->child[id], cid, node, cmp, util );
  }
}

Heap *HeapDelete(Heap *tree, int (* cmp)(Heap*,Heap*,void*), void *util)
{
  Heap *ret, *np;
  unsigned int mask, cid;

  mask = HeapMaskInit( tree );
  for( np=tree->child[0]; np; mask>>=1, np=np->child[cid] ){
    cid = mask & tree->size ? 1 : 0;
    if( mask == 1 ) break;
  }
  ret = tree->child[0];
  if( !np ){
    tree->child[0] = NULL;
  } else if( ( tree->child[0] = np->child[cid] ) ){
    np->child[cid] = NULL;
    tree->child[0]->child[0] = ret->child[0];
    tree->child[0]->child[1] = ret->child[1];
    HeapDown( tree, 0, tree->child[0], cmp, util );
  }
  ret->child[0] = ret->child[1] = NULL;
  tree->size--;
  return ret;
}

HeapDelete()の最初のforループで、末端ノードを見つけます。考え方はノード挿入の方法と同じです。根ノードをretとして、それと末端ノードとすげ替える操作をしています（ノードを一つしか持たない木の場合は末端ノードはNULLになるので、例外処理します）。子ノードの要素が新たな根ノードの要素よりも小さい場合の入れ替え操作を再帰的に行うのがHeapDown()関数です。こちらの理解は難しくないと思います。

テスト結果

最初に示した全体コードをコンパイル、実行した結果は次の通りです。

0
 1
   2
     5
      10
       9
     2
       6
       8
   1
     5
       9
     5
 4
   7
     9
     7
   6
     9
     9
delete
0
1
1
2
2
4
5
5
5
6
6
7
7
8
9
9
9
9
9
10

2分木の表示が手抜きなのはご勘弁下さい。データは乱数的に生成しているので実行ごとに異なりますが、空になるまでノードを取り出し値を列記していった結果、値が昇順にソート（ヒープソート）されることが分かります。

2
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
1