何の話?
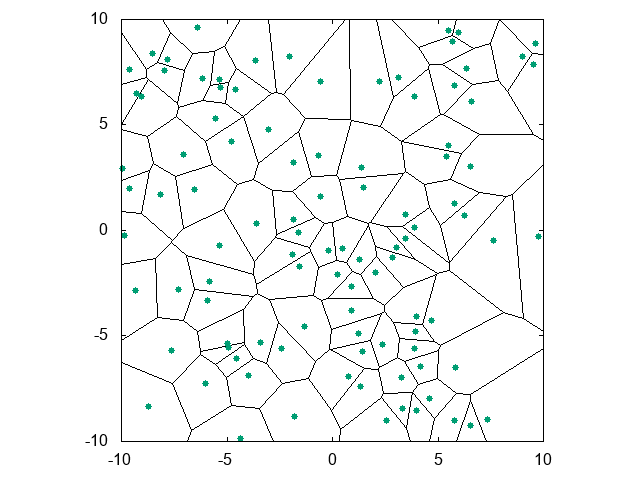
Voronoi線図が何かという説明は省きます。上のような図を見て、この図の外側はどうなってるのかな?という疑問を持った人向けの記事です。それは恐らく、
- 自分でVoronoi線図を描くプログラムを実装しよう
- 図を描くだけでなく、そのデータ構造を使って~しよう
という、私と同じ動機を持った方々だと思いますので、そのような方々のお役に立てれば幸いです。
Voronoi線図を描く方法
Voronoi線図を描く方法は幾つも知られていますが、個人的にはDelaunay三角形分割を先にするのが一番良いと考えます。たとえば上図の同じ点群に対して、次のようなDelaunay線図が描けます。
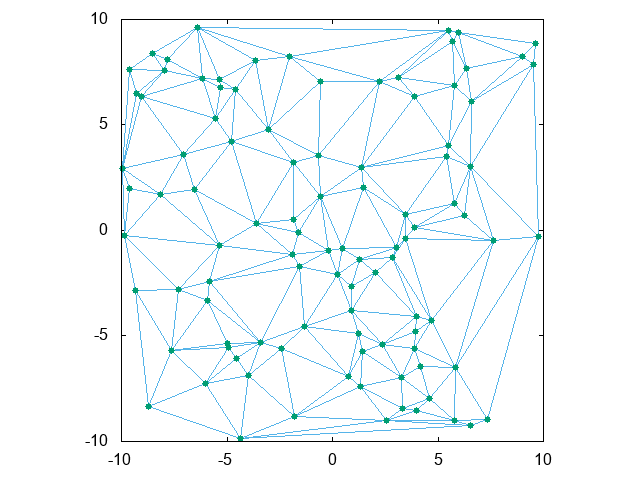
良く知られているように、Delaunay線図とVoronoi線図は双対関係にあります。上の二つの図を次のように重ねれば、各Voronoi節点が各三角形の外心になっている様子がお分かり頂けると思います。
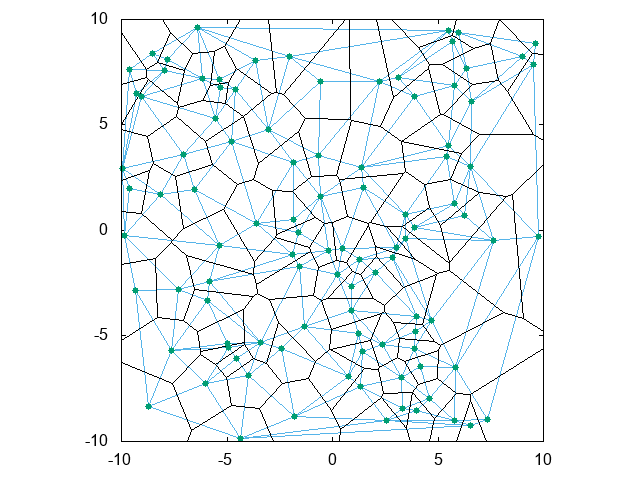
したがって全ての三角形について、その外心と、隣接する三つの三角形の外心とをそれぞれ線分で結んでやれば(そして線分の重複描画を許容するならば)、Voronoi線図を描くことができます。ただし図を描くだけでなく、データ構造としてVoronoi細胞(各々の点を取り囲む多角形)を作りたいならば、もうひと手間必要です。
Delaunay線図の構成要素は三角形だけで、しかも与えられた点群の凸包内に全て収まるので、データの持ち方で悩むことはあまりありません。一方Voronoi線図の方は、外縁にある点群に対するVoronoi細胞が非有界領域になります。つまり理論上、無限遠点に延びる稜線が現れます。外縁でない点のVoronoi細胞と違ってループが閉じませんし、そもそも無限遠点はプログラムでは表せません。これどうするの?というのが本記事の関心事項です。
Voronoi線図の外縁=Delaunay三角形分割の外縁の外心
Delaunay三角形分割をする際には、「与えられた点群を内包する三角形」を最初に作り、それを用いて三角形分割した後、最初に作った大きな三角形の頂点を含む三角形群(外縁三角形群)を削除する、という手順をとります。
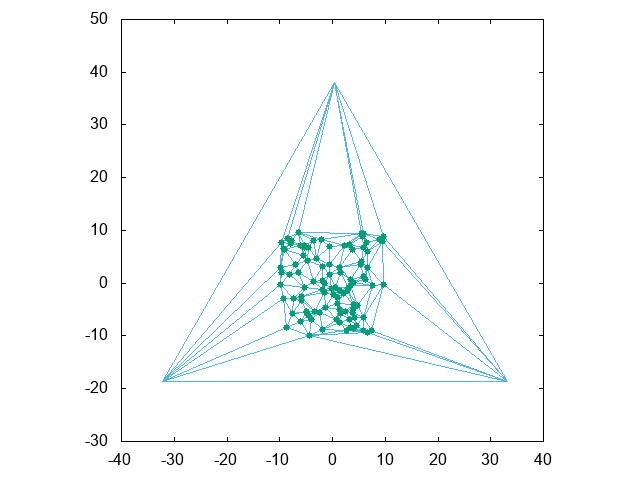
上の図では最後の手順を省き、外縁三角形群を残してあります。そしてその三角形群も含めれば、全ての三角形の外心によって「閉じた」Voronoi細胞のみを構成することができます。実際に描いたものが次の図です。
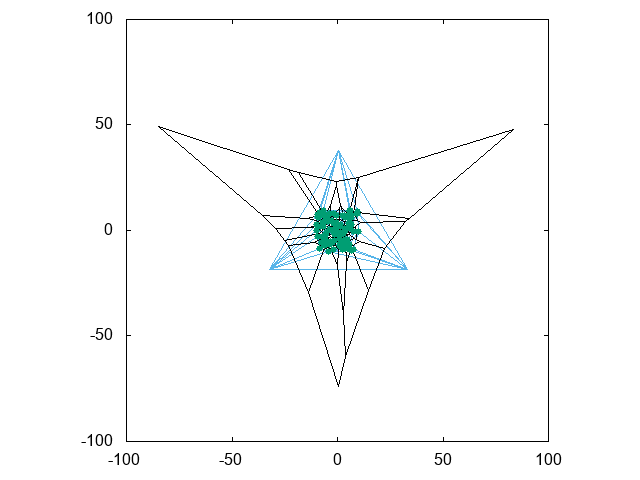
Voronoi線図を描いたときの関心領域は点群近辺に集まっているので、上図のVoronoi細胞の外縁は実用上十分遠方にあると考えて差し支えありません。
なお、上記に用いた計算はZeoに実装されています。
おまけ:Delaunay三角形分割とVoronoi線図のアルゴリズム実装について
繰り返しになりますが、Voronoi線図を描く一番良い方法は、Delaunay三角形分割を先にすることだと私は考えます。「良い」というのは、アルゴリズムのシンプルさとロバストさの二つの観点からです。計算量の観点からは逐次添加法で直接Voronoi線図を求めてしまう方が良いのでしょうが、それをロバストに実装するのは難易度がそこそこ高いです(腕に覚えがある人は挑戦しても良いかも知れません)。
参考図書(計算幾何工学, 杉原厚吉, 培風館)
一方、Delaunay三角形分割は計算自体が元々誤差に対し強いので、特に工夫しなくともロバストさを期待できます。