『理論から学ぶデータベース実践入門』という本を読んでいて、2章の論理学の説明に多くの誤りを見つけたので指摘しておく。
この本はデータベースについての技術書であり、数学書ではないのでこれらの誤りがこの本の価値を完全に損なうとは思わない。しかし、述語論理に基いてリレーショナルモデルを説明するという趣旨の本である以上、その基礎である論理学の説明が不正確なのは大きな問題である。また著者が論理学の専門家でないなら、専門家にレビューを頼むか、最低でも適切な論理学の教科書へのリファレンスが必要ではないかと考える。
この文章は特定の本を参考にしたわけではないが、以下に定評のある論理学の入門書をいくつか挙げておく。
- 戸田山和久『論理学をつくる』(名古屋大学出版会)
- 小野寛晰『情報科学における論理』(日本評論社)
以下、論理学についての誤りのうち比較的大きなものを指摘する。これはすべての誤りのリストではないし、また著者の意図が本文に正しく反映されていない可能性もある。
論理的な矛盾とデータの不整合を混同している
著者は述語論理における矛盾とリレーショナルモデルにおけるデータの不整合を結びつけようとしている(2章、p. 52):
リレーショナルモデルは、述語論理のルールに支配されたデータモデルです。したがって、述語論理にとって厄介なことは、リレーショナルモデルでも起こり得ます。
述語論理にとって、最も厄介なことは矛盾です。前提に矛盾が含まれていると、Principle of explosionの定理により、どのような帰結でも導き出すことが可能になります。つまり、矛盾したデータを持つリレーションから導き出された問い合わせの結果は、まったく信用ならないということです。
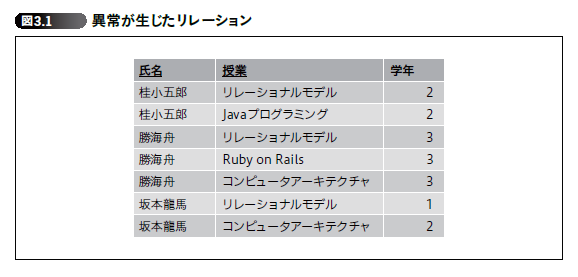
3章では具体的なテーブルの例を持ってきてこのことを議論している (p. 68):
図3.1のリレーションのどこに矛盾が生じているのでしょうか。このリレーションに登場する3 名のうちの1 名、坂本龍馬さんの学年に注目してください。
なんということでしょう! 坂本さんの学年には、2つの異なる値が格納されているではありませんか!
述語論理における矛盾 (e.g. $x \neq x$) に対応するのは空集合である。しかし図3.1に示されたリレーションは明らかに空集合ではない。ここで本来問題になっているのは論理的な矛盾ではなく、「1人の人間が異なる2つの学年をもつことはない」という大学のルールに対する不整合である。
また、第2章でもリレーションのJOINという操作の説明で矛盾について言及している (p. 56):
直積の場合は、2つのリレーションの要素のすべての組み合わせによって導出される命題が、新しいリレーションの要素となりましたが、共通の要素がある場合はそうはいきません。結合後のリレーションに含まれるタプルは、共通の属性の値が同じものだけです。なぜそうなるかと言うと、共通の属性は同じ意味を持っており、同じ値でなければ矛盾になるからです。たとえば、図2.4の2つのリレーションを結合する場合を考えてみましょう。
ここで「共通の属性は同じ意味を持っており、同じ値でなければ矛盾になるからです」が言おうとしているのは変数に対する割り当てが一貫している必要があるということだと思われるが、この概念は述語論理における矛盾とはまったく関係ない。
命題論理の限界についての説明がおかしい
著者は命題論理の限界を指摘し、そこから述語論理を導入している (p. 42):
命題論理は、突き詰めて言えば命題同士の関係性について、あれこれと考える学問です。ある事実を単に真偽値を持った命題として表現できる限りは、それで十分ですが、そうではない場合、つまり事実をシンプルな命題を用いて表現できないケースには対応できません。
たとえば、「この村のすべての村人が正直者だというわけではない」という文章は、どのような論理式で表現すれば良いでしょうか?
この文章をたとえば、P という命題だと仮定すると、「この村には正直でない者がいる」という命題の真偽は、どうやって証明すれば良いでしょうか? ほかにも「この村の村人は全員誰かと友だちである」という文章は、どのような論理式で表現すれば良いでしょうか? この文章と、「この村には村人全員と友だちの村人がいる」という文章との違いを、どのように確認すれば良いのでしょうか。
「この村のすべての村人が正直者だというわけではない」という文を命題変数 $P$ と置くのが不適当だという著者の主張は非常にミスリーディングである。
ある文を論理式でモデル化したいとき命題論理を使うべきか述語論理を使うべきかは文を見るだけでは分からない(「ソクラテスは人間である」を表すのに $P$ と $Hs$ どちらが適当だろう?)。命題論理と述語論理どちらを使うのが適当なのかは文ではなく分析したい推論によって決まる。このことについて簡潔に説明しよう。
# 推論1
仮定
- 雷が鳴ると雨が降る
- 雨が降ると地面が濡れる
結論
- 雷が鳴ると地面が濡れる
このような推論を「仮定 $P \rightarrow Q, Q \rightarrow R$ から結論 $P \rightarrow R$ が導かれた(略記:$P \rightarrow Q, Q \rightarrow R \vdash P \rightarrow R$)」とモデル化して分析するのが論理学である。じっさい真理値表を書いてみれば $(P \rightarrow Q) \land (Q \rightarrow R) \rightarrow (P \rightarrow R)$ がトートロジーになることが分かる。
いま見たように命題論理は命題の内部構造については関知せず、もっぱら命題と命題の関係を調べる。一方述語論理は命題論理を拡張して命題の内部構造についても扱えるようにした論理である。それによって次のような分析が可能になる。
# 推論2
仮定
- すべての人はすべての人を愛している
結論
- アリスはボブを愛している
この推論を述語論理でモデル化すると「$\forall x \forall y Lxy \vdash Lab$」ということになる。このことに対応して $\forall x \forall y Lxy \rightarrow Lab$ は一階述語論理の恒真式になっている。
このように論理学的分析の基本単位になるのは命題そのものではなく「$A_1, \dots, A_n \vdash C$」という形式の推論である。また、これに対応して $A_1 \land \dots \land A_n \rightarrow C$ という形の恒真式(トートロジー)ができる。したがって分析の基本単位は恒真式であると言ってもよい。「ソクラテスは人間である」や「この村のすべての村人が正直者だというわけではない」は論理的真理ではなく世界で成り立っている事実に関わることなので、この文だけを見て命題論理と述語論理どちらで表すのが適当か決めることはできない。
古典論理の定義を間違えている
古典論理は一階述語論理の別名であるという記述があるがこれは誤りである (p. 49):
これまで紹介してきた述語論理は、正確には一階述語論理と呼びます。一階述語論理は、古典論理とも呼ばれます。
この本で扱われている命題論理と一階述語論理が古典論理だというのは正しいが、直観主義命題論理、直観主義一階述語論理などの古典論理でない論理も存在する。
集合と集合論、述語と述語論理を混同して使っている
- p. 49「述語と集合は1対1対応します」
- p. 50「集合は一階述語論理と1:1対応する」
- p. 64「述語論理と集合論は1:1で対応しています」
1つ目の主張は正しいが、2つ目と3つ目は比べられている対象のカテゴリーが異なるので意味のない主張になっている。これ自体は記述を直せばいいだけの問題なので大したことはないが、そのせいで全体的に混乱した記述になっている。
二階論理の説明がおかしい
筆者は二階論理の特徴として自己言及が可能であると述べている (p. 49 - p. 50):
二階述語論理は、述語の特徴を表現する述語を扱うのが特徴です。たとえば、「x は、真となるパラメータが1つ以上存在するが、恒真ではない述語である」といった具合です。述語と集合は1対1で対応しますので、二階述語論理は、集合を要素にした集合を扱うものであると言えます。
述語自身を述語の対象にすると、自分自身もその述語の対象になり得ます。先ほどの「xは、真となるパラメータが1つ以上存在するが、恒真ではない述語である」という述語は、自身を評価すると真になるでしょう。このように、自己言及があるというのも二階述語論理の特徴です。二階述語論理はもちろん、一階述語論理よりも表現力が豊かですが、その分複雑になります。
しかしここで述べられているような自己言及は二階論理では不可能である。「$x$は、真となるパラメータが1つ以上存在するが、恒真ではない述語である」というのは次のような二階の述語 $R(X) := \exists x X(x) \land \neg \forall y X(y)$ であると思われる。
「述語自身を述語の対象にすると、自分自身もその述語の対象になり得ます」と書いてあるが、$R(X)$は二階の述語であるので$X$には一階の述語しか代入することはできない。
このようなことをするには(ナイーブな)包括原理を導入する必要がある。しかしよく知られたようにナイーブな包括原理を導入した体系はラッセルのパラドックスを引き起こす。このことについては説明しないので、例えば以下の情報源にあたってほしい。
- 三浦俊彦『ラッセルのパラドクス』
- Russell's Paradox (Stanford Encyclopedia of Philosophy)
- ラッセルのパラドックス:傾向と対策 (1) - あいまいな本日の私(旧)
謝辞
otb_btb氏のレビューによって原稿の誤りをいくつか訂正できた。この場で感謝したい。