全加算器について勉強しました

前書き

最近は【Code: The Hidden Language of Computer Hardware and Software】という本を読んで、
結構面白いと思って、この中に書いた Adder を作るプロセスをシェアしたいと思います。

論理回路（Logic Gate）

NOT Gate

x	result
0	1
1	0

OR Gate

x	y	result
0	0	0
0	1	1
1	0	1
1	1	1

AND Gate

x	y	result
0	0	0
0	1	0
1	0	0
1	1	1

NAND Gate 　

AND Gateの真逆です。

NAND は AND と NOT で作っています。

x	y	result
0	0	1
0	1	1
1	0	1
1	1	0

半加算器

今回は A と B を加算するプロセスを説明します。
A と B は 1-bit です。

たぶん気づいたと思いますが、
A と B の加算結果が、

A	B	sum
0	0	0
0	1	1
1	0	1
1	1	10

になります。

しかし、今作成しようとする加算器は 1-bit しか対応していないので、
A と B 両方が 1 になった場合に、
計算結果が Overflow します。

この状況を対応するため、
A と B の加算結果を sum 以外に、carry も保存するべきです。

A	B	sum	carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Carry

carry の部分について簡単で、
前に話したAND Gateとぴったりですね。
そのまま利用できます。

Sum と XOR

Sum の部分について、既存の論理回路ではそのまま利用できなさそうですね。

OR GateとNAND Gateの場合に、A と B のどっちが 1 の場合に、結果が 1 になる、
また、A と B 両方が 0 の場合に、NAND Gateが 1 になり、
逆に、A と B 両方が 1 の場合に、OR dateが 1 になります。

A	B	OR	NAND
0	0	0	1
0	1	1	1
1	0	1	1
1	1	1	0

じゃあ、A と B がOR GateとNAND Gateを通った結果をまたAND Gateでもう一度計算すると、
期待通りになりそうですね。

A	B	OR	NAND
0	0	0	1
0	1	1	1
1	0	1	1
1	1	1	0

OR	NAND	AND
0	1	0
1	1	1
1	1	1
1	0	0

上記のような計算ロジックをXORと言います。

XOR	0	1
0	0	1
1	1	0

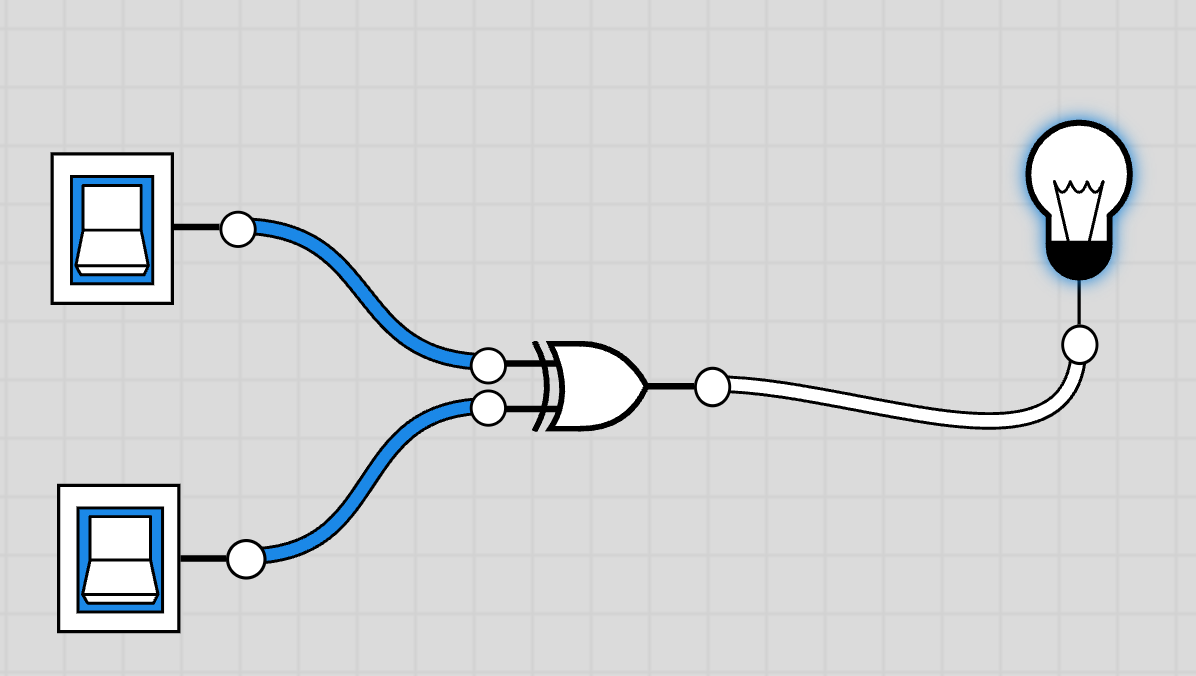
XOR も自分の記号があります。

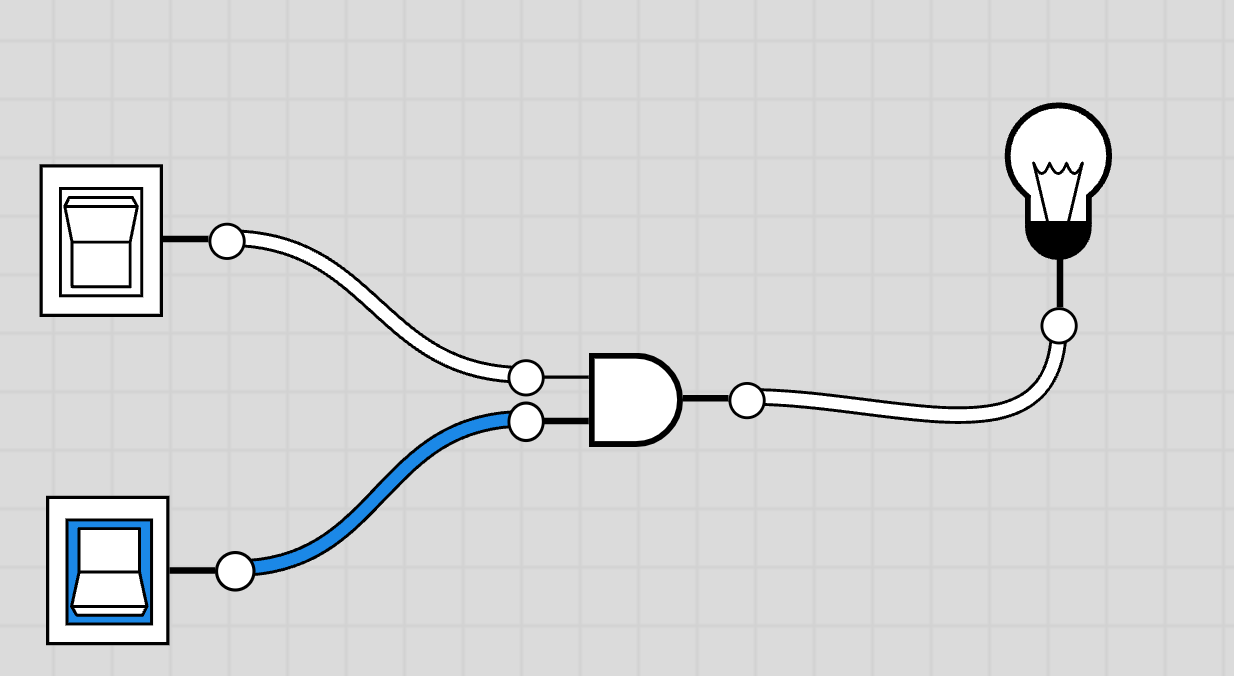
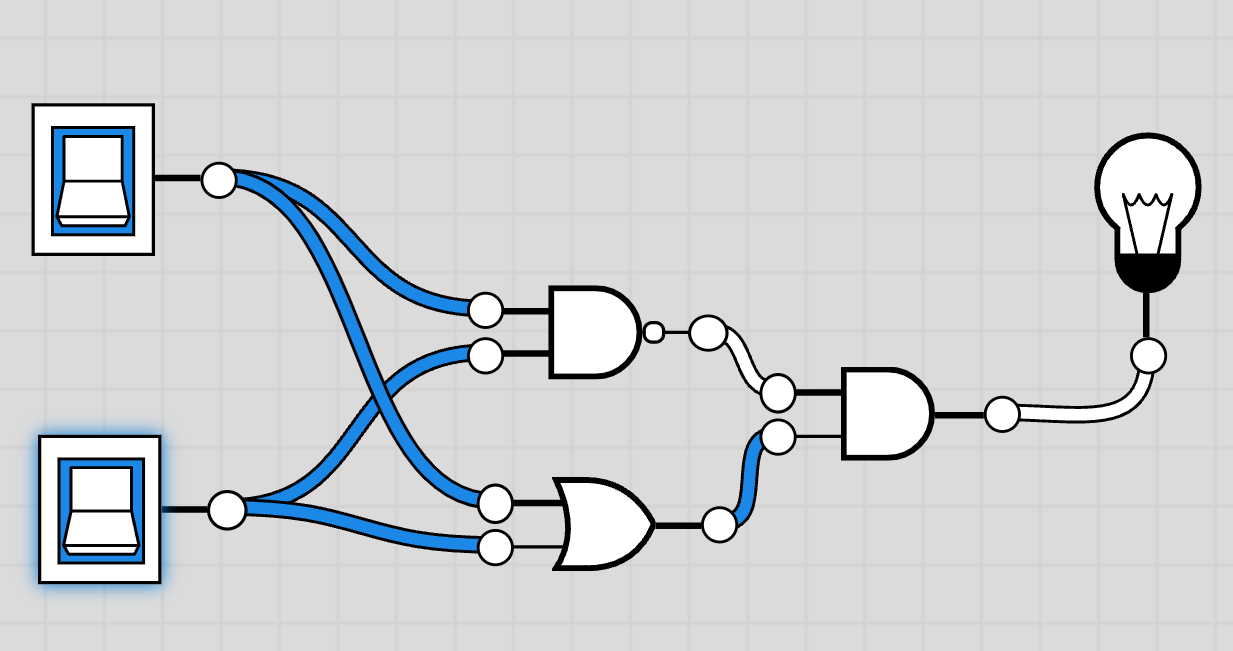
ここまでに行くと、Logic Gateを使って半加算器を実現できました。

上の電球が Sum、下の電球が Carry。

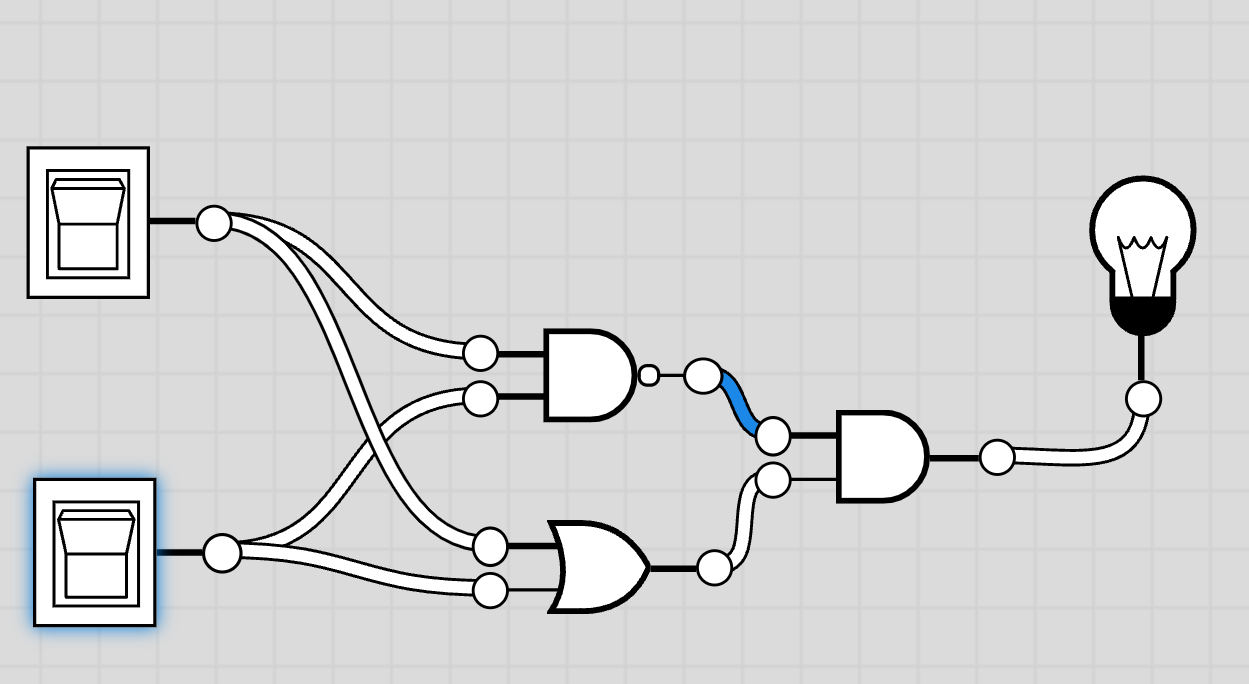
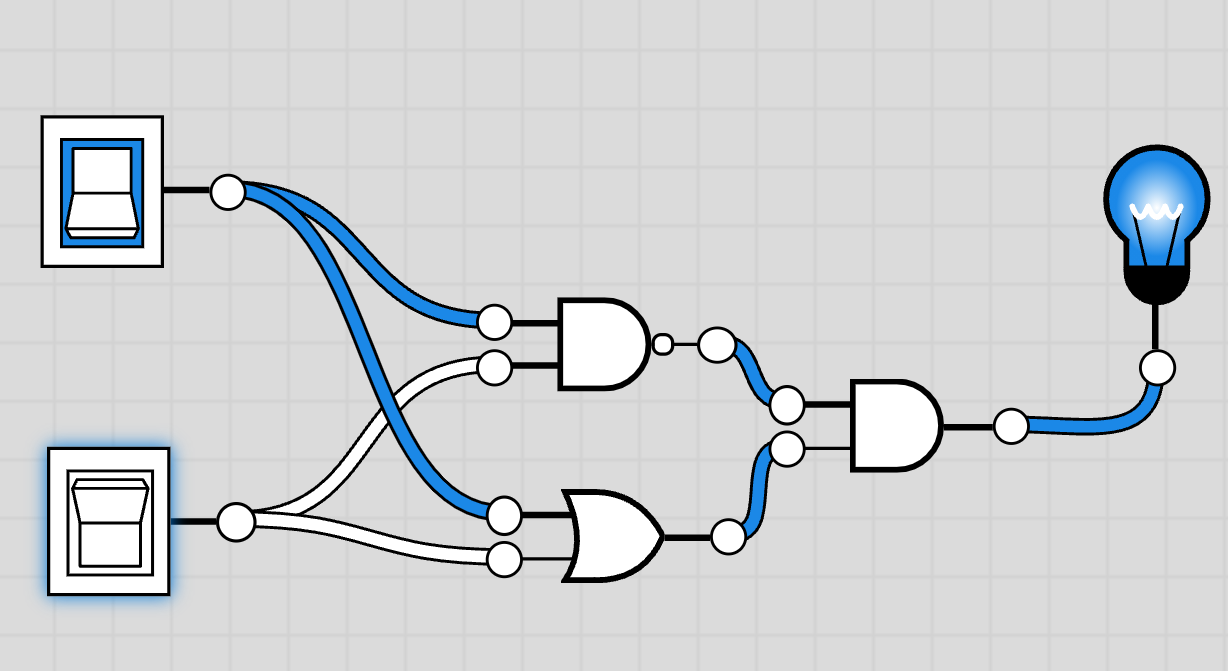
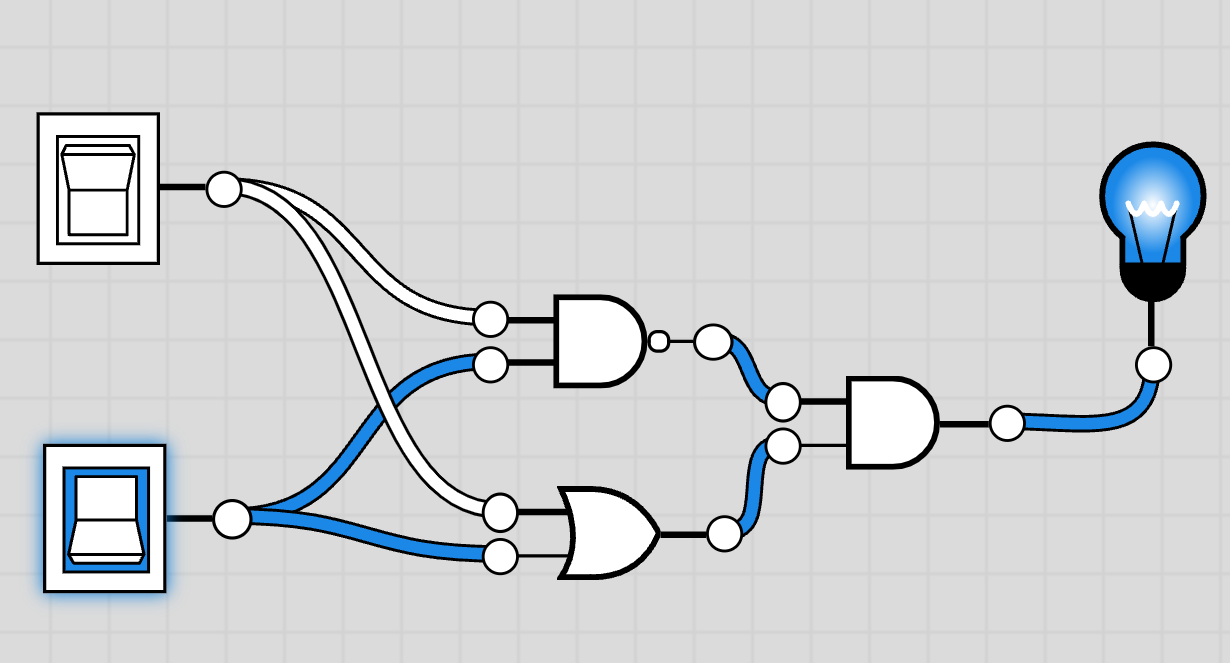
全加算器

半加算器では、A と B の計算で桁上げが発生する場合に、桁上げを上位桁に利用できます。
こういう風に繰り返しますと、
1-bit ではなく、
何 bit でも、最下位から最上位まで計算できます。

結論で言うと、全加算器が 1-bit の数値を計算する物ですが、
複数の全加算器を並べると、数 bit の数値を計算することができます。
例えば、8 個の全加算器を利用すると、8-bit の数値を計算でき、
最大 2^8-1=255 まで計算できます。

全加算器の INPUT が A と B 以外に、下位桁からの Carry も INPUT として利用します。

まず最終的なイメージ（実現したいこと）をここに書きます。

A	B	C:input	sum(final)	C(final)
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

sum(final)

A	B	sum(A+B)	C:input	sum(final)	C(final)
0	0	0	0	0	0
0	1	1	0	1	0
1	0	1	0	1	0
1	1	0	0	0	1
0	0	0	1	1	0
0	1	1	1	0	1
1	0	1	1	0	1
1	1	0	1	1	1

sum(A+B)	C:input	sum(final)
0	0	0
1	0	1
0	1	1
1	1	0

重複な部分をいったん削除します。

なんか見覚えがあるのではないですか？

NOTE A+B は半加算器で計算しています。

そうです、A と B の計算結果 + C:input がまさに半加算器で、最終的な Sum を計算できます。

つまり、

半加算器2(半加算器1(A, B), C:input) = sum(final), 半加算器2 C:output

A	B	sum(A+B)	C:input	sum(final)	半加算器 2 C:output	C(final)
0	0	0	0	0	0	0
0	1	1	0	1	0	0
1	0	1	0	1	0	0
1	1	0	0	0	0	1
0	0	0	1	1	0	0
0	1	1	1	0	1	1
1	0	1	1	0	1	1
1	1	0	1	1	0	1

この半加算器の Carry（output）の部分も上記のように埋めます。

C:output

A と B が半加算器 1 での計算結果を補足します。

A	B	sum(A+B)	半加算器 1 C:out	C:in	sum(final)	半加算器 2 C:out	C(final)
0	0	0	0	0	0	0	0
0	1	1	0	0	1	0	0
1	0	1	0	0	1	0	0
1	1	0	1	0	0	0	1
0	0	0	0	1	1	0	0
0	1	1	0	1	0	1	1
1	0	1	0	1	0	1	1
1	1	0	1	1	1	0	1

ここまで行くと、
最後に計算したいことがC:outです。

どのデータを使ってC:outを計算できるでしょうか？

半加算器 1 C:out	半加算器 2 C:out	C(final)
0	0	0
0	0	0
0	0	0
1	0	1
0	0	0
0	1	1
0	1	1
1	0	1

重複な部分を削除します。

半加算器 1 C:out	半加算器 2 C:out	C(final)
0	0	0
1	0	1
0	1	1

半加算器 1 C:outと半加算器 2 C:outが同時に 1 になるケースがないですが、
これを見ると、OR Gateが使えそうと思いますね。

そうです。
二つの半加算器のC:outをまたOR Gateの二つの Input として使って、
OR Gateの Output が最終的のC(final)になります。