これはKMC Advent Calendar 2019の12日目の記事として書かれました
zekeです。この記事は自身がAtCoderのEDPC(Educational DP Contest / DP まとめコンテスト)で解いた問題の解法の備忘録的な立ち位置で書かれています。
自分は競技プログラミング初心者なので、間違いなどがありましたら遠慮なくご指摘ください。
まず初めに
AtCoderのコンテストでは頻出のDP。競技プログラミングにおける動的計画法にはさまざまな種類があると思います。ナップサックDPを始めとして、期待値DP、ゲームDP…自分も勉強中ですが、この分野は大変奥が深いように思われます。そこで今回は自己鍛錬のためにもEDPCのA問題からM問題13問の解説をやっていこうと思います。
また記事の性質上、ネタバレを含むことに注意してください。
DPについての独り言
動的計画法の根本的な考え方について初心者ながら理解していることを語ります。
まずwikiで動的計画法について調べると、「対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法」と書かれてあります。よくわかりませんね。具体例を出してみましょう。フィボナッチ数列をご存じですか?直前の二つの項を足していく数列のことです。1,1,2,3,5,8,13…と続きます。これを動的計画法の観点から見ていこうと思います。例えば第5項を求めるにはどうすればいいですか?もちろん第3項と第4項を足しますよね。それでは第3,4項を求めるには?同じように前二項を足します。今、何をしていたかというと「第5項を求める」という問題を「第3,4項を求める」という部分問題に分割しました。しかも、第5項の値は一度計算したら、もう一度計算する必要はありません。そこで計算結果を配列などに記録することをします。
長くなりましたが、動的計画法の肝は項のような「状態」と状態をつなぐ「漸化式」にあると思います。そこでこの解説では、この二つを明確にしていこうと思います。
DP問題を考える際に
- 状態を考える
- 次元
- 中身
- 0-index,1-index
- 典型に落とす
- 漸化式を考える
- 最大値、最小値をとる
- 足す、差を取る、掛ける(MOD計算)
- 貪欲
- 場合分け
- 例外処理
- 計算量を考える
- 次元を下げてみる(計算量を落とす)
- 軸を変えてみる
- 中身を変えてみる(型を変えてみる)
- for文の中身を外に出す(前処理)
- ループの順番を変えてみる
を考えるといいかもしれません。
目次
A-Frog 1 DPの基本!
B-Frog 2 進化したカエル
C-Vacation 初めての二次元DP
D-Knapsack 1 定番!ナップサックDP!
E-Knapsack 2 重くなったナップサック
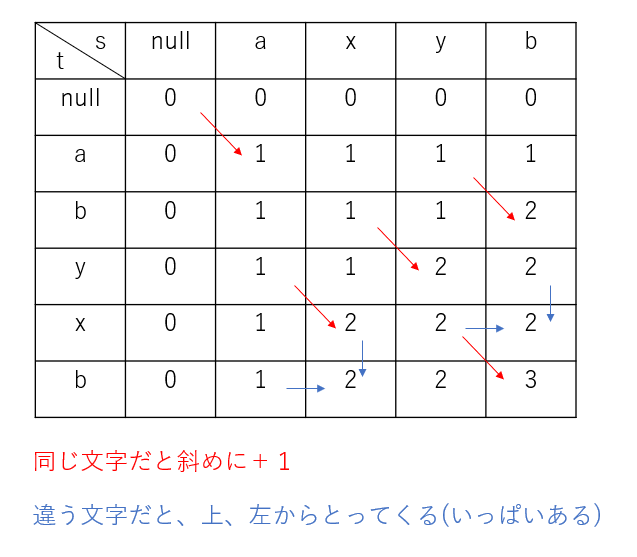
F-LCS 文字列の登場
G-Longest Path グラフ…!
H-Grid1 迷路
I-Coins 確率DP
J-Sushi 期待値DP
K-Stones ゲームDP
L-Deque 区間DP
M-Candies 累積和
このようにM問題まで解説していきます。
A問題-Frog1
(https://atcoder.jp/contests/dp/tasks/dp_a)
栄えある一番目を飾るのはフィボナッチみたいな数列です。DPの超基本問題ですね。とりあえず、図にして整理してみましょう。
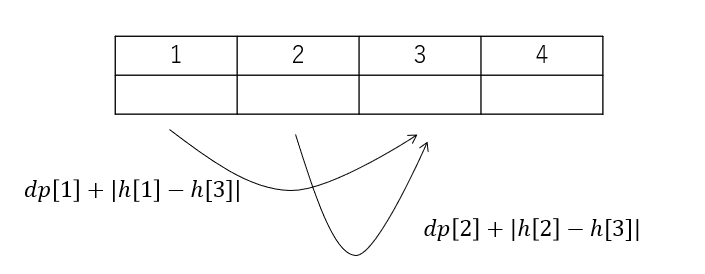
図にある通り、項の直前の二つを見てあげればよさそうです。
状態は
dp[i]:i番目まで行くのに必要な最小コスト
でよさそうです。
漸化式で表記すると、
dp[i]=\min ( dp[i-1]+|h[i-1]-h[i]|,dp[i-2]+|h[i-2]-h[i]| )
簡単なコード
vector<int> dp(n);
dp[0]=0;
dp[1]=abs(h[1]-h[0]);
for(int i=2;i<n;i++){
dp[i]=min(dp[i-1]+abs(h[i]-h[i-1]),dp[i-2]+abs(h[i-2]-h[i]));
}
計算量はO(n)です。
一応、今は「もらうDP」をやっています。
B問題-Frog2
(https://atcoder.jp/contests/dp/tasks/dp_b)
今度のカエルは2つとは言わずK個先まで飛べるようです。
なので、漸化式だけをいじるだけでいけそうですね!
dp[i]=\min(dp[j]+|h[i]-h[j]|)(max(i-k,0)\leq j \leq i-1)
コード
vector<int> dp(n,1e9+100);//十分大きな数字で初期化しておきます
dp[0]=0;//0番目(最初)はコスト0で行けます。
for(int i=0;i<n;i++){
for(int j=0;j<=k;j++){
if(i-j<0)break;//忘れないように!
chmin(dp[i],dp[i-j]+abs(h[i]-h[i-j]));
}
}
ちなみに
bool chmin(T &a, const T &b)
{
//b>aの時、aをbに更新
if (b < a)
{
a = b;
return 1;
}
return 0;
}
はDPにおいてよく使うので、持っておくと便利です。
計算量はO(NK)です。
C問題-Vacation
(https://atcoder.jp/contests/dp/tasks/dp_c)
太郎君が夏休みを満喫するようです。夏休みが最大100000日あるのいいな…。
状態としてまず
dp[i]-i日目までに太郎君が得る満足度の合計
を考えます。
しかし、「2日以上連続で同じ活動を行うことはできません」という条件をこのままでは漸化式で表せません。そこで状態を
dp[i][j]-i日目にj(0:A,1:B,2:C)をするとき、i日目までに太郎君が得る満足度の合計
を考えます。先ほどと違って二次元配列になりましたね。
図はいる
漸化式は
dp[i][0]=min(dp[i-1][1]+a[i],dp[i-1][2]+a[i]) \\\
dp[i][1]=min(dp[i-1][0]+b[i],dp[i-1][2]+b[i]) \\\
dp[i][2]=min(dp[i-1][0]+c[i],dp[i-1][1]+c[i]) \\\
となります。
コード例
vector<vector<int>> dp(n+1,vector<int>(3));
dp[0][0]=0;
dp[0][1]=0;
dp[0][2]=0;
for(int i=1;i<n+1;i++){
dp[i][0]=max(dp[i-1][1]+A[i-1],dp[i-1][2]+A[i-1]);
dp[i][1]=max(dp[i-1][2]+B[i-1],dp[i-1][0]+B[i-1]);
dp[i][2]=max(dp[i-1][0]+C[i-1],dp[i-1][1]+C[i-1]);
}
計算量は$O(N)$です
D問題-Knapsack1
(https://atcoder.jp/contests/dp/tasks/dp_d)
出ました!DPと言えばコレ!ナップサックDP!王道DPですね。
さて、太郎君は限られたナップサック容量の中で、できるだけ持って帰る価値の総量を大きくしたいようです。まず状態を考えましょう。ここでポイントなのが、配列を決める際にサイズが大きすぎるようにしないようにしましょう。配列を埋める分、時間がかかるので、大きくても$10^8$ぐらいにとどめましょう。このことを踏まえながら
dp[i][j]-i番目までの品物を見た時、重さの総量j以下に収まる最大価値
という状態を考えてみます。
図で考えてみると…
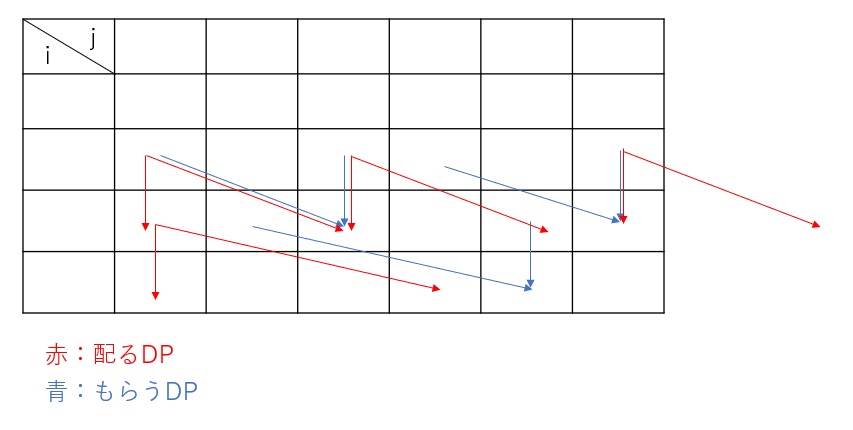
このように二通りの推移の仕方があるのが分かりますね!
漸化式は
dp[i][j] = dp[i-1][j] \\\
dp[i][j] = max(dp[i][j],dp[i][j-w_i]+v_i)(ただしw_i \leq j)
これはもらうDPとして考えています。
配るDPとして考えるならば、
dp[i+1][j]=max(dp[i+1][j],dp[i][j]) \\\
dp[i+1][j+v_{i+1}]=dp[i][j]+w_{i+1}
となります。重さの和がWを超えるので配列を取るときに十分に大きくとってください。
実装する上で、添字には気を付けてください。
普通に配列を取ると、1番目の商品の重さは配列の0番目です。
コード例(もらうDP)
vector<vector<long long>> dp(n+1,vector<long long>(w+1,0));
for(int i=1;i<n+1;i++){
for(int j=0;j<w+1;j++){
dp[i][j]=dp[i-1][j];
if(j-wei[i-1]>=0){
dp[i][j] = max(dp[i][j],dp[i-1][j-wei[i-1]]+val[i-1]);
}
}
}
コード例(配るDP)
vector<vector<long long>> dp(n +1, vector<long long>(w + 1e6, 0));
for (int i = 0; i < n ; i++)
{
for (int j = 0; j < w + 1; j++)
{
chmax(dp[i + 1][j], dp[i][j]);
dp[i+1][j+wei[i]] = dp[i][j]+val[i];
}
}
cout<<dp[n][w]<<endl;
どちらにせよ計算量は$O(NW)$です。
配るDP,もらうDPどちらでもできます。
今後の問題は臨機応変に(気分で)使い分けたいと思います。
E問題-Knapsack2
(https://atcoder.jp/contests/dp/tasks/dp_e)
さて、今度の問題はさっきと何が違うのでしょうか?よく見ると制約が変わってますね。
DではWが$10^5$程度だったのが、$10^9$になっています。これでは、さっきのままだとNW=$10^{11}$になってしまって、絶対間に合いませんね。しかし、今度は荷物の価値が$10^3$と小さくなっています。ここから状態を考えると…
dp[i][j]-i番目までの品物を見て、合計価値jを得るために必要な最小の重さ
と考えたらよさそうです。さっきと軸が変わりました。
漸化式は、配るDPで考えると
dp[i+1][j]=min(dp[i+1][j],dp[i][j]) \\\
dp[i+1][j+v_{i+1}]=dp[i][j]+w_{i+1}
価値の軸は最大$\sum v_i$つまりは、$10^3$*$10^2$=$10^5$になることに注意しましょう。
コード例
vector<vector<int>> dp(n + 1, V(1e6, 1e18));//配列のサイズ大きめに、大きな数字で初期化しておきましょう
dp[0][0] = 0;//最初は0です
for (int i = 0; i < n;i++){
for(int j = 0;j<1e5+1, j++){
chmin(dp[i + 1][j], dp[i][j]);
chmin(dp[i + 1][j + val[i]], dp[i][j] + wei[i]);
}
}
答えは$dp[n][j]$の$j$の大きいほう、価値の大きいほうから見ていって初めて$W$を下回った時の$j$になります。
計算量は$O(N\sum v_i)$です。
F問題-LCS
(https://atcoder.jp/contests/dp/tasks/dp_f)
LCS-最長共通部分列です!二つの文字列s,tが与えられるので、最長の共通部分列を求めます。この時、状態をこのように取ります。
dp[i][j]-文字列sをi番目まで見た時、文字列tをj番目まで見た時、最長の共通部分列長
漸化式は
dp[i][j] = \left\{
\begin{array}{ll}
0(i= 0 or j = 0) \\\
dp[i-1][j-1]+1(s[i]\equiv t[j]) \\\
max(dp[i-1][j],dp[i][j-1])(s[i] \neq t[j])
\end{array}
\right.
int dp[s.length()+1][t.length()+1];
for(int i=0;i<(int)s.size()+1;i++){
for(int j=0;j<(int)t.size()+1;j++){
if(i==0 || j==0){
dp[i][j]=0;
}
else if(s[i-1]==t[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
これで終わりじゃないのが、この問題の難しいところ。長さはわかったんだけど、それを復元しないといけない。
この時、重要なのは「更新したポイント」。つまり$s[i] \equiv t[i]$が成立しているときに1だけ共通部分列が伸びてるから、そこを後ろから見ていけばいい。
図で見ると分かりやすいかも
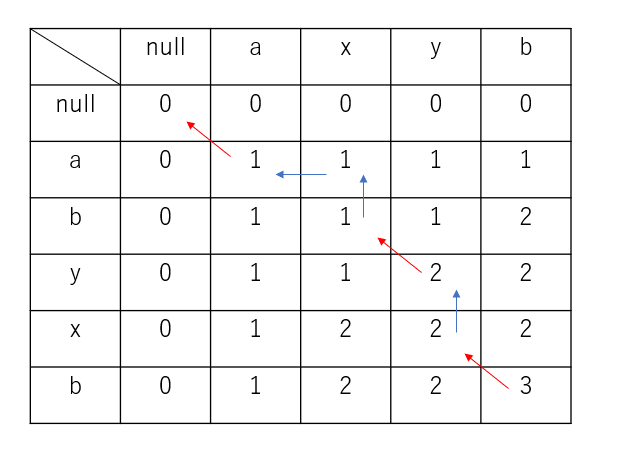
コード例
int i = s.size();
int j = t.size();
int ans_length = dp[i][j];//最長共通部分列長
vector<char> result(ans_length);//答えを持つ配列
while (i > 0 && j > 0){
if (s[i - 1] == t[j - 1]){
result[ans_length - 1] = s[i - 1];
ans_length--;i--;j--;
}else if (dp[i - 1][j] > dp[i][j - 1]){//さっきの漸化式を逆に辿るイメージ
i--;
}else{
j--;
}
}
計算量は$O(|s||t|)$です。
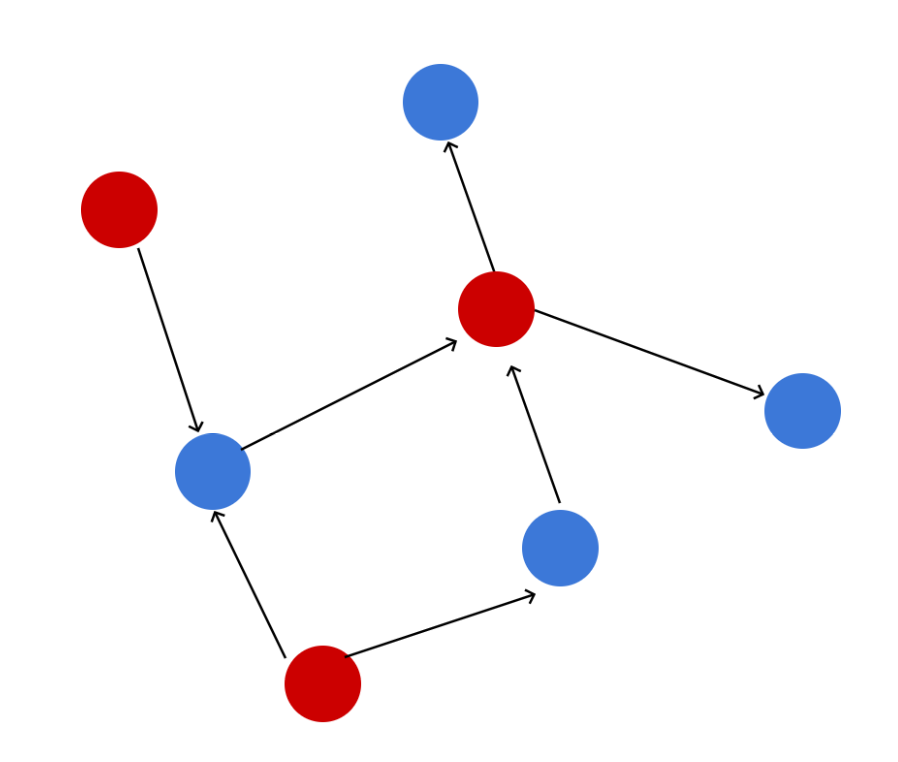
G問題-Longest Path
(https://atcoder.jp/contests/dp/tasks/dp_g)
有向グラフ内の最長パスを求めたいです。
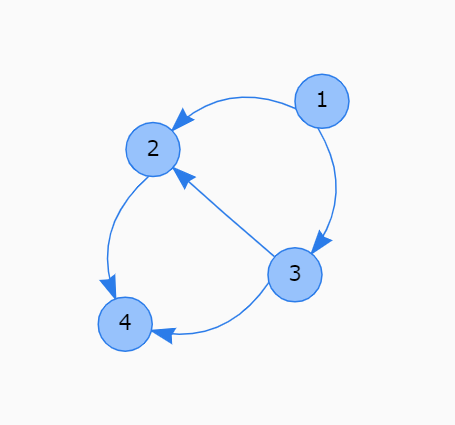
例えば、上の図では(1,3,2,4)と進むと長さ4のパスが得られます。
状態としては
dp[i]-頂点iから始まる最長パス長
これは「メモ化再帰」を使うと簡単に書けます。
漸化式は
dp[i] = \left\{
\begin{array}{ll}
0(iが葉、例だと頂点4の時) \\
max\bigl\{dp[j]+1|jはiの行先\bigr\}
\end{array}
\right.
最長パスが決まった頂点にメモをしていく再帰ですね!
int dp[100001];//DP配列
vector<vector<int>> gragh;//二次元隣接リスト
int rec(int k)
{
if (dp[k] != -1){
return dp[k];//もし探索済みだったらそのまま返す
}else{
int res = 0;
for (int i = 0; i < gragh[k].size(); i++){
chmax(res, rec(gragh[k][i]) + 1);//グラフの行先をみて+1する
}//この時、行先がない(=葉だった)場合0を返すことになる
return dp[k] = res;
}
}
int main()
{
int n, m;
cin >> n >> m;
gragh.resize(n);
for (int i = 0; i < m; i++){
int x, y;
cin >> x >> y;
x--;y--;//グラフのときは0から始める派です
gragh[x].push_back(y);
}
for (int i = 0; i < n; i++)dp[i] = -1;//まずは全頂点未探索を意味する-1を入れておきます
int res = 0;
for (int i = 0; i < n; i++){
chmax(res, rec(i));//各頂点からの最長パスを見ます。
}
cout << res << endl;
}
計算量は、頂点と辺を高々1回しか見ないので$O(N+M)$
H問題-Grid1
(https://atcoder.jp/contests/dp/tasks/dp_h)
太郎君が(1,1)から(H,W)まで行きたいそうです。何通りありますか?この時状態を
dp[i][j]-(0,0)から(i,j)への行き方の数
実装の都合上、0indexにしています。
太郎君は右か下に進めないので、漸化式は
dp[i][j]=0(a_{i,j}\equiv \#)\\\
dp[i][j]=dp[i][j]+dp[i][j-1](j\geq 1)\\\
dp[i][j]=dp[i][j]+dp[i-1][j](i\geq 1)
小学生のころ、同じことを手計算でやった気がする…?
コード例
vector<vector<int>> vec;
vector<vector<int>> dp;
int h, w;
void rec(int y, int x){
if (vec[y][x] == '#')return; //壁だったら考えるまでもないです
if (y >= 1){//下へ行きます
if (vec[y][x] == '.'){
dp[y][x] += dp[y - 1][x];
dp[y][x] %= MOD;
}
}
if (x >= 1){//右に行きます
if (vec[y][x] == '.'){
dp[y][x] += dp[y][x - 1];
dp[y][x] %= MOD;
}
}
}
int main(){
cin >> h >> w;
vec.resize(h, vector<int>(w));
dp.resize(h, vector<int>(w));
for (int i = 0; i < h; i++){
string s;
cin >> s;
for (int j = 0; j < w; j++){
vec[i][j] = s[j];
}
}
dp[0][0] = 1;//スタート位置への行き方は1です。
for (int i = 0; i < h; i++){
for (int j = 0; j < w; j++){
rec(i, j);//左上から右下へと埋めていくイメージです
}
}
cout << dp[h - 1][w - 1] % MOD << endl;
}
MODを取るのを忘れずに。
計算量は$O(HW)$です。
I問題-Coins
(https://atcoder.jp/contests/dp/tasks/dp_i)
確率DPですね。確率という言葉にビビる必要はないです。状態を
dp[i][j]-i枚投げてj枚表の確率
と定義すると、漸化式は
dp[i][j]=\left\{
\begin{array}{ll}
dp[i-1][j]*(1-p_i)(j=0) \\
dp[i-1][j-1]*p_i+dp[i-1][j]*(1-p_i)(j \neq 0)
\end{array}
\right.
となります。表を出したとき、裏を出したとき、それぞれを考えてやればいいです。
コード例
int main(){
int n;
cin >> n;
vector<double> P(n);//今回は小数がでてくるのでdouble型を取っておきましょう
for (int i = 0; i < n; i++)cin >> P[i];
double dp[n + 1][n + 2];
dp[1][0] = 1 - P[0];//初期化をしていきましょう
dp[1][1] = P[0];
for (int i = 2; i <= n; i++){
for (int j = 0; j <= i; j++){//投げたコイン以上の表のコインは出ないのでiまでしか回さない
if (j == 0){
dp[i][0] = dp[i - 1][0] * (1 - P[i - 1]);//0枚表の時だけ別です
}else{
dp[i][j] = dp[i - 1][j - 1] * P[i - 1] + dp[i - 1][j] * (1.0 - P[i - 1]);
}//dp[i][j]=「表の時」+「裏の時」
}
}
double res = 0;
for (int i = n / 2 + 1; i <= n; i++){
res += dp[n][i];
}//表のほうが多い確率なので、該当するものをすべて足し上げています
cout << setprecision(10) << res << endl;
}
計算量は$O(N^2)$です。
J問題-Sushi
(https://atcoder.jp/contests/dp/tasks/dp_j)
期待値DPです。個人的に前半の中で最も難しいと思います。
まずは状態なのですが、皿同士の区別がないので、
dp[i][j][k] : 残りの寿司1個の皿がi個、2個の皿がj個、3個の皿がk個の時、寿司がなくなるまでの操作回数の期待値
と考えてみたいと思います。
例を挙げます。
もし$dp[0][0][0]$の時は?
残っている寿司が0なので、期待値も0に決まってます。
それでは、$dp[1][0][0]$は?
いま寿司が1つ乗っている皿が一つある状態ですね。
N枚の皿から皿をランダムで選んでいるので、
dp[1][0][0]=dp[0][0][0]* \frac{1}{N} +dp[1][0][0]* \frac{N-1}{N}+1
次にどの状態へ移り変わっていくか?というイメージです。
最後の「+1」は、いままさに1回の操作をするという意味です。
j=0,k=0の時、一般化してみると
dp[i][j][k]=dp[i-1][j][k]*\frac{i}{N}+dp[i][j][k]*\frac{N-i}{N}+1
いま残りの寿司1個だけを考えていましたが、より一般的に考えると、
dp[i][j][k]=dp[i][j][k]*\frac{N-i-j-k}{N}+dp[i-1][j][k]*\frac{i}{N}+dp[i+1][j-1][k]*\frac{j}{N}+dp[i][j+1][k-1]*\frac{k}{N}+1
と考えられます。
残り2枚の皿を$\frac{j}{N}$の確率で選択して、残り2枚の皿を1つ減らし。残り1枚の皿を1つ増やす
残り3枚の皿を$\frac{k}{N}$の確率で選択して、残り3枚の皿を1つ減らし。残り2枚の皿を1つ増やす
といったことを式にしました。
しかし、まだ漸化式は完成していません。
なぜなら$dp[i][j][k]$が両辺に出現しているからです。
自身を求めるのに、自身を参照してしまっているので、式変形を行って
dp[i][j][k]=\frac{(N+dp[i-1][j][k]*i+dp[i+1][j-1][k]*j+dp[i][j+1][k-1])}{i+j+k}
とあらわすことができます。
あとは、コードを書くだけなのですが、いろんなところから参照しているので、メモ化再帰で書くのがよさそうです。
「-1」しているので、配列外参照には気を付けてください。
また、小数が出てくることにも気を付けてください。
long double n;
long double dp[301][301][301];//dp配列です、制約は300以下です
long double cal(int i,int j,int k){//再帰関数です
if(dp[i][j][k]!=-1)//すでに計算していたら、それを返します
return dp[i][j][k];
if(i==0&&j==0&&k==0)
return 0.0;//上の例を見てください
long double res = n;
if(i>=1)
res += cal(i - 1, j, k) * i;
if(j>=1)
res += cal(i + 1, j - 1, k) * j;
if(k>=1)
res += cal(i, j + 1, k - 1) * k;
res /= (i + j + k);//漸化式を見てください
return dp[i][j][k] = res;
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
int l1 = 0;int l2 = 0;int l3 = 0;
for (int i = 0; i < n;i++){
int x;
cin>>x;
if(x==1)
l1++;
if(x==2)
l2++;
if(x==3)
l3++;
}//l1が寿司が残り1個の、l2が2個の。l3が3個の皿の数です
for (int i = 0; i < 301;i++)
for (int j = 0; j < 301;j++)
for (int k = 0; k < 301;k++)
dp[i][j][k] = -1;//あらかじめ-1で初期化しておきます。
cout << setprecision(10) << cal(l1, l2, l3) << endl;
}
計算量は$O(N^3)$です。
K問題-Stones
(https://atcoder.jp/contests/dp/tasks/dp_K)
今度はゲームDPです。これはゲームの基本なのですが、
(勝ち状態)-負け状態を相手に渡すことができる=遷移先に少なくとも一つの負け状態がある\\\
(負け状態)-負け状態を相手に渡すことができない=遷移先がないor遷移先はすべて勝ち状態
こう考えることで、今プレイヤーが持つ状態から勝てるのか、負けるのかを推測可能です。
このゲーム理論に関しては、詳しく話すと本が一冊できるので省きます。(そもそも話せない)しかし、この問題を解く上では以上の説明で十分です。つまり状態を、
dp[i]-石がi個残っている状態は勝ち状態か負け状態か
と定義してやって、石の少ないほうから見てやればいいです。
コード例
int main(){
int n, k;
cin >> n >> k;
V vec(n);//V=vector<int>です
V dp(k + 1,-1);//まず最初に未確定のしるしとして-1を入れておきます
for (int i = 0; i < n;i++)cin >> vec[i];
dp[0] = 0;//まず残りの石が0個の時は負けなのは自明
for(int i=1;i<=k;i++){
bool h = false;//遷移先に負け状態があるかどうかのフラグです
for (int j = 0; j < n;j++){
int k = i - vec[j];
if (k >= 0 && dp[k] == 0)h = true;//もし負け状態があったならフラグを立てます
}
if (h)dp[i] = 1;//勝ち状態です、1を入れます
else dp[i] = 0;//負け状態です。0を入れます
}
if (dp[k])cout << "First" << endl;
else cout << "Second" << endl;
}
ゲーム理論に関してはDP以外にも$O(1)$の問題がよくあるイメージです。
計算量は$O(NK)$です。
L問題-Deque
(https://atcoder.jp/contests/dp/tasks/dp_L)
この問題は少し難しいですね。ゲーム理論のミニマックス法の問題のようです。片方が最大化しようとし、もう片方が最小化しようとするものですね。このゲームは両端から数を取っていくので、状態を
dp[i][j]-区間[i,j)が残っているとき両者が最善を尽くした点数
にしてやればよさそう。$i$を閉区間、$j$を開区間にするのは重複を避けるための小技だったりします。長さを$j-i$でとれるので便利だったりします。
漸化式は
dp[i][j]=\left\{
\begin{array}{ll}
max(dp[i][j-1]+a_{j-1} , dp[i+1][j]+a_{i})(先手番) \\
min(dp[i][j-1]-a_{j-1} , dp[i+1][j]-a_{i})(後手番)
\end{array}
\right.
サイズが1小さい区間からとってくるイメージですね!
図で表すと
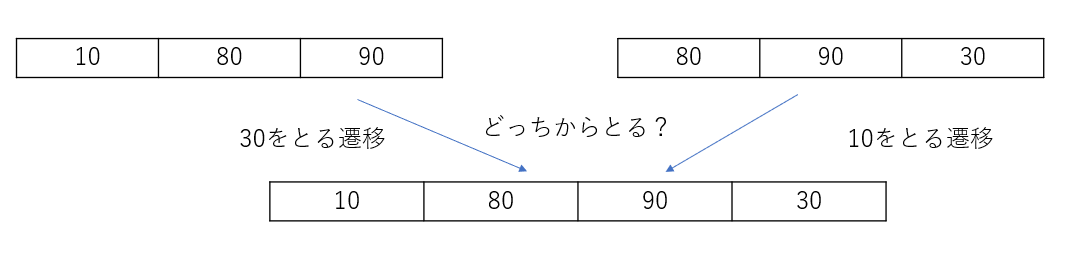
コード例
int main()
{
int n;
cin >> n;
V vec(n);
rep(i, n) cin >> vec[i];
VV dp(n + 1, V(n + 1)); //[i,j)の範囲 VV=vector<vector<int>>
for (int i = 1; i <= n; i++){ //長さ小さいほうから
for (int j = 0; j + i <= n; j++){//左,nを超えないように
int k = i + j; //右
if ((n - i) % 2 == 0){ //先手 遷移するイメージ
dp[j][k] = max(dp[j + 1][k] + vec[j], dp[j][k - 1] + vec[k - 1]);
}else{ //後手
dp[j][k] = min(dp[j + 1][k] - vec[j], dp[j][k - 1] - vec[k - 1]);
}
}
}
cout << dp[0][n] << endl;
}
計算量は$O(N^2)$です。
M問題-Candies
(https://atcoder.jp/contests/dp/tasks/dp_m)
ここらへんから、かなりしんどいです。
N人の子供にK個の飴を配るのですが、一人当たり上限があるようです。
そこで、このような状態を考えてみましょう。
dp[i][j]-i人目まで見てj個の飴を配る
漸化式を考えると
dp[i][j]=\sum_{k=max(0,j-a_i)}^{j}dp[i-1][k]
i番目の子にj-k個配ってます。
イメージとしてはこう!
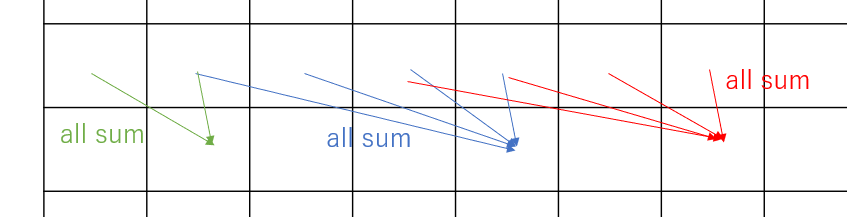
でもこれだと計算量が$O(NK^2)$になりますね…絶対間に合いません。
でも、この図を見て何かに気づきませんか?何回も区間を足し算する…そう!累積和です!
下処理としてi-1の行を足し上げてやることで計算量$O(NK)$に落とすことが可能です!
コード例
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
ll n, k;
cin >> n >> k;
V vec(n);
for (int i = 0; i < n; i++)cin >> vec[i];
VV dp(n + 1, V(k + 1));//dp配列です
for (int i = 0; i <= n; i++)dp[i][0] = 1;//0個配るのは1通りです
for(int i=0; i < n; i++){
V vec2(k + 1);//累積和用の配列です、名前もっとちゃんとしないといけないな…
vec2[0] = dp[i][0];
for (int j = 1; j <= k; j++)vec2[j] = dp[i][j] + vec2[j - 1];//累積和下処理です!
for (int j = 1;j<= k;j++){
if (j - vec[i] <= 0){
dp[i + 1][j] = vec2[j];//図の緑のようにはみだしちゃうやつがあるので注意です
dp[i + 1][j] %= MOD;
}else{
dp[i + 1][j] = vec2[j] - vec2[j - vec[i] - 1];
dp[i + 1][j] %= MOD;
}
}
}
cout << dp[n][k] << endl;
}
MODを取るのを忘れずに!
最後に
とりあえず、これでやっとEDPCの半分まで解説しました。
なんとZ問題まであるんですね。M問題でも四苦八苦しながら解いてるのに現実は厳しいですね。
Z問題まで解説できるように、これからも精進したいと思います。