あみだくじの偏りをR言語で調べる

あみだくじは有限本の横線では完全にランダムにならないということが知られている。このことを観察するために、統計処理のための言語であるR言語(https://www.r-project.org/) でシミュレーションを行ってみる。

まずはあみだくじのシミュレーターを作る。入力された縦線と横線の本数$n,m$に従ってランダムなあみだくじが作られる。開始位置は変数startによって与える（左端が1）。

ghostlegSimulation  <- function(start, verticalNum, horizontalNum)
{
    current <- start
    horizontalLines <- sample(1 : (verticalNum - 1), horizontalNum, replace = TRUE)
    for(i in 1 : horizontalNum) {
        nextLine <- horizontalLines[i]
        if(nextLine == current - 1) {
            current <- current - 1
        }
        else if(nextLine == current) {
            current <- current + 1
        }
    }
    return(current)
}

シミュレーターができたら、実際に何個もあみだくじを作って回してみる。あみだくじの個数numを入力に加えて、ヒストグラムを表示できるようにした。

simulations <- function(start, verticalNum, horizontalNum, num)
{
    goals <- c()
    for(i in 1 : num) {
        result <- ghostlegSimulation(start, verticalNum, horizontalNum)
        goals <- c(goals, result)
    }
    return(goals)
}

viewHistgram <- function(start, verticalNum, horizontalNum, num)
{
    result <- simulations(start, verticalNum, horizontalNum, num)
    histgram <- hist(result, breaks = 0 : verticalNum)
    return(histgram)
}

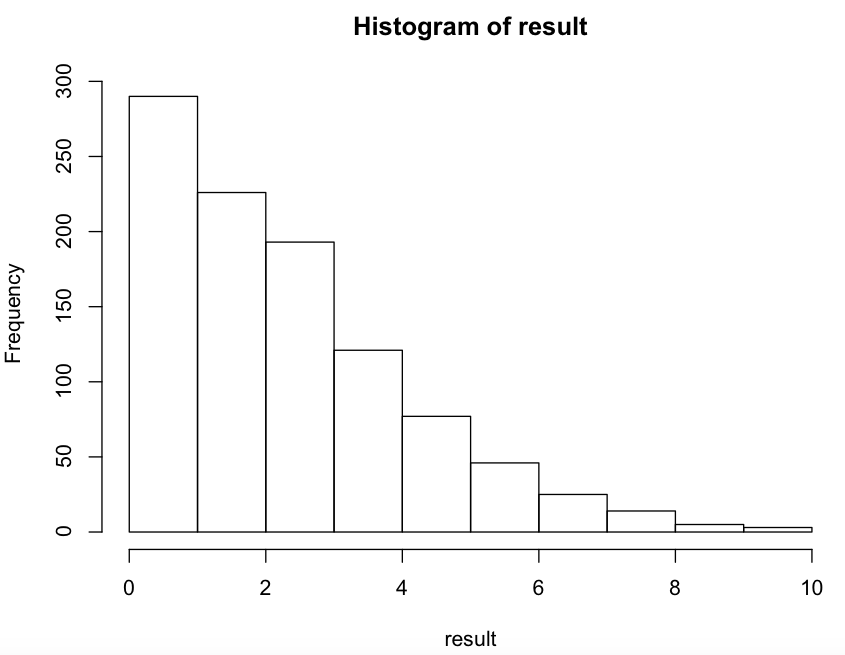
ひとまず、縦線10本、横線20本でどうなるかを見てみよう。

histgram <- viewHistgram(1, 10, 40, 1000)

こ　れ　は　ひ　ど　い
右端に至っては3つしか到達していなかった。しかしながら、40本も横線を引くのはけっこう大変である。普通に作れるレベルのあみだくじはひどく偏っていて、当たりから一番遠い場所を選ぶとほとんど当たらないということがわかる。

次に、どの程度の横線の本数があればそれなりにランダムだといえるかを考える。ここではピアソンの適合度検定を使う。

ピアソンの適合度基準 = \sum \frac{(理論度数-期待度数)^2}{期待度数}

これは自由度$n-1$のカイ二乗分布に従うということが知られている。まず、先程のデータに対して有意水準$\alpha=0.05$で検定を行ってみる。

testHistgram <- function(histgram, verticalNum)
{
    expected <- rep(1 / verticalNum, length = verticalNum)
    result <- chisq.test(x = histgram$counts, p = expected)
    return(result)
}

testHistgram(histgram, 40)

結果は以下のようになった。

Chi-squared test for given probabilities

data:  histgram$counts
X-squared = 911.48, df = 9, p-value < 2.2e-16

p-valueが0.05を上回っていれば帰無仮説は棄却できず、ランダムである可能性があるといえるのだが、2.2e-16未満というわけで、ほぼ0の数値が出ており全然だめである。

さてここからが本題だ。有意水準$\alpha=0.05$で検定を行って棄却されなくなるまで横線の本数を増やし続けるということを考える。

ghostlegTest <- function(start, verticalNum, horizontalNum, num)
{
    histgram <- viewHistgram(start, verticalNum, horizontalNum, num)
    result <- testHistgram(histgram, verticalNum)
    return(result)
}

goodNumber <- function(start, verticalNum, num, significanceLevel, initHorizontalNum)
{
    horizontalNum <- initHorizontalNum
    repeat {
        testResult <- ghostlegTest(start, verticalNum, horizontalNum, num)
        if(testResult$p.value > significanceLevel) {
            break
        }
        horizontalNum <- horizontalNum + 30
    }
    return(horizontalNum)
}

goodNumber(1, 10, 1000, 0.05, 40)

結果は280本。ヒストグラムは次のようになった。

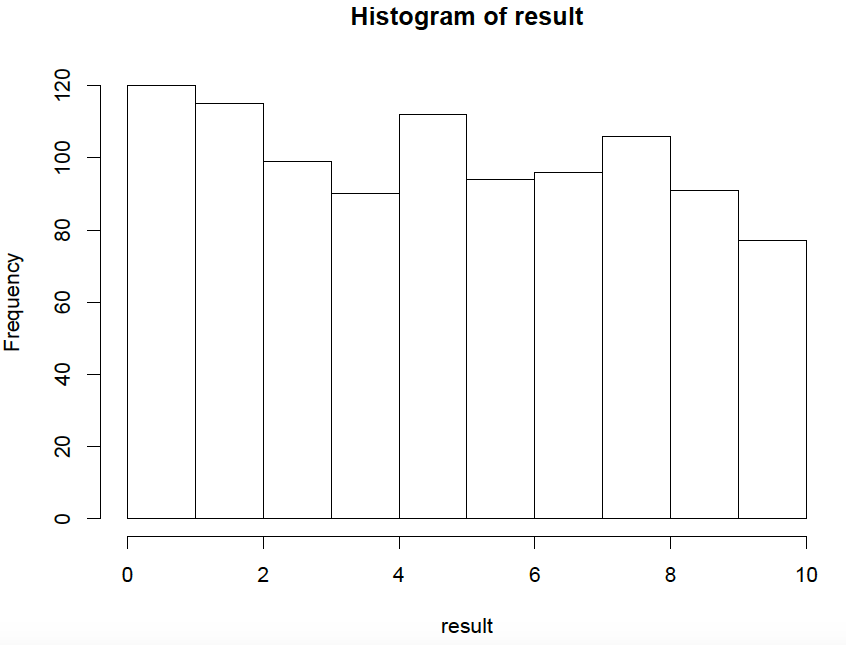
縦線10本に対して280本も横線を引いたのに、まだ若干左に偏っているように見える。抽選方法として、あみだくじがいかに不公平かということがよくわかった。

#####参考にした書籍