LoginSignup
30
30

More than 5 years have passed since last update.

@zakuroishikuro(zakuro)

CSSの3Dトランスフォームで正多面体を作る

Last updated at Posted at 2016-05-18

CSSの理解を深めるために立体図形を作成した。
何か間違ってたらごめんなさい。

正多面体とは

これら5つの立体のこと。これら以外には存在しない。

正四面体 正六面体 正八面体 正十二面体 正二十面体
120px-Tetrahedron-slowturn.gif 120px-Hexahedron-slowturn.gif 120px-Octahedron-slowturn.gif 120px-Dodecahedron-slowturn.gif 120px-Icosahedron-slowturn.gif

画像は 正多面体 - Wikipedia より。

全ての面が等しい正多角形で、全ての面で接する頂点の数が等しい。

※注： 十二面体、二十面体は完成しませんでした。 誰か作って

正六面体

120px-Hexahedron-slowturn.gif

いわゆる立方体。サイコロ。
なぜ正四面体から始めないのか？
正六面体が一番お手軽だからだ。

サンプル。
http://jsrun.it/zakuroishikuro/WKlN - jsdo.it

作成手順

色付け等の装飾要素を省き、正六面体を表示するための最低限のソースを書く。
上記のサンプルと異なり、枠線のみ描画される。

divを6枚用意し、一つのまとまりとするためにdivで包む。(obj)
消失点(perspective-origin)ごと移動可能とするため、さらにdivで包む。(base)
これだけでhtml側は完成。

cube.html
<div class="base">
  <div class="obj">
    <div class="left"></div>
    <div class="right"></div>

    <div class="top"></div>
    <div class="bottom" ></div>

    <div class="back"></div>
    <div class="front"></div>
  </div>
</div>

CSSで組み立てていく。
まず各面を3Dトランスフォームするための準備。

cube_common.css
div {
  height: 200px; width: 200px; /* divは全て200px * 200pxにする */
  position: absolute; /* 全て重ねる */
}

.base {
  perspective: 900px; /* z軸の原点(0)までの距離を設定 (画面の900px前に視点を移動) */
}

.obj {
  transform-style: preserve-3d; /* 子要素を立体的に表示 */
}

各面を組み立てていく。前面はいじる必要がない。

cube_polygon.css
.left { /* 左の面 */
  transform-origin: left; /* 原点を左の辺に置く */
  transform: rotateY(90deg); /* Y軸を90度回転 */
}

.right { /* 右の面 */
  transform-origin: right; /* 原点を右の辺に置く */
  transform: rotateY(-90deg); /* Y軸を-90度回転 */
}

.top { /* 上の面 */
  transform-origin: top; /* 原点を上の辺に置く */
  transform: rotateX(-90deg) /* X軸を-90度回転 */;
}

.bottom { /* 下の面 */
  transform-origin: bottom; /* 原点を下の辺に置く */
  transform: rotateX(90deg); /* X軸を90度回転 */
}

.back { /* 後ろの面 */
  transform: translateZ(-200px); /* 面を後ろに移動するだけ */
}

立体と分かるよう、枠線を表示し、回転させて完成。

cube_anim.css
.obj > div {
  box-sizing: border-box; /* 枠線が面からはみ出ないようにする */
  border: 10px dotted black;  /* 幅10ピクセルの点線 */
}

@keyframes spin{
  from {transform: rotateY(0turn)}
  to {transform: rotateY(1turn)} /* Y軸で360度回転 */
}

.obj {
  /* オブジェクトは奥に作成されているので、その真ん中(z軸-100px)を回す */
  transform-origin: 50% 50% -100px;
  animation: 10s spin linear infinite;
}

正六面体に必要なソースはこれだけ。

面は全て正方形なので、divをそのまま使える。
面と面の間の角(二面角)は90度なので、何も計算せずに作れる。
かんたん。

また、原点を移動せずにtranslateやposition: absoluteで面を移動してから回転させる方法もある。

正四面体

120px-Tetrahedron-slowturn.gif

サンプル。
http://jsrun.it/zakuroishikuro/SoHx - jsdo.it

正六面体では、面が正方形だったのでdivに色を塗るだけで作れた。
正四面体では、面が正三角形なのでSVGで描く。

SVGで正三角形を描く

<svg viewBox="0,0 2 2">
  <path d="M0,2 h2 l-1,-1.7320508075688772 Z" fill="black"/>
</svg>

これで1辺の長さが2の正三角形を描ける。
2px * 2pxと非常に小さいが、SVGは無限に拡大可能なので、CSSでサイズ指定してあげればいい。

簡単に説明すると、viewBoxで表示範囲の座標(0,0)と大きさ(2*2)を指定。
座標(0,2)から水平に長さ2の線を引き、その位置からX軸 $-1$, Y軸 $-\sqrt{3}$ の座標へ線を引いている。
高さが$\sqrt{3}$なのは三平方の定理による。

正四面体の二面角

灰色の正三角形が底面で、青色の正三角形との間にオレンジの直角三角形が挟まれている。
その左下の「？」が二面角。この角度が分かれば面をどれだけ傾ければよいか分かる。

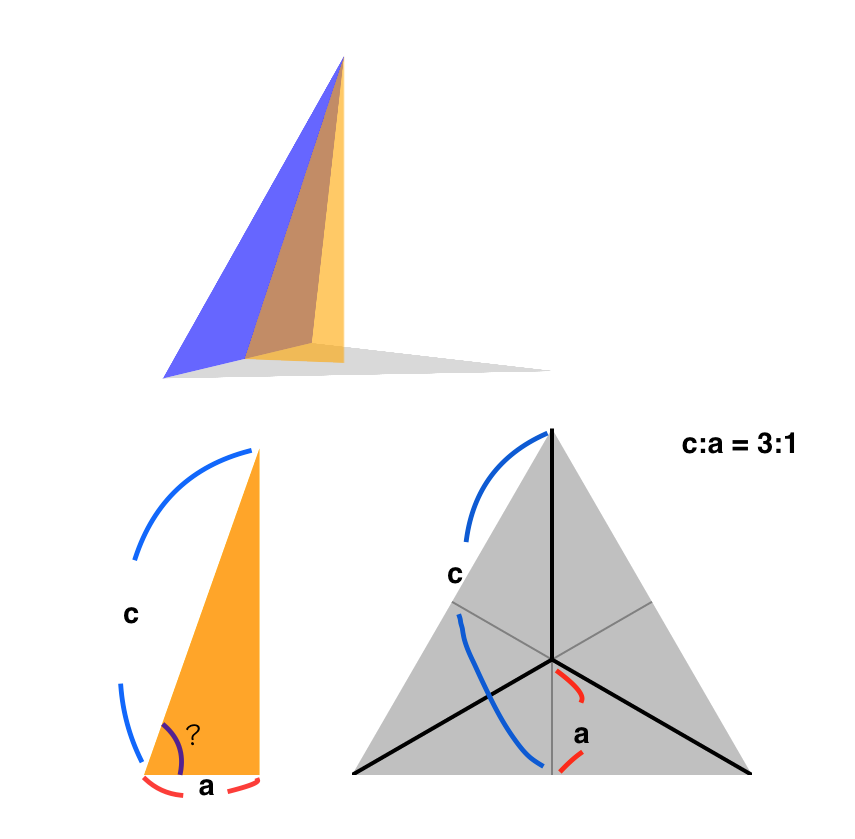
スクリーンショット 2016-05-17 21.17.04.png

http://jsrun.it/zakuroishikuro/IWai - jsdo.it

「？」の角度を求めるには逆三角関数を使う。
三角比の逆で、直角三角形の2辺の比から角度を計算できる。
「$\sin^{-1}$」のように書いて「アークサイン」等と読む。

右下は正四面体を上から見た図。
$a$の長さは、底辺からちょうど正三角形の重心まで。$a = c \div 3$
灰色は青色と合同なので、$c = $ 灰色の高さ。

$c = 3$として、「？」の角度を計算する。

\cos^{-1} \frac{1}{3} = 70.52877936550931...

「？」の角度は約70度であることが分かった。
ということは、90° - 約70°の 19.47122063449069° 傾ければいい。($\sin^{-1} \frac{1}{3}$でも可)

JavaScriptでは90 - Math.acos(1/3) * 180 / Math.PIのように計算できる。

作成手順

正三角形を表示する方法と二面角が分かったので、組み立てていく。
4枚の正三角形(SVG)を作る。SVGの色付けはCSSでも可能だが、今回はHTML側で行う。

reg_tetra.html
<div class="base">
  <div class="obj">
    <svg class="front" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="red"/></svg>
    <svg class="left" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="green"/></svg>
    <svg class="right" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="blue"/></svg>
    <svg class="bottom" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="silver"/></svg>
  </div>
</div>

CSS。ここは正六面体とだいたい同じ。
最初のルールのセレクタをdiv, svgとしたのと、不透明度(opacity)を追加した。

reg_tetra_common.css
div, svg {
  height: 200px; width: 200px; /* divは全て200px * 200pxにする */
  position: absolute; /* 全て重ねる */
}

.base {
  perspective: 900px; /* z軸の原点(0)までの距離を設定 (画面の900px前に視点を移動) */
}

.obj {
  transform-style: preserve-3d; /* 子要素を立体的に表示 */
}

.obj > svg {
  opacity: 0.6; /* 半透明にする */
}

面を傾けていく。
正三角形の一つの角は60°なので、Y軸は60°回す。

reg_tetra.css
.front { /* 前面 */
  transform-origin: bottom; /* 原点を底辺に移動し */
  transform: rotateX(19.47122063449069deg); /* X軸を約19°傾ける */
}

.left { /* 左の面 */
  transform-origin: bottom left; /* 原点を左下に移動し */
  transform: rotateY(60deg) rotateX(-19.47122063449069deg); /* Y軸を60°回し、X軸を約-19°傾ける */
}

.right { /* 右の面 */
  transform-origin: bottom right; /* 原点を右下に移動し */
  transform: rotateY(-60deg) rotateX(-19.47122063449069deg); /* Y軸を-60°回し、X軸を約-19°傾ける */
}

.bottom { /* 底面 */
  transform-origin: bottom; /* 原点を底辺に移動し */
  transform: rotateX(90deg); /* X軸を90度回す */
}

アニメーション。z軸の原点の計算がややめんどい。

reg_tetra_anim.css
@keyframes spin{
  from {transform: rotateY(0turn)}
  to {transform: rotateY(1turn)}
}
.obj {
  /* オブジェクトは奥に作成されているので、その真ん中(z軸-約57px)を回す */
  transform-origin: 50% 50% calc(-200px / 2 * (1.7320508075688772 / 3));
  animation: 10s spin linear infinite;
}

正八面体

120px-Octahedron-slowturn.gif

サンプル。
http://jsrun.it/zakuroishikuro/0dKl - jsdo.it

いわゆるラミエル。
面は正三角形なので、正四面体から流用できる。

正八面体の二面角

上半分のビラミッド型の図形を考える。
このピラミッド型は4枚の正三角形で構成されており、上から見ると正方形になっている。
正三角形の1辺の長さ = 正方形の1辺の長さ。

正四面体の時に考えた、面に挟まれたオレンジ三角形を考える。

正三角形の1辺の長さを2とすると、三平方の定理より高さは$\sqrt{3}$。これがオレンジ三角形の斜辺。
正方形の1辺の長さも2なので中心までは長さ1。これがオレンジ三角形の底辺。
2辺の比が分かったので角度を計算できる。

\cos^{-1}\frac{1}{\sqrt{3}} = 54.735610317245346...

$90° - 約54°$で 35.264389682754654°傾ければいい。
(ちなみに二面角は2倍の109.47122063449069...。)

作成手順

正四面体のsvgを4枚増やしたような感じ。

<div class="base">
  <div class="obj">
    <svg class="front" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="red"/></svg>
    <svg class="back" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="silver"/></svg>
    <svg class="left" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="green"/></svg>
    <svg class="right" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="blue"/></svg>

    <svg class="bottom front" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="silver"/></svg>
    <svg class="bottom back" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="red"/></svg>
    <svg class="bottom left" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="blue"/></svg>
    <svg class="bottom right" viewBox="0,0 2 2"><path d="M0,2 h2 l-1,-1.7320508075688772" fill="green"/></svg>
  </div>
</div>

ここは正四面体と全く同じ。

reg_hexa_common.css
div, svg {
  height: 200px; width: 200px; /* divは全て200px * 200pxにする */
  position: absolute; /* 全て重ねる */
}

.base {
  perspective: 900px; /* z軸の原点(0)までの距離を設定 (画面の900px前に視点を移動) */
}

.obj {
  transform-style: preserve-3d; /* 子要素を立体的に表示 */
}

.obj > svg {
  opacity: 0.6; /* 半透明にする */
}

傾ける。枚数増えたからやたらめんどくさい。

reg_hexa.css
.front {
  transform-origin: bottom;
  transform: rotateX(35.26438968275467deg);
}

.back {
  transform-origin: bottom;
  transform: translateZ(-200px) rotateX(-35.26438968275467deg);
}

.left {
  transform-origin: bottom left;
  transform: rotateY(90deg) rotateX(-35.26438968275467deg);
}

.right {
  transform-origin: bottom right;
  transform: rotateY(-90deg) rotateX(-35.26438968275467deg);
}

.bottom.front {
  transform-origin: bottom;
  transform: rotateX(144.73561031724535deg); /* 180° - 約35° */
}

.bottom.back {
  transform-origin: bottom;
  transform: translateZ(-200px) rotateX(-144.73561031724535deg);
}

.bottom.left {
  transform-origin: bottom left;
  transform: rotateY(90deg) rotateX(-144.73561031724535deg);
}

.bottom.right {
  transform-origin: bottom right;
  transform: rotateY(-90deg) rotateX(-144.73561031724535deg);
}

アニメーション。

reg_hexa_anim.css
@keyframes spin{
  from {transform: rotateY(0turn)}
  to {transform: rotateY(1turn)}
}
.obj {
  /* オブジェクトは奥に作成されているので、その真ん中(z軸-100px)を回す */
  transform-origin: 50% 50% 100px;
  animation: 10s spin linear infinite;
}

正四面体よりもだいぶ雑になったけどおしまい。
上半分と下半分で作り分けたほうがいいんだと思う。

正十二面体

120px-Dodecahedron-slowturn.gif

ここから急に難度が跳ね上がる。
枚数が増えてめんどくささも格段に増す。
新しく正五角形のSVGも書かなければいけない。

いままでの図形はY軸と底辺を回すだけで作れた。
ここからは、回す軸の座標と角度も指定しなければならない。
完全に別ゲー。

正五角形のSVGを描く

正n角形を描く方法を考える。

正多角形の全ての頂点は、一つの円の円周上にある。
ということは、円周上に均等にnつの点を打って繋げばいい。
円周を3で割って繋げば正三角形ができる。

Canvasでやってみるとこう。
http://jsrun.it/zakuroishikuro/G3dQ - jsdo.it

draw_reglar_polygon.js
  function draw(n){
    reset_canvas(); // キャンバスの内容を消去する関数

    // ctxはcanvasのコンテキスト
    // rは円の半径(ctx.canvas.width / 2)
    ctx.beginPath();
    for (var i = 0; i < n; i++){
      var rad = Math.PI * 2 / n * i;
      var x = Math.cos(rad) * r;
      var y = Math.sin(rad) * r;
      ctx.lineTo(x, y);
    }
    ctx.closePath();
    ctx.stroke();
  }

よく分かんない人は『数学ガールの秘密ノート 丸い三角関数』を読むと幸せになれる。
(この方法が直接的に書かれているわけではないけど。)

もろもろ省略して正五角形のSVGはこんなん。

<svg viewBox="0,0 2 2">
  <path d="
    M1,0
    L1.9510565162951536,0.6909830056250525
    L1.5877852522924731,1.8090169943749475
    L0.412214747707527,1.8090169943749475
    L0.04894348370484636,0.6909830056250528
    Z" fill="silver"/>
</svg>

面を傾ける方法

今までは 底辺を軸に 面を傾けるだけで何とかなった。
今度は五角形の 各辺を軸に 傾けなければいけない。

イメージはこんなん。
300px * 300pxの矩形の左下で、縦100px * 横200pxの直角三角形が斜辺を軸に回っている。
http://jsrun.it/zakuroishikuro/YqjU - jsdo.it

辺を軸に回転させるには、原点を辺の中心に移動し、rotate3dでその辺に沿ったベクトルを指定する。
上のイメージでは以下のようにして回転させている。

@keyframes spin{
  /* X軸方向に2、Y軸方向に1、Z軸方向に0のベクトルを軸にして360度回転させる */
  from {transform: rotate3d(2, 1, 0, 0deg)}
  to {transform: rotate3d(2, 1, 0, 360deg)}
}

svg {
  /* 原点を移動。矩形は300px * 300pxで、X軸はその半分、Y軸は3/4 */
  transform-origin: calc(300px / 2) calc(300px / 4 * 3);

  animation: spin 3s linear infinite;
}

お詫び

私の園卒の脳と集中力ではここまでが限界でした。(動物園)
心よりお詫びいたします。

http://jsrun.it/zakuroishikuro/cOai - jsdo.it

せっかく途中まで書いたので、投稿します。
申し訳ございませんでした。

あ、Wikipediaによると二面角は$\cos^{-1}\frac{-1}{\sqrt{5}}$で約116°らしいです。

正二十体

120px-Icosahedron-slowturn.gif

頑張れ。

あとがき

間違ってもCSSでガンダムを建造しようとか考えないこと。
複雑な3Dを扱いたい場合はJavaScriptとThree.jsとかのライブラリ使ってやること。

あとCSSの角度の単位は度数(deg)だけでなくラジアン(rad)も使える。
Math.atanなどの逆三角関数はラジアンを返すけど、わざわざ度数に変換しなくてもいい。
ちなみに1回転(turn)や400°を1回転とする(grad)も使える。

あとあとここでは面の裏表は考慮していないのでbackface-visibilityをhiddenにすると表示できません。

参考リンク

MDN

Wikipedia

日本語のページは絶望的に情報が少ないので英語のページを見たほうがいい。

30
30
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
30
30