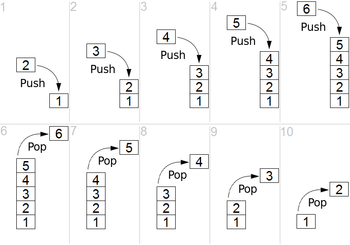
スタック
- Last In, First Outなデータ構造
- 許される操作は
PushとPopとClearだけ
逆ポーランド記法
逆ポーランド記法(ぎゃくポーランドきほう、英語: Reverse Polish Notation, RPN)は、数式やプログラムの記法の一種。演算子を被演算子の後にすることから、後置記法 (Postfix Notation) とも言う。
スタックを配列で実現する
- スタックを宣言するときに長さを与える必要がある
package main
import (
"fmt"
"os"
)
const LENGTH = 10
type Stack struct {
arr []int
sp int
}
func (s *Stack) Clear() {
s.sp = -1
}
func (s *Stack) Push(val int) {
if s.sp >= len(s.arr) {
fmt.Printf("ERROR: stack overflow\n")
os.Exit(1)
}
s.sp += 1 // スタックポインタを上げてから
s.arr[s.sp] = val // プッシュ
}
func (s *Stack) Pop() int {
if s.sp <= -1 {
fmt.Printf("ERROR: stack underflow\n")
os.Exit(1)
}
ret := s.arr[s.sp] // ポップしてから
s.sp -= 1 // スタックポインタを下げる
return ret
}
func NewStack(length int) *Stack {
if length <= 0 {
fmt.Println("ERROR: length of array should be more than zero")
os.Exit(1)
}
return &Stack{
arr: make([]int, length),
sp: -1,
}
}
func main() {
input := make([]int, LENGTH)
for i, _ := range input {
input[i] = i
}
fmt.Println("Input: ", input)
s := NewStack(LENGTH)
for ele := range input {
s.Push(ele)
}
for i := 0; i < LENGTH; i++ {
fmt.Println("Pop: ", s.Pop())
}
}
スタックをリストで実現する
- スタックを宣言するときに長さが不要
package main
import (
"fmt"
"os"
)
type Cell struct {
val int
prev *Cell
next *Cell
}
type Stack struct {
sp *Cell
}
func (s *Stack) Clear() {
s.sp = nil
}
func (s *Stack) Pop() int {
if s.sp == nil {
fmt.Println("ERROR: no value in stack")
os.Exit(1)
}
ret := s.sp.val
s.sp = s.sp.prev
return ret
}
func (s *Stack) Push(val int) {
fmt.Println("PUSH: ", val)
c := NewCell(val)
if s.sp == nil {
s.sp = c
return
}
s.sp.next = c
c.prev = s.sp
s.sp = c
}
func NewCell(val int) *Cell {
return &Cell{val: val, prev: nil, next: nil}
}
func NewStack() *Stack {
return &Stack{sp: nil}
}
func main() {
s := NewStack()
s.Push(3)
s.Push(4)
s.Push(5)
fmt.Println("Pop: ", s.Pop())
fmt.Println("Pop: ", s.Pop())
fmt.Println("Pop: ", s.Pop())
}
逆ポーランド記法で書かれた式をスタックを用いて評価する
package main
import (
"fmt"
"os"
"strconv"
"strings"
)
type Stack struct {
arr []int
sp int
}
func (s *Stack) Clear() {
s.sp = -1
}
func (s *Stack) Push(val int) {
if s.sp >= len(s.arr) {
fmt.Printf("ERROR: stack overflow\n")
os.Exit(1)
}
s.sp += 1 // スタックポインタを上げてから
s.arr[s.sp] = val // プッシュ
}
func (s *Stack) Pop() int {
if s.sp <= -1 {
fmt.Printf("ERROR: stack underflow\n")
os.Exit(1)
}
ret := s.arr[s.sp] // ポップしてから
s.sp -= 1 // スタックポインタを下げる
return ret
}
func NewStack(length int) *Stack {
if length <= 0 {
fmt.Println("ERROR: length of array should be more than zero")
os.Exit(1)
}
return &Stack{
arr: make([]int, length),
sp: -1,
}
}
func main() {
target := "2 1 + 3 *"
input := strings.Split(target, " ")
s := NewStack(len(input) + 1)
for _, ele := range input {
switch ele {
case "+":
right := s.Pop()
left := s.Pop()
s.Push(left + right)
case "-":
right := s.Pop()
left := s.Pop()
s.Push(left - right)
case "*":
right := s.Pop()
left := s.Pop()
s.Push(left * right)
case "/":
right := s.Pop()
left := s.Pop()
s.Push(left / right)
default:
s.Push(atoi(ele))
}
}
fmt.Println(target, " = ", s.Pop())
}
func atoi(a string) int {
ret, _ := strconv.Atoi(a)
return ret
}
ops = {
"+": (lambda a, b: a + b),
"-": (lambda a, b: a - b),
"*": (lambda a, b: a * b),
"/": (lambda a, b: a / b)
}
def eval(expression):
tokens = expression.split()
stack = []
for token in tokens:
if token in ops:
arg2 = stack.pop()
arg1 = stack.pop()
result = ops[token](arg1, arg2)
stack.append(result)
else:
stack.append(int(token))
return stack.pop()
print(eval("1 2 + "))
print(eval("990 1 2 + *"))
print(eval("1000 990 1 2 + * +"))
暇なときに普通の式を逆ポーランド記法にコンパイルするプログラムを書く。