コンピューターはどのように情報を処理しているのか? その原理の片鱗に触れてみたいと思います。
要約
以下を理解したいなと。
- なぜコンピュータの世界は0と1なのか?
- それはスイッチOn(1)/Off(0)の組み合わせで情報を処理しているから
- CPUは無数のスイッチの塊といえる
- コンピュータの計算は足し算が基本
- 足し算ができれば引き算や他の計算もできる
(半)加算器を作成してみる
コンピューターの世界は0と1(スイッチのOn, Off)。
で、足し算(加算)が基本。
では、スイッチのOn,Offだけでどのように計算(加算)するのか見てみる。
もっともシンプルな2進数、1桁(1bitどうし)の加算を考えてみます。
計算パータンを以下の通り。
- 0 + 0 = 0
- 1 + 0 = 1
- 0 + 1 = 1
- 1 + 1 = 10(桁上がり)
これらをスイッチのOn, Offで実装する(表現する)。
どう実装するか?
これらの処理を物理的に実装できればいいのですが、手間がかかるのでシミレータを利用してみたいと思います。
シミュレータはいくつか存在しますが、Web上で簡単に論理回路が試せるSimcirjsというのを利用してみます。
そもそも論理回路って何?って人はこちらをどうそ。
実装内容
加算器の実現方法にいくつかパターンがありますが、ここではWikipediaの図を利用させてもらうことにします。
AND, OR, NOTの比較的簡単な概念の論理ゲートのみで実装可能なパターンです。

Wikipediaから参照。
Sは答え(Sum), Cは繰り上げ(Carry)の意味。
Simcirjsによる実装
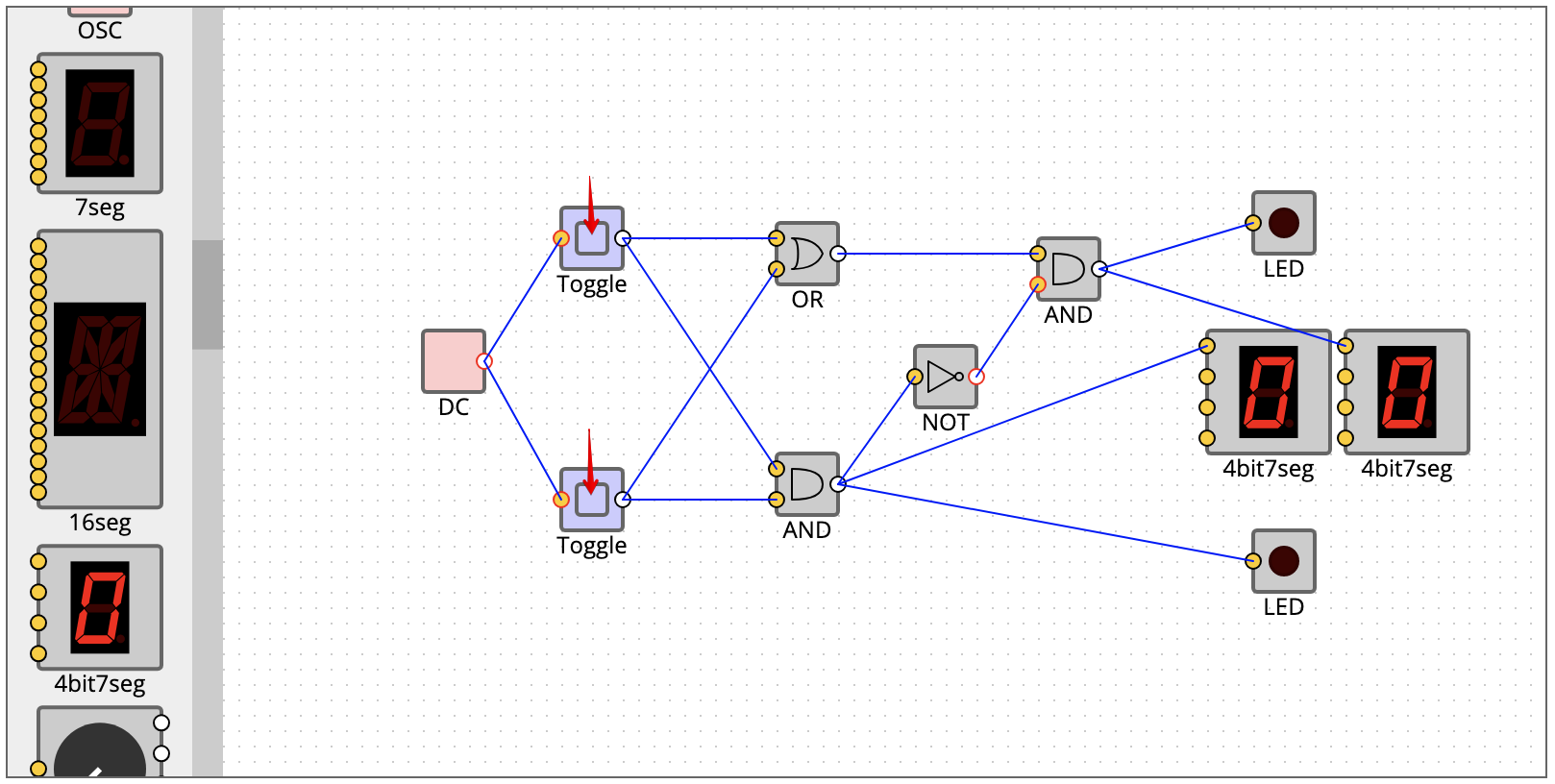
上記の回路図を実装するおおよそ下記のような感じになります。
- 実回路なので[DC]で電源確保
- Toggleスイッチで回路のOn, Off
- 計算結果が回路に電源が流れるならOn(1)でLED点灯。電気が流れないならOff(0)でLED消灯。

上記ではToggleが両方共OFF(LED両方とも消灯)の状態です。
見た目計算機ぽくしてみる
LEDが点灯するだけだと味気ないので、スイッチOnの再に[1]と表示するインジケータを利用してみます。
右が1桁目、左が2桁目となります。では、計算してみましょう。

0 + 0 (Off, Off)
この結果は上記と同じですね。両方のToggleスイッチがOffの状態です。
OnにするとToggleの中の□の色が濃くなります。
計算結果は0(0)ですね。
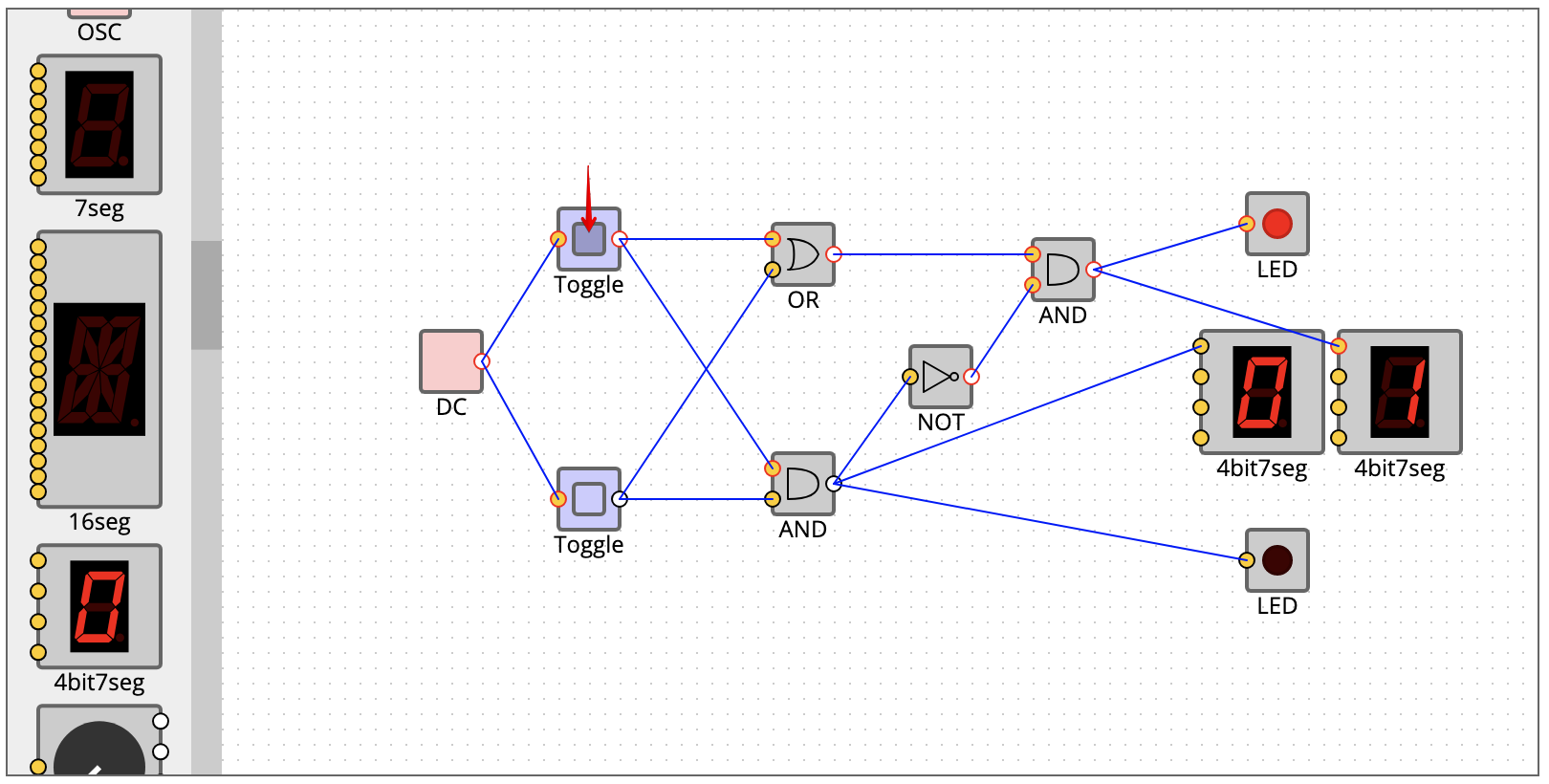
1 + 0 (On, Off)
次に1 + 1。で、結果はもちろん1。
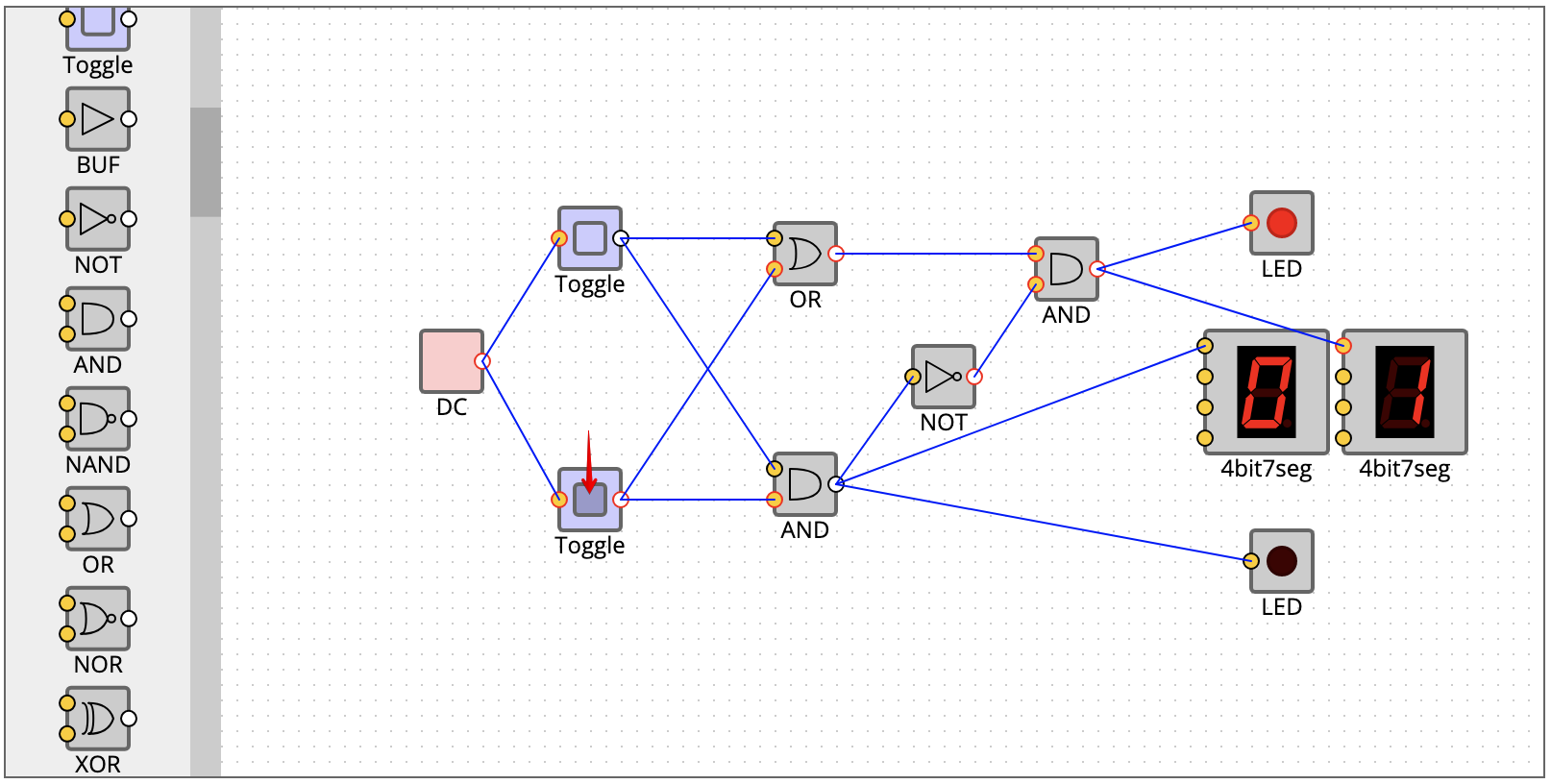
0 + 1 (Off, On)
次に0 + 1。結果は1。
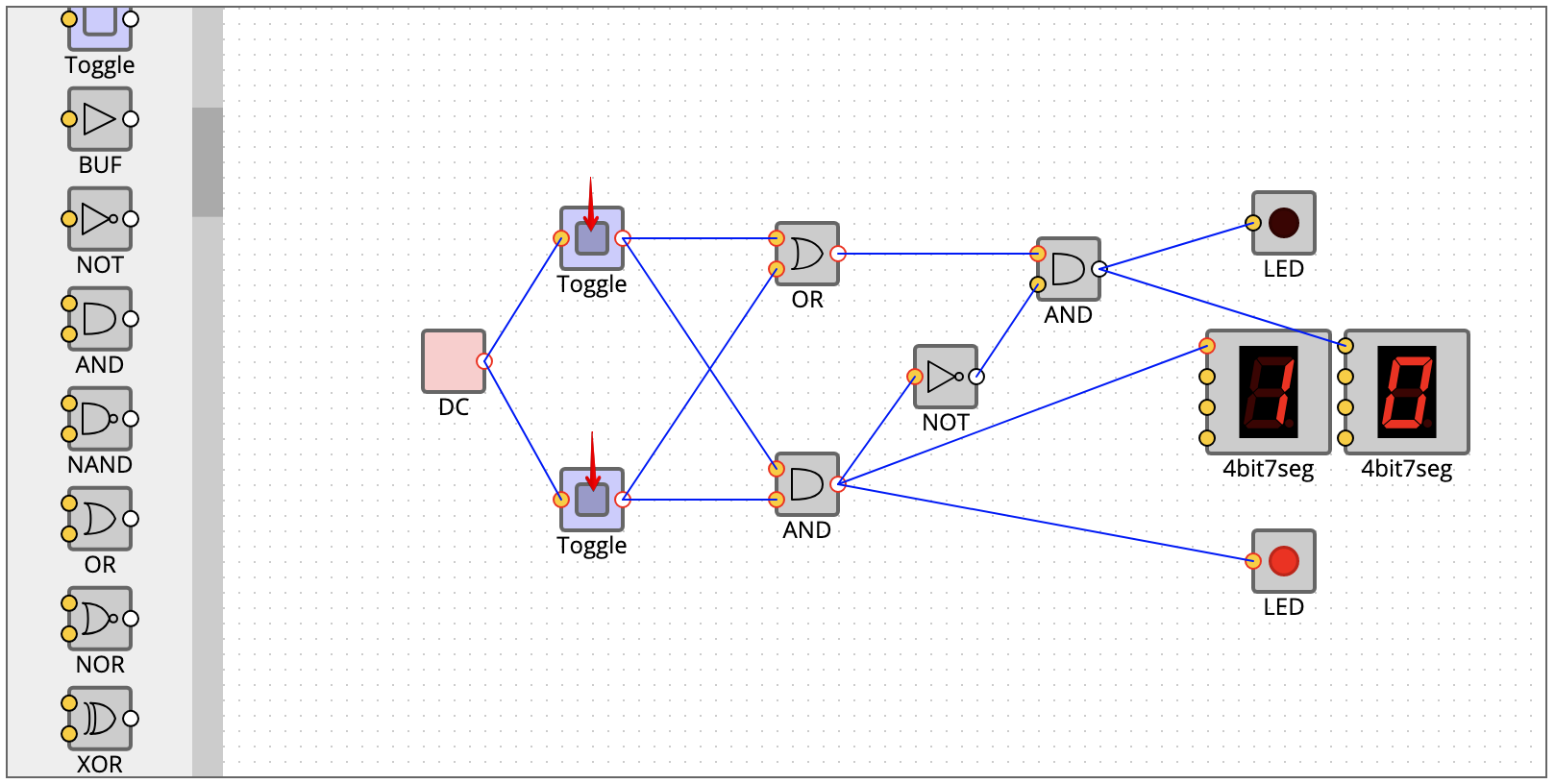
1 + 1 (On, On) 桁上り
最後に1 + 1。結果は10(2)。
これで、
- 0 + 0 = 0
- 1 + 0 = 1
- 0 + 1 = 1
- 1 + 1 = 10
が表現できました。
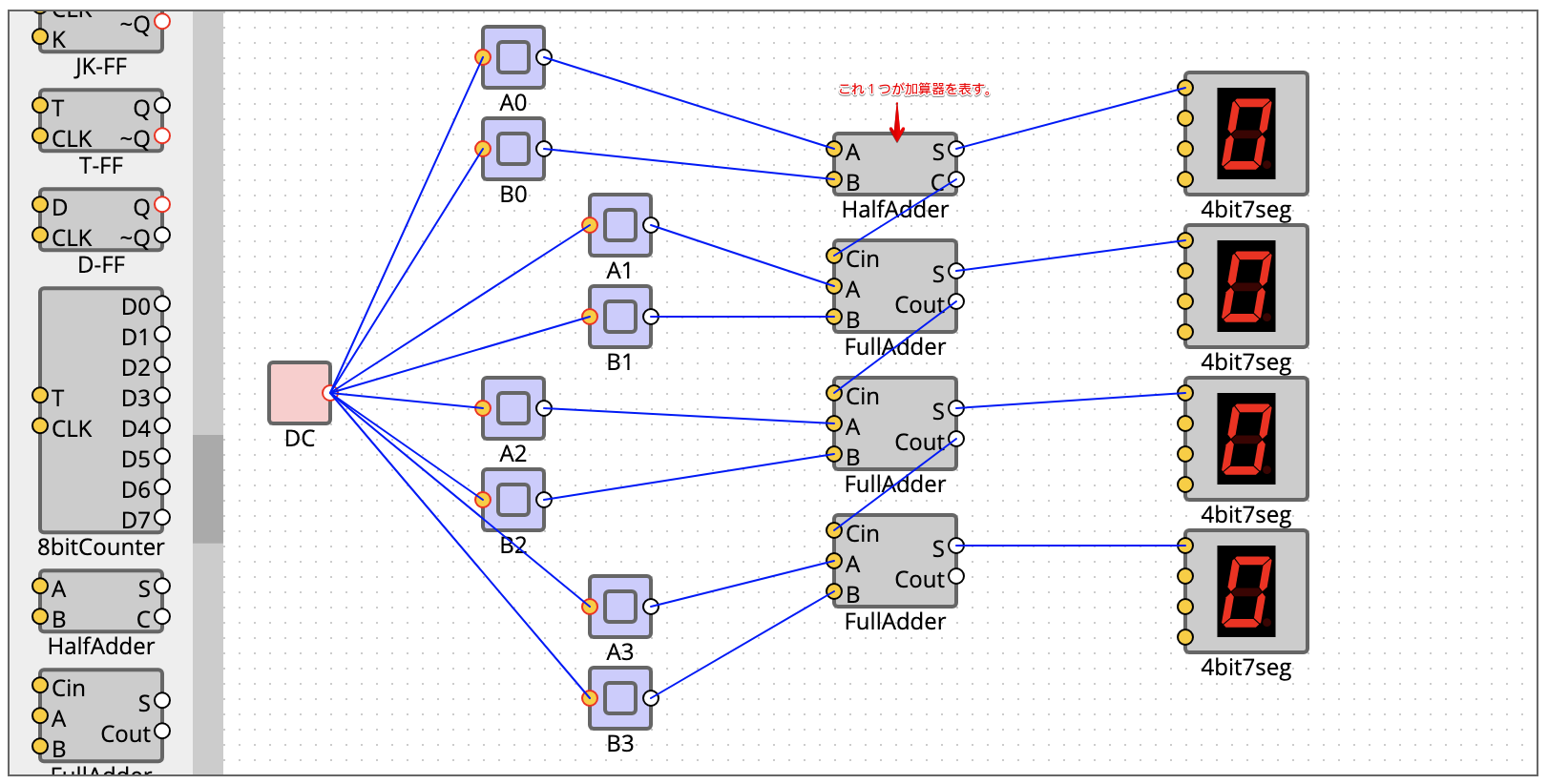
計算できる桁数を増やす
ここでは詳細は割愛しますが、加算器を組み合わせることで計算できるビット数を増やすことができます。
上記は4bit加算器の例。アイコンをクリックすると中身の回路が見えます(ここでの加算器はXORを利用したものになっている)。
(足し算で)減算してみる
加算器回路により足し算はできるようになりました。では、引き算はどうでしょう。
足し算ができれば、引き算はできるので問題ありません。
補数による減算
足し算で引き算するためには補数を利用します。
補数とは「ある数字nに対して、それを足せば桁上りする数字」のことです。
補数を利用することで引き算を足し算に変換することができます。
例えば、10進数において、3の補数は7です。6の補数は4です。つまり、足したら10(桁があがる)になる数字です。
ここで、
9 - 4
の引き算を考えてみます。4の補数は6ですが、それを利用して一旦、
9 + 6
の計算をします。答えは15です。その15の10の桁を無視します。すると5となります。これは9-4の答えです。
そもそも補数の計算に引き算が必要じゃないの?
感のいい人は気づいたかもしれませんが、そもそも補数を求めるのに、引き算が必要です。上記の場合だと、4の補数6を求めるには、
10 - 4 = 6
という計算が必要です。。。
幸いなことに、2進数における補数の計算は「機械的」に行うことが可能です。
例えば、101(5)の補数は、011となりますが(足すと1000となる数)、これは、101のビットを反転させ(010)たものに1を足すことで求められます。
このように2進数における補数は機械的(電気的)に簡単に求めることができます。