ついにイントロダクションが終わり、具体的な推薦システムの話に移ります。
はじめてTeXで数式を書いたので時間がかかりました…
前回分はこちら↓↓
http://qiita.com/ru_pe129/items/715753d4da383b98f5d2
Chapter 2 Data Mining Methods for Recommender Systems
本章ではRSにおける主なデータマイニングのテクニックの外観が示されています。
2.1 Introduction
RSはHCI(Human Computer Integration)やIR(Information Retrieval)などの手法を用いることが多いが、いずれも DM(Data Mining) をコアにした技術である。DMは主に3つのステップによって成り立つ。
- データの前処理
- 分析
- 解釈
2.2 Data Preprocessing
データは object(物、対象) と attribute(属性) の集合であると仮定する。objectはレコード、アイテム、点、サンプル、観察結果、例などと言い換えることができ、attributeは変数、分野、特徴、特性と言い換えることが出来る。実際に用いるデータには前処理が必要である。例えば、不要なデータやノイズを取り除いたり、分析可能な形式に変換したりすることが前処理に当たる。
2.2.1 Similarity Measures
強調フィルタリングには2.3.1で述べる kNN という分類手法が好んで用いられる。kNNでは、類似度や距離といった指標をどう定義するかが重要となる。もっとも一般的なものは ユークリッド距離 というもので、
d(x,y) = \sqrt{\sum_{k=1}^n (x_k-y_k)^{2}}
また、ユークリッド距離を一般化したもので ミンコフスキー距離 というものがある。
d(x,y) = (\sum_{k=1}^n |x_k-y_k|^{r})^{\frac{1}{r}}
ミンコフスキー距離においてr=1としたとき、これをマンハッタン距離と呼ぶ。r=1のとき、距離は各成分の差の絶対値を足し合わせたものになる。つまり、マンハッタンのような街でカクカク進んでいく時の距離を想像するとわかりやすい(日本人なら碁盤の目と言った方がわかりやすいでしょうか。) r=∞のときは成分の差の絶対値がもっとも大きい成分だけが残る。
マハラノビス距離 は以下の式で定義される。
d(x,y) = \sqrt{(x-y)\mathbf{\sigma^{-1}}(x-y)^{T} }
ここで、σはxとyの分散共分散行列とする。
コサイン類似度 は以下の式で定義される。
cos(\vec{x},\vec{y}) = \frac{\vec{x}\cdot\vec{y}}{|\vec{x}||\vec{y}|}
ピアソン相関係数は以下の式によって定義される。
Pearson(x,y) = \frac{\sum{(x,y)}}{\sigma_{x}\times\sigma_{y}}
ここで、分子はxとyの共分散、分母はxとyそれぞれの分散の積であるとする。
RSではコサイン類似度が用いられることが多い。ある研究結果では、RSでコサイン類似度を用いた場合が一番よい結果を得たという。しかし、ある研究ではRSの効果は類似度の計算方法に影響を受けないと言う。
次にアイテムがバイナリデータの時に用いる類似度指標を紹介する。SMC(Simple Matching coefficient)やJaccard coefficientのほかに、Extended Jaccard coefficient(連続値を用いる場合?)などがある。式は面倒くさいので省略。SMCは二つのアイテムで値が一致している要素の割合を求める。Jaccard coefficientは二つのアイテムの積集合を和集合で割ったもの。Extended Jaccard coefficientは二つのアイテムの内積をアイテムの差の絶対値の二乗で割ったもの。
2.2.2 Sampling
サンプリングはDMで大量のデータのサブセットを取得する上でメインとなる手法であり、データの前処理と解釈の二つのステップで用いられる。大量のデータすべてを解析することは非常にコストがかかるため、 サンプリングを行って解析対称を減らす ことを目的としている。また、サンプリングは訓練データとテストデータを作成する際にも用いられる。訓練データによってパラメーターやアルゴリズムを設定し、テストデータ(つまり、まだ使用していないデータ)を用いて調整の良し悪しを確かめる。
サンプリングで重要なことは、サンプリングによって取得したアイテムの集合が元のデータの特徴を持っていることである。もっとも一般的なサンプリングはランダムサンプリングであるが、ランダムサンプリングにも二種類ある。一つは一度選択したアイテムを次の選択対象から外すもの、二つ目は一度選択したアイテムを次の選択でも選択対象とするものである。訓練データとテストデータを得る場合には前者が用いられることが多い。割合としては訓練:テスト=80:20がもっとも一般的である。
サンプリングにはサンプリングで取得した集合の特徴に特化してしまうという問題点がある。つまり、サンプリングで取得した集合というのはデータ全体の特徴を表すものではなく、偏りがあることも十分に考えられるということである。この問題を解決するために、一般的にはサンプリングは複数回行われ、その平均的な結果を用いてモデルを作成する。この過程を cross-validation という。
- n-Fold cross validation
データをn分割し、1個をテストデータ、のこりのn-1個を訓練データとして扱い、訓練とテストをn回繰り返す。 - leave one out approach(LOO)
n-Fold cross valiationの特殊なケースで、n=アイテムの数として訓練とテストを繰り返す。
RSの基本的なアプローチとしてユーザーからのフィードバックのサンプリングを行う。しかし、サンプリングには偏りが書ずることも忘れてはならない。例えば、ユーザーのアイテムに対する評価は比較的新しいのものを対象とする。なぜなら、将来ユーザーが好むものを推薦するのに非常に古いデータをRSに用いるのは非効率だからである。
2.2.3 Reducing Dimentionality
RSで扱うデータは非常に多次元でスパース(まばらな、密度が低い)であることが多い。ここで問題となるのが 次元の呪い(Curse of Dimentionality) である。点と点の間の密度や距離といったクラスタリングで重要となる指標が多次元においては効果が小さくなることを次元の呪いという。そこで次元圧縮が必要となる。
2.2.3.1 Principal Component Analysis
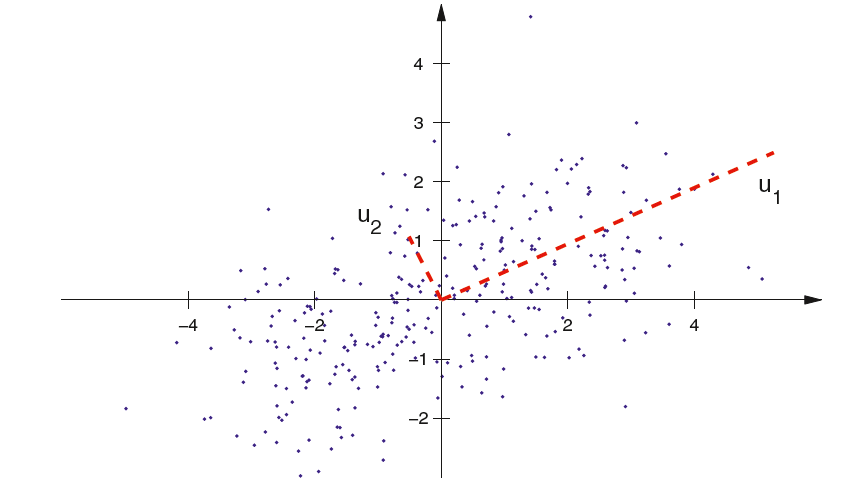
PCA(Principal Component Analysis)は多次元データからパターンを見つける古くから使われている統計手法である。簡単にまとめると、各次元の線型結合によって新たな次元を設け、分散が大きくなる場合のみを残して分散が小さくなる場合を無視するというものである。分散が大きいということは多くの情報を保存しているみなすことができ、逆に分散が小さければ情報を保存できていないとみなすことができるからである。以下にイメージとなる式を示す。
X_{n\times{m’}} = X_{n\times{m}}W'm\times{m'}
X'はXの情報をもっとも多く保存しているn×mデータを表しており、m-m'の次元圧縮に成功している。
主成分分析はパワフルな手法ではあるが、データがある程度線形である必要がある。(非線形に対応したものも提案されているらしいが…)また、元のデータがガウス分布にしたがっているという前提も必要となる。つまり、主成分分析のモデルを作った際に使用したデータに偏りがあれば作ったモデルは役に立つ保証はないということである。
PCAに関して追記
上記の説明だと意味不明なので補足しておく(自分の能力のせい)。以下のスライドが非常にわかりやすかった。
http://www.slideshare.net/sanoche16/tokyor31-22291701?from_search=2
現在トレンドとしてはSVDやNon-Negative Matrix Factoriationが好まれているようである。
2.2.3.2 Singular Value Decomposition
SVD(Singular Value Decomposition)を紹介する。日本語では特異値分解という。
今回はここまでにします。
SVDやPCAの理解がかなり曖昧なのでもうちょっとかっちりやってからSVDの話を書きたいと思います。(IIRや授業でやったはずなのに…)