適応型ハフマンエンコード実装

適応型ハフマンを実装したくて調べてたら意外といい情報が見つけられなかったので、今回はよくわからなかったところとc++での実装までを雑記していきます。

適応型ハフマンとは

軽くおさらいとして、ハフマン符号とは可逆圧縮が可能な符号です。wikipedia
データ全体の各文字の出現数に応じて出現頻度の高い文字ほど短い符号を割り当てて圧縮します。
例えばABABABACという文字列をハフマン符号化すると、Aが4文字、Bが3文字、Cが1文字なのでそれぞれに以下のようにビット列を割り当てて

	A	B	C
バイナリ	01000001	01000010	01000011
ハフマン	0	10	11

文字列全体としては010010010011の12ビットとなります。元が64bitなので約19%ほどに圧縮されました。実際には復号のためにこれに符号表も付加します。

普通のハフマンはいったんデータ全体の文字数をカウントしてから各符号長を決め2パス目で実際に符号化する2パスエンコードになりますが、適応型ハフマンは1パスで符号の決定と符号化を行います。そのためストリーミング処理に向いており、巨大なファイルの圧縮などにも適用しやすいです。

今回はこの符号の決定アルゴリズムであるVitterアルゴリズムが分かりにくかったのでその解説を実装も交えてできるだけ平易に書いていこうと思います。

Vitterアルゴリズム

ハフマン符号を決定する際は静的ハフマンでもハフマン木というバイナリツリーを構築することで適した符号を割り当てます。適応型ハフマンでもハフマン木を構築しますが、1文字入力される度にツリーを更新してその時点での符号を出力していきます。
Vitterアルゴリズムではこのツリーの更新にいくつかの制約を課しています。

• ノードには追加順に番号（オーダー）を割り振り、ツリーの上から下、左から右（または逆）にその順序が維持されていること
• その順序通りにノードの重みが降順で並んでいること
• 葉ではないノードの重みは左右の子ノードの重みの合計

まず言葉で説明してもよくわからないと思うのでどのようなツリーになるのかを以下のデモで確認してみてください。
以下のデモの左上のテキスト欄にエンコードしたい文字列を入力してGO!!ボタンを押してください。（可視化に使っているvis.jsが結構重いのでワンフレーズくらいがちょうどいいです。）
そうするとresult欄にエンコード結果が出力され、更にグラフが表示されます。このグラフは左右キーを押すことで1ステップずつツリーの変化を確認できます。

See the Pen Untitled by z0ero (@z0ero) on CodePen.

一文字を入力してツリーを更新するフローです。mermaidはやっぱりレイアウトが制御できなくて変な形になりますね・・・

チャート中にNYTというワードが出てきましたが、これはNYTノード(not yet transmitted)と言って適応型ハフマン特有のノード表現です。
ツリーの中に必ず1つ存在している特殊ノードでエンコード時には新規ノードを追加するポイントとなり、デコード時にもツリーを辿ってNYTに辿り着いたら新規ノードの追加を意味するノードとして機能します。これのおかげで次の文字が新規の文字かどうかを判定するために余分なビットを使わずに済みます。

c++実装

これまでを踏まえてc++でパフォーマンスも考慮しつつ実装してみます。単純にするために入力データのビット長が8固定であるとしたコードです。実際には12bitや4bitのデータを圧縮することもあるのでビット長の可変対応も要りますね。

template<size_t MaxBits>
struct AdaptiveHuffman
{
	struct Node
	{
		Node* parent;
		Node* left;
		Node* right;
		uint32_t weight;
		uint8_t leftNode;	// 親に対して左の子なら1
		bool leaf;			// 葉ならtrue

		void swap(Node* n)
		{
			// 元の子ノードの親参照をすり替え
			if (!leaf)
			{
				left->parent = n;
				right->parent = n;
			}
			if (!n->leaf)
			{
				n->left->parent = this;
				n->right->parent = this;
			}
			// 子ポインタとリーフフラグを交換
            auto ref = std::tie(n->left, n->right, n->leaf);
			std::tie(left, right, leaf).swap(, ref);
		}
	};

	std::array<Node, 513> nodes;	// 要素が最大256個なのでツリーノードは高々その2倍で足りる
	Node* NYT;				// not yet transmittedノード。新規追加するときはこのノードに追加する

	AdaptiveHuffman()
		: NYT{ nodes.data() }
	{
		nodes[0] = { .leaf = true };
	}

	// 新規ノードを追加
	Node* allocateNode()
	{
		const auto n = NYT;
		NYT += 2;

		n[0].left = &n[1];
		n[0].right = &n[2];
		n[0].leaf = false;

		// 必ず子ノード2個もセットで追加する
		n[1].parent = n;
		n[1].leftNode = 1;
		n[1].leaf = true;
		n[1].weight = 0;

		n[2].parent = n;
		n[2].leftNode = 0;
		n[2].leaf = true;
		n[2].weight = 0;

		// 追加したうち左(アドレスが若い方)を新ノードとする
		return n + 1;
	}

	// ノードnのウェイトを足してツリー全体も更新する
	void update(Node* n, auto preSwap)
	{
		// ルートのウェイトをあらかじめ足しておくと後の処理の条件をシンプルにできる
		nodes[0].weight++;

		for (; n->parent; n = n->parent)
		{
			// 同じウェイトでかつ最もオーダーの大きいノードを検索
			auto highestOrderInWeightClass = n;
			for (; highestOrderInWeightClass[-1].weight == n->weight; highestOrderInWeightClass--);

			// それがもし自分でも親でもないならそのノードとスワップする
			if (highestOrderInWeightClass != n && highestOrderInWeightClass != n->parent)
			{
				preSwap(highestOrderInWeightClass, n);
				n->swap(highestOrderInWeightClass);
				// ここからはスワップ先のアドレスを辿る
				n = highestOrderInWeightClass;
			}
			// ここでインクリメント
			n->weight++;
		}
	}

	struct Encoder : AdaptiveHuffman
	{
		std::array<Node*, 256> codes{};	// 各文字に対応したノードポインタ

		void encode(BitStream& s, uint8_t b)
		{
			Node* const n = codes[b];
			const bool unknown = n == nullptr;
			if (unknown)
			{
				// 新規要素の追加
				n = codes[b] = allocateNode();
			}

			// このノードのビット列
			std::bitset<256> code;
			uint32_t pos = 0;
			for (auto i = n; i->parent; i = i->parent)
			{
				code[pos++] = i->leftNode != 0;
			}

			// ノード更新
			update(n, [&](Node* highestOrderInWeightClass, Node* n) {
				// 文字→ノード変換マップもスワップに合わせて更新
				if (highestOrderInWeightClass->leaf)
				{
					*std::find(std::begin(codes), std::end(codes), highestOrderInWeightClass) = n;
				}
				if (n->leaf)
				{
					codes[b] = highestOrderInWeightClass;
				}
			});

			// ノードのビット列を書き出し
			// 新規ノードの場合必ず先頭が1なので1bit省ける
			for (uint32_t end = unknown ? 1 : 0; pos != end;)
			{
				s.write(code[--pos], 1);
			}

			// 新規文字だった場合その文字自体もビット列の後に出力
			if (unknown)
			{
				s.write(b, 8);
			}
		}
	};

	struct Decoder : AdaptiveHuffman
	{
		std::array<uint8_t, 512> codes{};	// 各ノードに対応した文字

		uint8_t decode(BitStream& s)
		{
			uint8_t b;
			for (auto n = nodes.data();;)
			{
				if (n->leaf)
				{
					if (NYT == n)
					{
						// 新規ノード
						n = allocateNode();
						b = s.read(8);
						codes[std::distance(&nodes[0], n)] = b;
					}
					else
					{
						// 復元
						b = codes[std::distance(&nodes[0], n)];
					}
					update(n, [&](Node* highestOrderInWeightClass, Node* n) {
						if (highestOrderInWeightClass->leaf || n->leaf)
						{
							std::swap(codes[std::distance(&nodes[0], n)], codes[std::distance(&nodes[0], highestOrderInWeightClass)]);
						}
					});
					break;
				}
				if (s.read(1))
				{
					n = n->left;
				}
				else
				{
					n = n->right;
				}
			}
			return b;
		}
	};
};

使い方としては

// エンコード=================================
AdaptiveHuffman<8>::Encoder encoder;
BitStream output;

// dataはstd::vector<uint8_t>など
for(auto b : data) {
    encoder.encode(output, b);
}

// デコード===================================
AdaptiveHuffman<8>::Decoder decoder;
BitStream input = 圧縮済みデータで初期化しておく;

// dataが予め圧縮前のサイズにresizeされているとする
for(auto& b : data) {
    b = (uint8_t)decoder.decode(input);
}

こんな感じでビットストリームに対して1文字ずつ符号変換して書き込んで行く感じです。
ちなみにBitStreamクラスはこんなものをイメージしてください。

class BitStream
{
public:
    BitStream();
    uint32_t read(size_t bitCount);
    void write(uint32_t value, size_t bitCount);
    // 書き込み内容を取得したり、読み取り内容を設定したり
    std::vector<uint8_t> bytes() const;
    void bytes(const std::vector<uint8_t>&) const;
};

指定されたビット数分ずつ読み書きができる可変長のバイトストリームとして実装します。

ではここからはAdaptiveHuffmanクラスのポイントを3点ほど説明していきます。

Encoder/Decoderクラス

普通に実装するならNodeクラスに文字の値も持たせると思いますが、エンコードとデコードで必要なデータなどが異なるためそれを分けるためにそれぞれ別クラスにしています。
エンコード時は入力文字が既にツリーに登録されているかどうか判定し、されているならそのノードを素早く引き出したいので入力文字から対応するノードを直接引くための辞書としてEncoder::codesというメンバ変数を持っています。
対してデコード時はツリーをトラバースして葉ノードに到達したらそのノードに対応した文字を出力するので、ノード自体に文字を持たせる実装でもいいと思います。今回は私の諸事情でDecoder::codesにノードから文字を引ける辞書を持たせました。ここはちょっと実装微妙かなとは思いますね・・・

ノード配列

ノードは動的に増えていくものですが、最大数が決まっています。そこで最初から最大数分のノードを確保しておいてノード追加時はそこから切り出して使っていけば動作が軽いですね。さらにこの手法にはもう一つ大きな恩恵があってノードにオーダーを持たせる必要がなくなります。
オーダーはノードの追加順を表すものでしたね。ノードを確保していく際にノード配列の0から順番に切り出していけば(AdaptiveHuffman::allocateNode参照)ノードのアドレス・並び順がそのままオーダーになっています。そしてこれはツリー更新時の同じウェイトでかつ最もオーダーの大きいノードを検索とコメントされている箇所で効力を発揮します。
Vitterのルールを思い出してみましょう。ノードはオーダーとウェイトでソートされているのでした。「aaaabbcdefgh」という文字列を入力した場合だとノード配列には以下のように並んでいることになります。上のjsデモに入力してツリーも合わせて確認すると分かりやすいです。

オーダー（インデックス）	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
ウェイト	12	8	4	4	4	2	2	2	2	1	1	1	1	1	1	1	0
文字	root		a			b				e	d	f	c	g		h	NYT

この状態でgが新たに入力されたとすると、gのウェイトである1と同じウェイトのグループで最もオーダーが大きい（インデックスが小さい）ものを探すわけですが、gのポインタは既に分かっているのでそこからポインタをデクリメントしていくだけでノードの検索ができるというわけです。普通にツリー全体から条件に合うノードを探そうと思うと実装もややこしく速度も遅いですが、こうするだけでかなりアドが稼げます。

1ビットケチる

エンコードで符号ビットを書き出す処理で新規ノードの追加だった場合に末尾1bitをケチっています。文字ビット数が8ビットの場合だと最大で256bitケチれますね(笑)かなり微々たるものですが、どちらかというとデコード処理を簡略化するためにこの対応を入れています。
まず素直なデコード処理を考えると、エンコードされたデータはまず必ずビット列'1'と元データの1文字目から始まるので、ルートノードが必ず子持ちの状態からスタートしなければなりません。しかしこれはエンコード時の初期状態と異なるため対称性が崩れてしまいます。（エンコード時はルートノードがNYTノードであり葉ノードであるという状態から開始する）
そこで新規ノードの1ビットケチりが出てきます。新規ノードを追加するときというのは必ず2ノードずつ追加してその内の左が新規ノード、右が次の新規ノードの親になるので新規文字に割り当てられるビット列の末尾は必ず1になるという特性があります。この1ビットを削って符号化したものをデコードしたらどうなるか見てみましょう。

元データabaをケチエンコードしてa0b1を得ました（ケチらなければ1a01b1）。ここから元のデータを復元するステップを確認します。

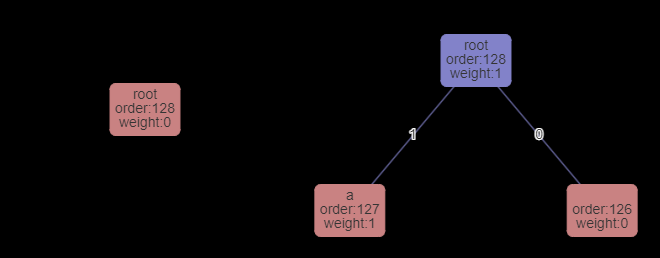
まずルートノードのみの状態からスタートします。（左図）
現在のノードがNYTノードなので入力からaを読み込んでそれをツリーに登録しつつデコード結果として返します。（右図）
次のデコードではルートノードがNYTノードではなくなったので1bit読み込みます。
0が読み込まれたので右のノードへ遷移します。右ノードはNYTなので入力からbを読み込んでツリーに登録・及びデコード結果として返します。（下図へ）

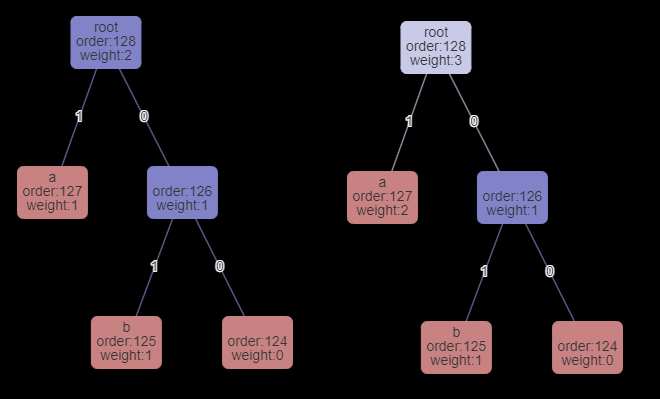
次のデコードでもルートノードがNYTではないので1bit読み込んで1が読み込まれたので左へ遷移します。
そしてNYTではない葉ノードへ到達したのでこの葉の文字aをデコードして返します。
これで無事元のデータabaが復元できることが分かりました。ツリーの初期状態をエンコード時と同じにしようとしたらデータもやや削減できて一石二鳥ですね。