今度こそAdamを超えるのか⁈NeurIPS 2020で注目された「AdaBelief」とは

AdaBeliefとは？

現在、代表的なDeepLearningの最適化アルゴリズムとして、Adamなど適応的な手法や、SGDなど加速的な手法が挙げられます。どの最適化アルゴリズムを選択するかはケースバイケースですが、GANの学習など複雑なケースでは、安定性重視で初手にAdamなど適用的な手法を使う方が多いではないでしょうか。最近NeurIPS2020で採択された論文では、

• Adamのような高速収束性
• SGDのような汎用性
• 学習の安定性

という3つの利点を同時に満たす「AdaBelief」の手法が提案されました。コードも同時にGitHubで公開されています。

論文: https://arxiv.org/abs/2010.07468
GitHub: https://github.com/juntang-zhuang/Adabelief-Optimizer

Adamとの違いは何？

下の図で示したように、AdaBelief（右）とAdam（左）のアルゴリズムがほぼ同じですが、唯一の違いは最後パラメータ更新ルールです。

AdaBeliefでは、勾配の指数移動平均（EMA）を次ステップの勾配の予測値（Belief）とみなし、それに基づいてステップサイズを調整します。具体的には、観測された勾配が予測値から大きく乖離している場合、現在の観測値を信用せず、より小さいステップサイズを採用します。逆に観測された勾配が予測値に近い場合、現在の観測は信頼され、ステップサイズを大きめに調整します。

AdaBeliefのどこが良い？

論文により、Adamと比較したAdaBeliefの強みは、以下2点が挙げられます：

損失関数の曲率も考慮に入れた

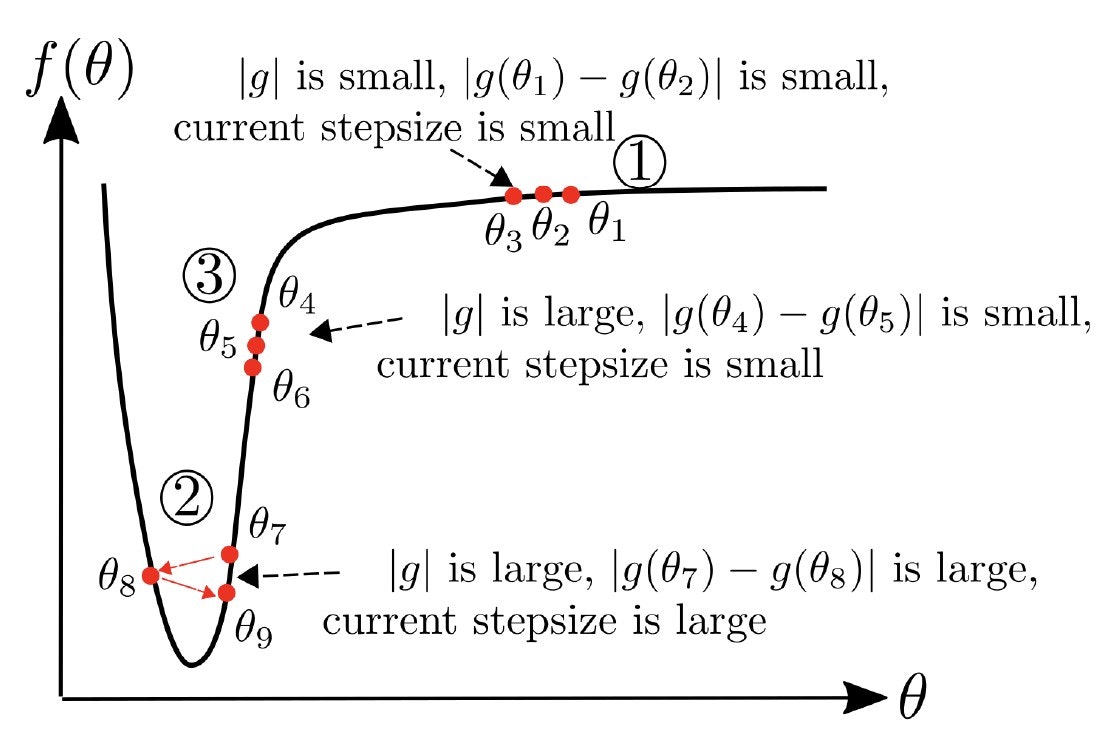
下の図の③部分において、t時刻の勾配 $|g_t|$ は大きいものの、曲率 $|g_t|-|g_{t-1}|$ は小さいため、理想の最適化アルゴリズムとしては大きなステップサイズを採用するところですが、Adamだとステップサイズの分母に含まれる $ v_t $ が大きくなるため、ステップサイズ自体が小さくなる傾向があります。一方AdaBeliefの場合、ステップサイズの分母に含まれる $ s_t $ が曲率に応じて小さくなりますので、理想の最適化アルゴリズムと同じステップサイズを大きめに調整します。

勾配分母の符号も考慮に入れた

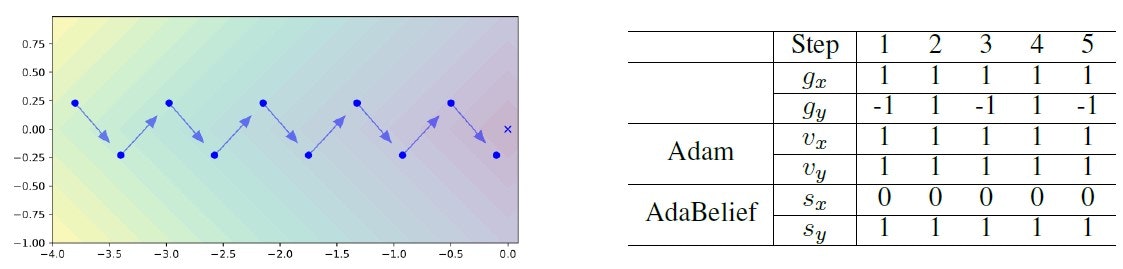
下の図で示した、損失関数が $f(x,y)=|x|+|y|$ の場合において、青い矢印は勾配、「X」マークは最適解を表しています。Adamの場合、$ \sqrt{v_{t,x}} = \sqrt{v_{t,y}} $ のため、X方向とY方向において同じステップサイズを採用しますが、AdaBeliefでは $ \sqrt{s_{t,x}} < \sqrt{v_{t,y}} $ になりますので、Y方向のステップサイズが小さくなり、Y方向の振動を抑える効果があります。

実際の性能はどう？

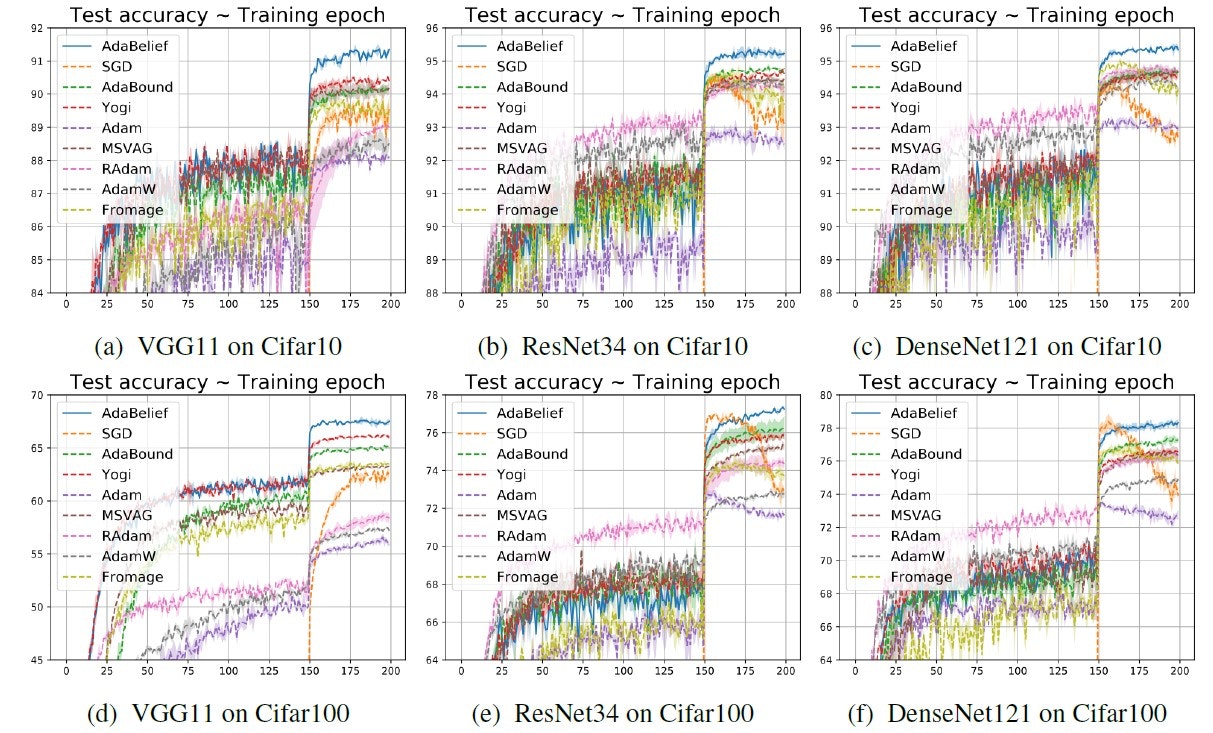
画像分類（CIFAR-10/CIFAR-100）

VGG11、ResNet34、DenseNet121の3つのネットワークを学習させたところ、AdaBeliefはいずれもより良い収束結果を示しました。

画像分類（ImageNet）

Top-1の精度ではSGDに続いて2位になります。

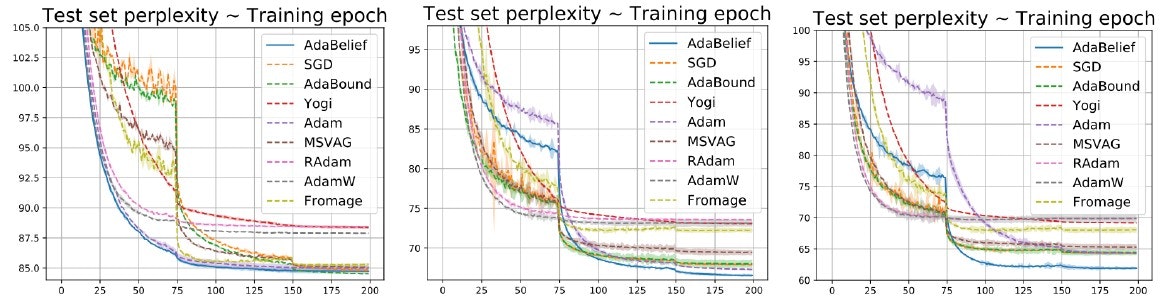
時系列処理（Penn TreeBank）

LSTMで学習した結果、ベンチマーク手法と比較して最小のPerplexityを達成した。

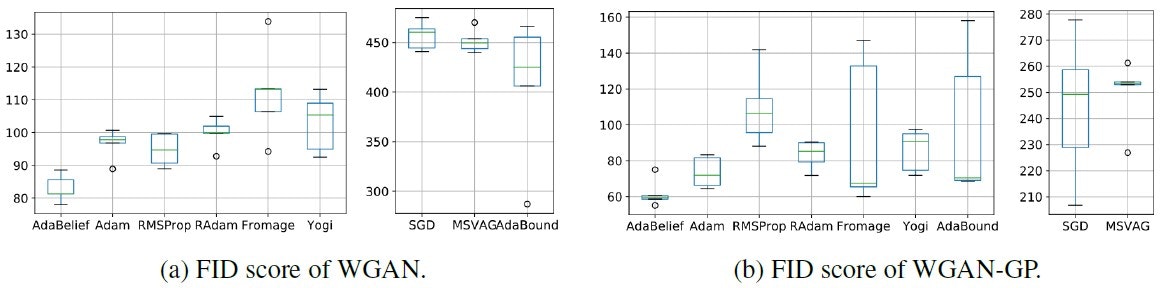
GAN（WGAN/WGAN-GP）

GANの学習においてもAdaBeliefは最小のFIDを達成した。

結局どう使う？

Pytorchの実装はすでに torch-optimizer にインテグレートされています。

import torch_optimizer as optim

# model = ...
optimizer = optim.AdaBelief(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-3,
    weight_decay=0,
    amsgrad=False,
    weight_decouple=False,
    fixed_decay=False,
    rectify=False,
)
optimizer.step()

#まとめ・所感
AdaBeliefはAdamに比べて、新しいハイパーパラメーターも追加せずにここまでの性能を達成できるのは面白いだと思いますが、発想自体は新しくない気がします。（Adamはモメンタム付きRMSpropに例えるなら、AdaBeliefはモメンタム付き [SDProp] (https://www.ijcai.org/Proceedings/2017/0267.pdf)に近いイメージがあります）

近年「Adamを超える」と主張した最適化アルゴリズムがたくさん出てきましたが、本当に超えられるかどうかは時間が証明してくれると思います。

ちなみに、この論文の著者は積極的にエゴサしてるらしく、指摘に対してすぐ回答や再現実験のコードを上げてくれますので、疑問や気になる点があれば遠慮せず論文で記載された連絡先で著者にコンタクトを取ってみてください（笑）。