1. 材料開発とパーシステントホモロジー
材料の分野では、その特性が構造に大きく依存する系が多くあります(e.g. 機械特性、熱特性、電気特性、etc.)。このような場合、一般には構造の代表値(e.g. 平均粒径、含有率、配位数、etc.)と特性の相関を扱うことが多いと思います。
トポロジーに着目してデータのおおまかなカタチを解析する手法を、位相的データ解析(Topological Data Analysis, TDA)と言います。TDAの中でも、データのトポロジカルな特徴を抽出できる強力なツールとして、パーシステントホモロジーが期待されています。
材料組織の特徴量を抽出する手法として、畳み込みニューラルネットワークを用いる場合もあります。このような手法と比較して、パーシステントホモロジーは構造の特徴をマルチスケールに抽出できること、回転にロバストな点などにおいて優位な気がします。
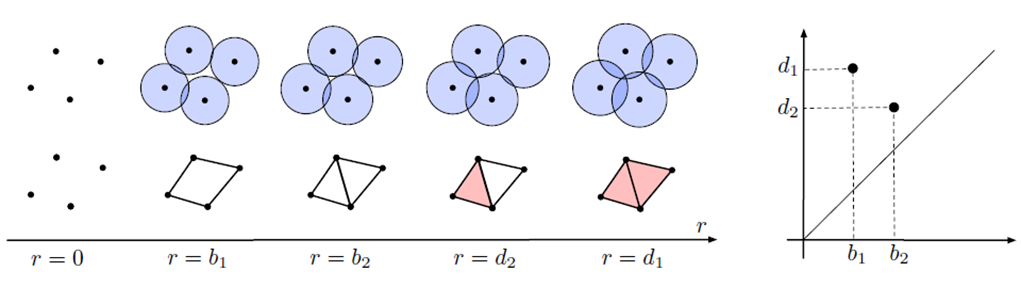
パーシステントホモロジーの模式図
Obayashi Ippei, et al., Journal of Applied and Computational Topology 1 (2018): 421-449. より
概念としては近いですが、二次元(SEM像、光学顕微鏡像、AFM像、etc.)や三次元(X線CT像、etc.)の二値化像ではこのようにデータを扱います。
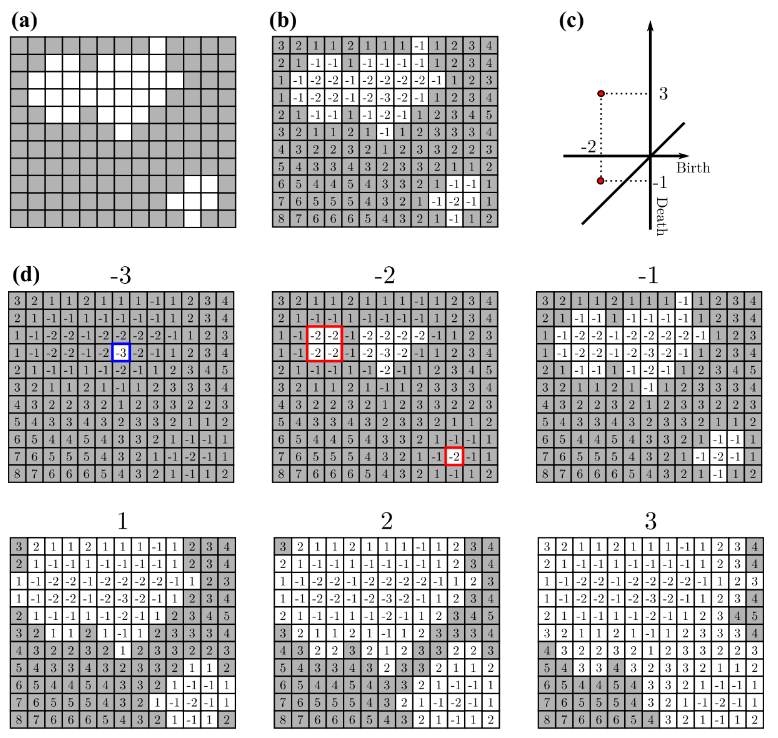
バイナリーイメージのフィルトレーションの模式図
Obayashi Ippei, et al., Journal of Applied and Computational Topology 1 (2018): 421-449. より
(a)にオリジナル画像を、(b)にマンハッタン距離を示しています。例えば、0次のパーシステントダイアグラムでは、データの「つながり」を考えます。(birth, death)がそれぞれ(-2,-1)、(-2,3)のときに島のbirthとdeathが生じています。ただし、マンハッタン距離が-3のとき、青の四角で表した島は除外しています。
今回はパーシステントホモロジーで粒子の構造がどのように可視化できるか試してみます。
2. Homcloud
パーシステントホモロジーを実行するために、HomCloudを利用しました。解説やチュートリアルが豊富で、素人には大変助かりました...
より詳細には、以下の論文などを参考にしてください。
Obayashi, Ippei, Takenobu Nakamura, and Yasuaki Hiraoka, journal of the physical society of japan 91.9 (2022): 091013.
3. データセット
下記サイトから、Ottawa砂とAngular砂を圧縮させた際のX線CT像のデータを使います。
CT像をgifにして確認してみましょう。
左から順に、0、2、6.1、10.2MPaで圧縮したものです。
Ottawa砂
Angular砂
Ottawa砂とAngular砂は粒の形状から簡単に分離できそうです。
同種の砂の場合、圧力による構造の違いはわかりません。
このデータを適当な閾値で二値化して以降の処理を実行します。
4. 構造のベクトル化と主成分分析
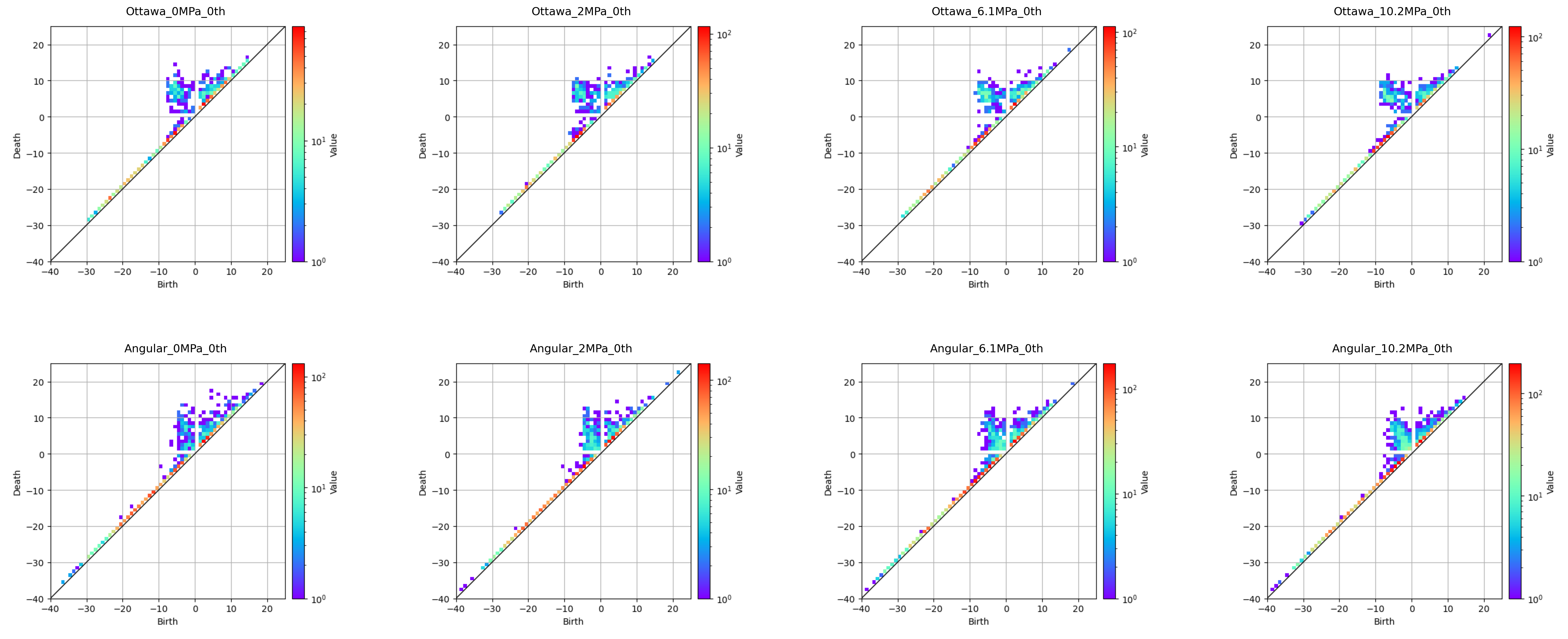
4.1. パーシステントダイアグラム
1次のパーシステントダイアグラムを見てみます。
birthとdeathのヒストグラムを確認できました。今回は1次のパーシステントダイアグラムなので、なんらかのリング構造を見ているはずです。
4.2. 主成分分析
HomCloudのチュートリアルにもありますが、パーシステントダイアグラムのベクトル化にはこちらの文献を参考にしています。
拙い理解ですが、ガウシアンを用いてパーシステントダイアグラムの「ぼやけた」行列を得る->平坦化してベクトル化...という操作になっていると思います。パーシステントダイアグラムの小さな変化に対してロバストであり、機械学習タスクに活用することができます。
このようにして得たベクトルに対し主成分分析を行い、二次元空間に射影してみましょう。
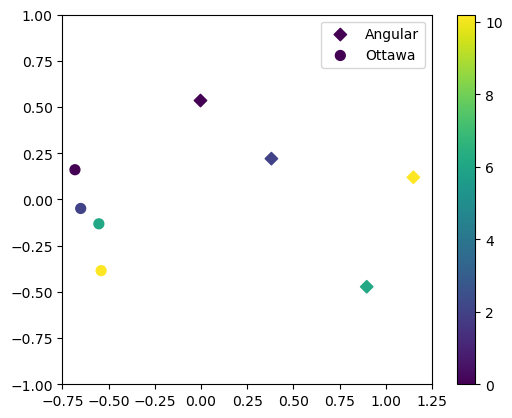
●でOttawa砂を、◆でAngular砂をプロットしています。また、カラーバーで圧力を示しています。パーシステントホモロジーによって構造の特徴を抽出することで、Ottawa砂とAngular砂を分類し、かつ異なる圧力における構造の違いも捉えられているようです。本来であれば、もう少しn数が多いと良かったのですが、今回はたかだか350x350x350のデータでしたので、分割などはせずにn=1で行っています。
実際の材料設計においては、今回の構造のベクトル化に加えて、特性や原料あるいはプロセス条件などを組み合わせることで、予測・回帰・最適化などの機械学習タスクが可能です。また、構造のベクトルからパーシステントダイアグラム、構造データまで逆解析を行うことで、実どのような構造が特性に影響を及ぼしているか可視化することも可能です。