はじめに
Bitcoinはブロックチェーンと呼ばれるある種のデータベースに全ての送金記録が残る暗号通貨である。このような仕組みのため、匿名送金を行うためには第三者を介する必要があった。つまり一旦第三者へ送金したのちに、その第三者がその送金とは別のBitcoinをターゲットへ送金するという方法で匿名性を実装していた。自然な直観として、この方法において第三者は(1)Bitcoinの持ち逃げが可能であり、また(2)この第三者は誰が誰へ送金したかという記録を持ってしまう。TumbleBitとは第三者を介しつつも、この第三者はBitcoinの持ち逃げ・送金の追跡のどちらもできないという優れた匿名送金の方法である。匿名送金が可能であれば、これを相互に行うことで資金洗浄も可能であると考えられ、Bitcoinの使い方を拡張する画期的な技術になると筆者は考えている。
この記事ではまず暗号技術の基礎的なことについて軽く説明し、次にBitcoinの技術的な部分ついて説明する。そしてTumbleBitの論文に基づきTumbleBitについて解説し、最後にまとめを述べる。
この記事を読んで不明な点や質問、改善するべきところなどを見つけた場合は気軽にコメントで教えてほしい。
暗号技術
この章ではTumbleBitを理解するために必要な次の暗号技術について軽く説明する。
- RSA暗号
- ハッシュ関数
- 対称鍵暗号
- 署名
RSA暗号
次は公開鍵暗号RSAにおける平文$x$の暗号化であり、公開鍵$(e, N)$を用いて次のように定義される。
$$
x^e \bmod{N}
$$
また、秘密鍵$d$を用いて暗号文$y$を復号する操作を次のように定義する。
$$
y^d \bmod{N}
$$
そして次がなりたつ。
$$
\left(x^e\right)^d \equiv \left(x^d\right)^e \equiv x \pmod{N}
$$
RSA暗号は公開鍵から暗号文を復号することはできない。また、仮に平文と暗号文と公開鍵の組を持っていたとしても、それらから秘密鍵を推測することはできない。
ハッシュ関数
アリスとボブの2人の間にはハッシュ関数$H$が共有されているものとする。ある値$x$のハッシュ値$H(x)$があるとき、$x$のことをハッシュ値$H(x)$の原像と呼ぶ。
この記事で利用するハッシュ関数はBitcoinのスクリプトで実行できるSHA-256またはRIPEMD-160でなければならない。
対称鍵暗号
アリスとボブの2人の間には対称鍵暗号の関数$\text{Enc}$が共有されているものとする。この関数は対称鍵$k$を用いてデータ$x$を暗号化して暗号文を得る場合、次のように表記する。
\def\Enc#1#2{\text{Enc}_{#1}\left(#2\right)}
\def\Dec#1#2{\text{Dec}_{#1}\left(#2\right)}
\Enc{k}{x}
また、復号関数を$\text{Dec}$とすると、次が成り立つ。
\Dec{k}{\Enc{k}{x}} = x
この関数はたとえばChaCha20などを利用すればよい。
署名
署名とはあるデータに関して次の2つの不正を防ぐために利用される技術である。
- あるデータを他人が作成したと偽る
- 自らが作成したデータを他人が作成したと偽る
まず、あるデータ$x$があり、データ$x$はRSA暗号の公開鍵$(e, N)$に対応する秘密鍵$d$を持つアリスによって作られたものであることをボブに示したいとする。ボブはRSA暗号の公開鍵$(e, N)$を知っているものとし、2人の間にはハッシュ関数$H$が共有されている。このとき次のようなプロトコルを実行すればよい。
- アリスは$h := H(x)$と$s := h^d \bmod N$を計算し$x, s$をボブへ送信する
- ボブは$H(x) = s^e \bmod N$を検証する。このとき$s^e \bmod N$は次のようになる $$ s^e = (h^d)^e = h \pmod{N} $$
このとき、$h^d \bmod N$を計算できるのは秘密鍵$d$を持つアリスだけなので、データ$x$はアリスが意図して作成したことを証明できる。このことから、署名は何かデータと組となってはじめて検証が可能となる。
Bitcoin
Bitcoinはブロックチェーンと呼ばれる全ての送金履歴(トランザクション)を記録した台帳がある。ブロックチェーンは何人ものマイナーによって管理されており、マイナーによってトランザクションが検証され、検証に成功したトランザクションがブロックチェーンに追加される。マイナーには誰もがなることができ、トランザクションを検証した対価としてBitcoinを受け取る。
スクリプト
マイナーはトランザクションに含まれるスクリプトと呼ばれるプログラムを実行し、その結果により有効な送金かどうかを判定する。スクリプトは極めて限定的な、ループや再帰を含まない非チューリング完全なスタックベースのプログラム言語である。たとえば次のスクリプトについて考える。
\begin{array}{l}
1 \\
2 \\
3 \\
\texttt{OP_ADD} \\
\texttt{OP_SUB} \\
\end{array}
%
%
%
\def\AtSOne#1\csod{%
\begin{array}{c|}
\hline
#1\\
\hline
\end{array}
}%
\def\AtSTwo#1,#2\csod{%
\begin{array}{c|c|}
\hline
#1 & #2\\
\hline
\end{array}
}%
\def\SOne#1{\AtSOne#1\csod}
\def\STwo#1{\AtSTwo#1\csod}
\def\AtSThree#1,#2,#3\csod{%
\begin{array}{c|c|c|}
\hline
#1 & #2 & #3\\
\hline
\end{array}
}%
\def\AtSFour#1,#2,#3,#4\csod{%
\begin{array}{c|c|c|c|}
\hline
#1 & #2 & #3 & #4\\
\hline
\end{array}
}%
\def\AtSFive#1,#2,#3,#4,#5\csod{%
\begin{array}{c|c|c|c|c|}
\hline
#1 & #2 & #3 & #4 & #5\\
\hline
\end{array}
}%
\def\AtSSix#1,#2,#3,#4,#5,#6\csod{%
\begin{array}{c|c|c|c|c|c|}
\hline
#1 & #2 & #3 & #4 & #5 & #6\\
\hline
\end{array}
}%
\def\SOne#1{\AtSOne#1\csod}
\def\STwo#1{\AtSTwo#1\csod}
\def\SThree#1{\AtSThree#1\csod}
\def\SFour#1{\AtSFour#1\csod}
\def\SFive#1{\AtSFive#1\csod}
\def\SSix#1{\AtSSix#1\csod}
\def\dosc#1#2\csod{{\rm #1{\scriptsize #2}}}
これは次のように動作する。なお、分かりやすさのために各ステップを実行した後のスタックの状態もあわせて記載する。
- スタックに$1$を追加する $\SOne{1}$
- スタックに$2$を追加する $\STwo{2, 1}$
- スタックに$3$を追加する $\SThree{3, 2, 1}$
- $\texttt{OP_ADD}$によりスタックの先頭から2つを取り出し、 それらを加算した結果をスタックに追加する $\STwo{5, 1}$
- $\texttt{OP_SUB}$によりスタックの先頭から2つを取り出し、 それらを減算した結果をスタックに追加する $\SOne{4}$
さて、もう少し意味のあるBitcoinスクリプトの利用例として、実際の送金を考える。BitcoinのトランザクションはscriptPubKeyとscriptSigという2つのスクリプトを持つ。今、ボブはアリスから貰った1 BTCをチャーリーへ送金しようとしています。アリスからボブへのトランザクションを$\textrm{Tx.1}$として、またボブからチャーリーへのトランザクションを$\textrm{Tx.2}$としたとき、トランザクション$\textrm{Tx.2}$が受理されるための条件は次のようになる。
$\textrm{Tx.2}$の
scriptSigを実行し、そのスタックの状態を引き継いで$\textrm{Tx.1}$のscriptPubKeyを実行する。最終的なスタックの状態が$\SOne{0}$でなければ受理する。
つまり、ブロックチェーンにあるなんらかのscriptPubKeyに対して、スタックマシーンを動作させた結果が$\SOne{0}$以外になるようなscriptSigを作ることができれば、送金を自分など任意のアドレスへ向けることができる。
送金
BitcoinはECDSAと呼ばれる署名アルゴリズムを採用しているが、ECDSAにおいてもRSA暗号を用いた署名においても基礎的な部分に変わりはない。上記の図のように、アリスからボブへ送金された1 BTCをボブがチャーリーへ送金する場合を考える。また、ボブのBitcoinアドレス1に対応する公開鍵を$\mathcal{B}$とする。
まず$\mathrm{Tx.2}$のscriptSigには、送金者ボブの署名$S$2と公開鍵$\mathcal{B}$が次のように入る。
\begin{array}{l}
S \\
\mathcal{B}
\end{array}
これによりスタックの状態は$\STwo{\mathcal{B}, S}$となり、この状態でアリスからボブへの送金を示すトランザクション$\mathrm{Tx.1}$のscriptPubKeyが実行される。このscriptPubKeyは次のようになっている。
\begin{array}{l}
\texttt{OP_DUP} \\
\texttt{OP_HASH160} \\
h \\
\texttt{OP_EQUALVERIFY} \\
\texttt{OP_CHECKSIG} \\
\end{array}
これをスタック$\STwo{\mathcal{B}, S}$の下で実行すると、次のようになる。
- $\texttt{OP_DUP}$によりスタックの先頭をコピーする $\SThree{\mathcal{B}, \mathcal{B}, S}$
- $\texttt{OP_HASH160}$によりスタックの先頭の値のハッシュ値3を計算しそれをスタックの先頭に追加する $\SThree{H(\mathcal{B}), \mathcal{B}, S}$
- スタックの先頭に$h$を追加する $\SFour{h, H(\mathcal{B}), \mathcal{B}, S}$
- $\texttt{OP_EQUALVERIFY}$により、スタックの先頭から2つを取り出しそれらが等しいかを比較する。等しくない場合は直ちに失敗となる $\STwo{\mathcal{B}, S}$
- $\texttt{OP_CHECKSIG}$により、スタックの先頭にある公開鍵を利用してスタックの2番目にある署名を検証する。検証に成功した場合は$1$をスタックの先頭に追加し、失敗した場合は$0$を追加する $\SOne{1}$
このことから、$h = H(\mathcal{B})$かつ公開鍵$\mathcal{B}$で署名$S$を検証できるときに限って上記のスクリプトの実行結果は$\SOne{1}$となり受理される。Bitcoinのスクリプトはこのように署名の検証を行うことで送金が特定のアドレスに届くように制御している。
Time Window
Bitcoinの能力として、特定の時間が経過した後であればアリスが取り出せる、というトランザクションを作ることができる。信頼できる時計を得ることは難しいので、ブロックチェーンの長さを時計とみたてている。たとえば「ブロックチェーンが$n$以上の場合はアリスが取り出せる」というトランザクションを作ることができる。以下はこのようなトランザクションのscriptPubKeyである。
\begin{array}{l}
n \\
\texttt{OP_CHECKLOCKTIMEVERIFY} \\
\texttt{OP_DROP} \\
\mathcal{A} \\
\texttt{OP_CHECKSIG} \\
\end{array}
このscriptPubKeyの動作について説明する。なおスタックにはアリスの署名$S$が積まれているものとする。
- $n$をスタックの先頭に追加する $\STwo{n, \mathcal{A}}$
- $\texttt{OP_CHECKLOCKTIMEVERIFY}$により、
scriptSigが入る予定のブロックがBitcoinのブロックチェーンにおいてスタックの先頭の値と比べて、等しいかより大きいのであれば先頭に$1$を追加し、そうでなければ直ちにトランザクションは失敗となる $\STwo{1, S}$ - $\texttt{OP_DROP}$により、スタックの先頭の値を捨てる $\SOne{S}$
- 公開鍵$\mathcal{A}$をスタックの先頭に追加する $\STwo{\mathcal{A}, S}$
- $\texttt{OP_CHECKSIG}$により、署名を検証する $\SOne{1}$
このようにBitcoinは特定の時間が経過した後に取り出せるという処理を書くことができる。
TumbleBitのプロトコル
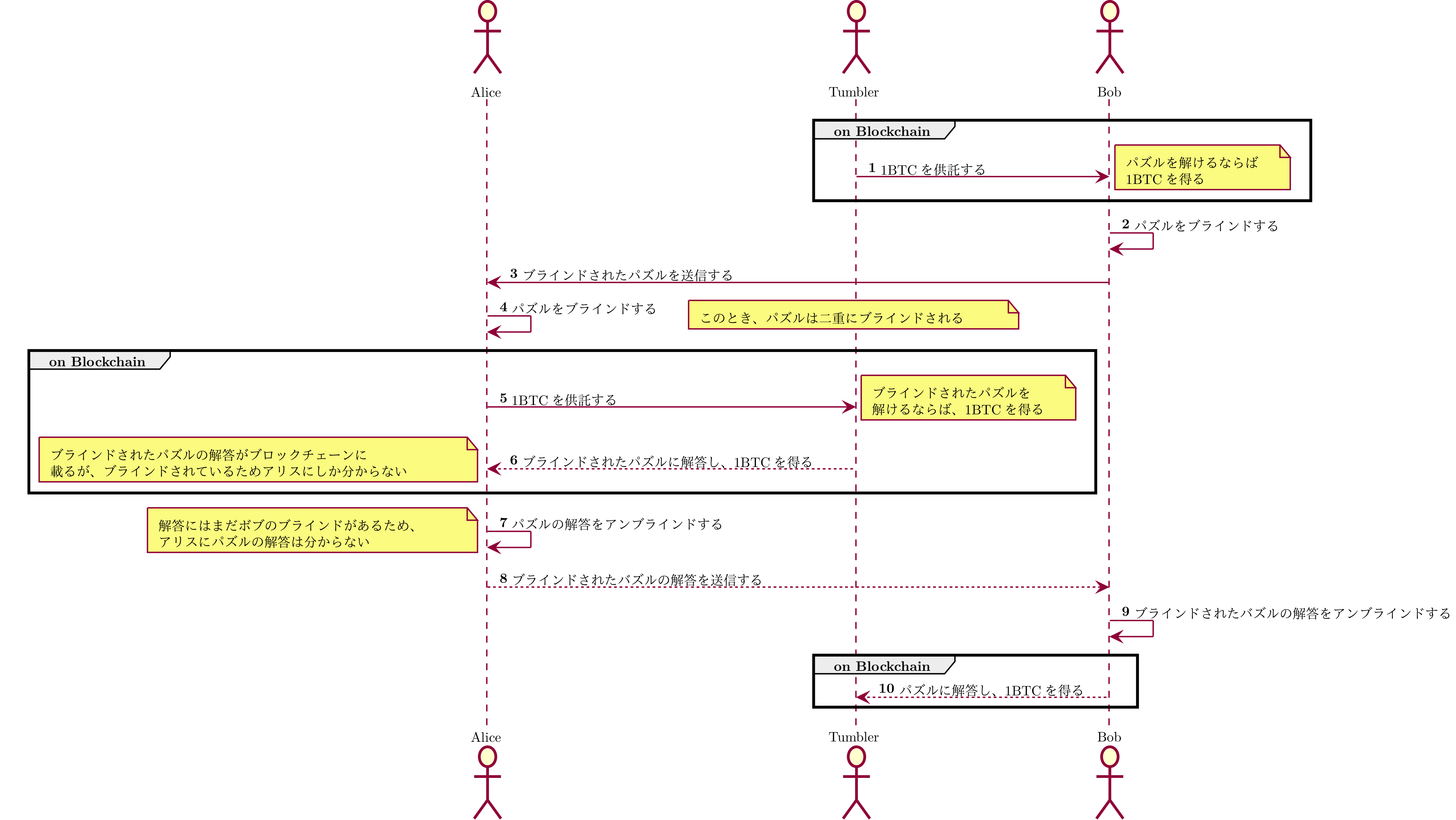
TumbleBitのプロトコルは3つのフェーズからなる。ここではアリスがボブへ匿名送金をしたいと考えているとする。また、ミキシングを行う者としてタンブラー(Tumbler)が存在する。タンブラーは自分の利益を最大にしようとするため、隙があればアリスやボブからお金を奪ったり、あるいはアリスからボブの送金を追跡したりする。そして、今アリスはボブへ1 BTCを匿名で送信したいと考えているものとする。全体的なTumbleBitのプロトコルの概要は次の図の通りである4。
これを文字で詳しく書くと次のようになる。
- タンブラーは1 BTCをブロックチェーン上に供託する
- もしボブの署名とパズルの解答を含むトランザクションを送信できるならば、この1 BTCを得ることができる
- この供託はしばらく時間が経ったのち、タンブラーが回収することができる
- ボブはパズルをボブのものと分からないようにブラインドする
- ブラインドしてもタンブラーはパズルを解くことができるが、ボブ以外の者はブラインドされたパズルがボブへ送信されたものかどうかが分からない
- ボブはブラインドされたパズルをアリスへ送信する
- アリスはボブから送信されたパズルをボブのものと分からないようにブラインドする
- このときパズルは二重にブラインドされるが、二重にブラインドされたとしてもタンブラーはパズルを解くことができる
- アリスは1 BTCをブロックチェーンへ供託する
- タンブラーの署名と二重にブラインドされたパズルの解答を含むトランザクションを送信できるならば、この1 BTCを得ることができる
- この供託はしばらく時間が経ったのち、アリスが回収することができる
- タンブラーは自身の署名と二重にブラインドされたパズルの解答を含むトランザクションを送信し、タンブラーは1 BTCを得る
- これにより二重にブラインドされたパズルの解答がブロックチェーン上に掲載されるが、二重にブラインドされたパズルの解答では(1)のパズルを解くことができない
- アリスはブロックチェーン上の二重にブラインドされたパズルの解答をアンブラインドし、ブラインドされたパズルの解答を得る
- この解答はボブのブラインドがあるため、アリスは(1)の供託を奪うことができない
- アリスはボブへブラインドされたパズルの解答を送信する
- ボブはブラインドされたパズルの解答をアンブラインドし、パズルの解答を得る
- ボブは(9)で得たパズルの解答を利用して、(1)のトランザクションから1 BTCを引き出す
このようにアリスの1 BTCがタンブラーに渡り、タンブラーの1 BTCがボブへ渡っているためBitcoinのブロックチェーンを追跡したとしてもアリスからボブへ送金されたということは分からない。
ただし、今回説明では簡単のため、各トランザクションに付けるべきTime Windowは省略した。実際にはアリス・ボブ・タンブラーは誰がいつ消え失せてもおかしくないため、適切に供託を回収できるようにTime Windowを設定しなければならない。
1. Puzzle-Promise Protocol
このプロトコルは全体の(1)から(2)まで部分である。ボブとタンブラーはパズルを作る。パズルは次のような性質を持つ。
パズルの答えはタンブラー自身にしか分からないが、もし解答できるならばその解答を利用してタンブラーが供託した1 BTCを得ることができる。
まず、準備としてタンブラーは1度しか使わないBitcoinの署名アルゴリズムであるECDSAの秘密鍵$SK_{T}^{eph}$と公開鍵$PK_{T}^{eph}$を用意する。この公開鍵$PK_{T}^{eph}$はボブも知っている。また、タンブラーは自身のRSA暗号の秘密鍵$d$を知っており、またその公開鍵$(e, N)$はボブとタンブラーの2人ともが知っている。そして次のようなパズルを次のように作成する。
-
タンブラーは未署名のトランザクション$\mathrm{Tx.1}$をボブへ送信する
- このトランザクション$\mathrm{Tx.1}$は「秘密鍵$SK_{T}^{eph}$による署名とボブのBitcoin秘密鍵の署名の両方を含む、
scriptSigにより送金できる」というscriptPubKeyを持つ。具体的なスクリプトは次のようになる
\begin{array}{l} 2 \\ PK_{T}^{eph} \\ \mathcal{B} \\ 2 \\ \texttt{OP_CHECKMULTISIG} \end{array} - このトランザクション$\mathrm{Tx.1}$は「秘密鍵$SK_{T}^{eph}$による署名とボブのBitcoin秘密鍵の署名の両方を含む、
-
ボブは$\mu$個の未署名のトランザクション列$R := \{\textrm{Tx}^{cash}_1, \dots \textrm{Tx}^{cash}_{\mu}\}$を作成する
- このトランザクションは$\mathrm{Tx.1}$からお金を取り出す次のような
scriptSigを持つ
\def\SH{\left\langle \text{Signature Hole}\right\rangle} \begin{array}{l} \SH \\ S_{B} \end{array}- ただし$\SH$は署名を入れるための空白である
- また、この未署名トランザクション列のひとつひとつの値のハッシュ値を$ht_i := H(\textrm{Tx}^{cash}_1) \; (i := 1, \dots, \mu)$とする
- さらに$salt$をソルトとして、未署名トランザクション列$R$に対するハッシュ値を$h_R := H(salt \mid\mid \{ht_1, \dots, ht_{\mu}\})$とする
- このトランザクションは$\mathrm{Tx.1}$からお金を取り出す次のような
-
ボブは$\eta$個の乱数列$F := \{r_1, \dots r_{\eta}\}$を作成し、乱数列からハッシュ値$ft_i := H(r_i) \; (i := 1, \dots, \eta)$を計算する
- また乱数列$F$に対するハッシュ値を$h_F := H(salt \mid\mid \{ft_1, \dots, ft_{\eta}\})$とする
ボブは$ht_i, ft_j \; (i = 1, \dots, \mu; j = 1, \dots \eta)$の要素を結合してランダムに並び換えた列$\beta := \{\beta_1, \dots, \beta_{\mu + \eta}\}$を作成する
-
ボブは次のデータをタンブラーへ送信する
- データ列$\{\beta_1, \dots, \beta_{\mu + \eta}\}$
- ハッシュ値$h_R, h_F$
タンブラーは$\{\beta_1, \dots, \beta_{\mu + \eta}\}$に秘密鍵$SK_{T}^{eph}$で署名し、その列を$\{\sigma_1, \dots, \sigma_{\mu + \eta}\}$とする
-
タンブラーは署名$\{\sigma_1, \dots, \sigma_{\mu + \eta}\}$を対称鍵暗号で暗号化する
- このときの対象鍵を$\{\epsilon_1, \dots, \epsilon_{\mu + \eta}\}$とし、また暗号文を$\{c_1, \dots, c_{\mu + \eta}\}$とする
-
タンブラーは対称鍵$\{\epsilon_1, \dots, \epsilon_{\mu + \eta}\}$をRSA暗号で暗号化する
- 暗号文を$\{{z_1, \dots, z_{\mu + \eta}}\}$とし、ただし$z_i := (\epsilon_i)^e \bmod N \; (i := 1, \dots, \mu + \eta)$とする
タンブラーは$\{\left(c_1, z_1\right), \dots, (c_{\mu + \eta}, z_{\mu + \eta})\}$をボブへ送信する
ボブはハッシュ値$\{ft_1, \dots, ft_{\eta}\}$、ソルト$salt$、ハッシュ値$\{ht_1, \dots, ht_{\mu}\}$、乱数列$F$をタンブラーへ送信する
-
タンブラーは次を検証する
- $h_R = H(salt \mid\mid \{ht_1, \dots, ht_{\mu}\})$
- $h_F := H(salt \mid\mid \{ft_1, \dots, ft_{\eta}\})$
- $\beta_i := H(r_i)$
- また、このときタンブラーは$\beta$のうちのどれが乱数のハッシュ値であって、どれがトランザクションのハッシュ値であるかを知る
タンブラーは、$\beta$のうち乱数のハッシュ値に対応する$i$について$\epsilon_i$をボブへ送信する
-
ボブは次を確認する
- $\epsilon_i < N$かつ
- $z_i = (\epsilon_i) \bmod N$かつ
- $c_i$を復号して$\sigma_i := \Dec{\epsilon_i}{c_i}$を得る。このとき$\sigma_i$は公開鍵$PK_{T}^{eph}$で検証に成功する
-
タンブラーは、$\beta$のうちトランザクションのハッシュ値に対応する$j$について、次のような$\{q_2, \dots, q_{\mu}\}$をボブへ送信する
- $q_2 := \frac{\epsilon_{j_2}}{\epsilon_{j_1}}, \dots, q_\mu := \frac{\epsilon_{j_{\mu}}}{\epsilon_{j_{\mu - 1}}}$
-
ボブは次を検証する
- $z_2 = z_1 \cdot (q_2)^e \bmod N \land \dots \land z_\mu = z_{\mu - 1} \cdot (q_\mu)^e \bmod N$
タンブラーは$\mathrm{Tx.1}$をブロックチェーンへ送信する
ボブはパズル$z := z_{j_1}$を得て、乱数$r$を用いてブラインドされたパズル$\tilde{z} := z \cdot (r)^e \bmod N$を計算する
パズルの答えとは、トランザクション$\mathrm{Tx}_{i}^{cash}$に対するタンブラーの署名$\sigma_i$である。この署名$\sigma_i$が得られればボブはトランザクション$\mathrm{Tx.1}$から1 BTCを得ることができる。タンブラーから得られる暗号文$z_i$を復号できればそこから対称鍵暗号の鍵$\epsilon_i$が得られ、それを用いて暗号文$c_i$を復号することで$\sigma_i$が得られる。整理すると次のようになる。
\sigma_i = \Dec{\epsilon_i = (z_i)^d \bmod N}{c_i}
また、ボブとタンブラーの間で本物のトランザクションと偽のトランザクションを作成して、両方をRSA暗号で一旦復号させる、といった手法を用いている。この手法はCut-and-Chooseプロトコルと呼ばれており、これにより次の2つの不正を高い確率で防ぐことができる。
- ボブがタンブラーの署名を無料で入手してしまう
- タンブラーが解読不能なパズルを作成してしまう
なぜこれらが防げるのかというと、まず前者が成功するためにはボブは$F$の中に本物のトランザクションを紛れこませるしかない。しかし、(10)でタンブラー内容を公開したときに不正が明らかになってしまうため、ボブは不正をすることができない。また、後者のタンブラーの不正であるが、これをするためにはタンブラーが次のような確率的ゲームに勝利する必要がある。
$\beta$に含まれる$F$だけをボブの検証が通過するよう本物の署名をし、一方で$R$については解読できないように偽の署名をする
しかし、タンブラーは署名をする時点では$\beta$の中のどこに$R$の要素があり、どこに$F$の要素があるか分からない。つまり成功する確率$P$は$\mu + \eta$個の中から$\eta$を選ぶという組み合せの中の1通りしかないため、次のように表わせる。
P = \frac{1}{{}_{\mu + \eta}C_{\eta}}
従って$\mu, \eta$を適切に設定することでタンブラーの不正は非常に困難にできる。
2. Puzzle-Solving Protocol
このプロトコルは(4)から(8)までに相当し、ボブが手に入れたブラインドされたパズル$\tilde{z}$をアリスへ渡し、アリスはブラインドされたパズルを再度ブラインドし二重にブラインドされたパズルをタンブラーに解答させる。ただし、タンブラーの解答はブロックチェーンに掲載され、解答が正しいことをBitcoinのスクリプトによって検証する。
今、ボブからアリスへブラインドされたパズル$\tilde{z}$が送信されたものとして、またアリスはタンブラーのRSA公開鍵$(e, N)$を知っている。アリスとタンブラーは次のようにパズルの解答を得る。
- アリスは乱数$r_1, \dots, r_m$を利用して二重にブラインドされたパズルの列$R := \{d_1, \dots, d_m\} \; (d_i := \tilde{z} \cdot (r_i)^e \bmod N)$を作成する
- アリスは乱数$\rho_1, \dots, \rho_n$を利用してフェイク列$F := \{\delta_1, \dots, \delta_n\} \; (\delta_j := (\rho)^e \bmod N)$を作成する
- アリスは$R, F$を結合し、ランダムに並びかえた列$\beta := \{\beta_1, \dots, \beta_{m + n}\}$を作成し、タンブラーへ送信する
- タンブラーは$i := 1, \dots m + n$について次を計算する
- $s_i := (\beta_i)^d \bmod N$として乱数$k_i$を対称鍵として暗号文$c_i := \Enc{k_i}{s_i}$
- 対称鍵$k_i$のハッシュ値$h_i := H(k_i)$
- タンブラーは$c_1, \dots, c_{m + n}$と$h_1, \dots, h_{m + n}$をアリスへ送信する
- ボブは$F$と$\rho_1, \dots, \rho_n$をタンブラーへ送信する
- タンブラーは次を検証する。ただし$\beta$上のフェイク列$F$から作成された値のインデックスを特定し、そのインデックスを$i$とする5
- $\beta_i = (\rho_i)^e \bmod N$
- タンブラーは全ての$i$について$k_i$をアリスへ送信する
-
アリスは次を検証する
- $h_i = H(k_i)$
- $s'_i := \Dec{k_i}{c_i}$として$s'_i = \rho_i \bmod N$
- アリスは次のような
scriptPubKeyを持つ1 BTCのトランザクション$\mathrm{Tx.2}$をブロックチェーンへ送信する6。ただし、$h'_1, \dots, h'_m$をここでは$\beta$上のパズルの列のインデックスを$j$とし、$h'_i := h_j \; (i := 1, \dots, m)$である7
\begin{array}{l} \texttt{OP_SHA256} \\ h'_1 \\ \texttt{OP_EQUALVERIFY} \texttt{OP_SHA256} \\ h'_2 \\ \texttt{OP_EQUALVERIFY} \\ \vdots \\ \texttt{OP_SHA256} \\ h'_m \\ \texttt{OP_EQUALVERIFY} \\ \mathcal{T} \\ \texttt{OP_CHECKSIG} \end{array} アリスはタンブラーに$r_1, \dots, r_m$と$\tilde{z}$を送信する
タンブラーは$\beta_j = \tilde{z} \cdot (r_j)^e \bmod N$を確認する
-
タンブラーは次のような
scriptSigを持つトランザクション$\mathrm{Tx.3}$をブロックチェーンへ送信する。ただし$k'_l := k_j \; (l := 1, \dots, m)$\begin{array}{l} k'_1 \\ \vdots \\ k'_m \\ S_{T} \end{array}- このときアリスからタンブラーへ1 BTCが送金される
-
アリスはブロックチェーン上のトランザクション$\mathrm{Tx.2}$から$k_j$を得て、次を検証する
- $s'_j := \Dec{k_j}{c_j}$として$\beta_j = (s'_j)^e \bmod N$
-
アリスは$y_j := s'_j \, / \, r_j$を得る
- $y_j = (\tilde{z})^d \bmod N$となる
アリスは適当な$y \in \{y_1, \dots, y_j\}$をボブへ送信する
このプロトコルでもCut-and-Chooseプロトコルによって、アリスが無料でパズルを解読する不正とタンブラーがパズルを解読せず1 BTCを得る不正を防いでいる。ここでタンブラーはハッシュ値の原像を求めるというパズルを解くことで、1 BTCを得られる。
最後にパズルの答えを得たボブは次のように1 BTCを得る。
- アリスから送信された$y$を用いて、ボブは解答$s := y \, / \, r$を得る
- このとき$s$はトランザクション$Tx_{j}^{cash}$のどれかに対応するタンブラーの秘密鍵$SK_{T}^{eph}$による署名である
-
ボブは次のような
scriptSigを持つトランザクション$\mathrm{Tx.3}$をトランザクションへ送信する\begin{array}{l} s \\ S_{B} \end{array} ボブは1 BTCを得る
まとめ
このようにTumbleBitを使うことで、中間者となる人物にたとえ悪意があったとしても、追跡や資金の持ち逃げができない匿名送金が実現できる。冒頭でも述べたように、この方法を利用すればBitcoinにおける資金洗浄も可能であると思われるので、全ての送金履歴が記録されるBitcoinにおいてこのような技術はBitcoinの使い方を拡張すると思われる。
参考文献
-
Bitcoinアドレスとは署名用の公開鍵をSHA-256でハッシュ値を計算し、そのハッシュ値をRIPEMD-160でもう一度ハッシュ値を計算した後、人間に読みやすいように加工を加えたものである。 ↩
-
このとき署名とは、トランザクションのスクリプト以外のデータのハッシュ値に対する署名となる。 ↩
-
$\texttt{OP_HASH160}$はSHA-256を計算した後、RIPEMD-160を計算するので厳密には二重にハッシュ値を計算するが、本稿では二重の処理を無視して$H$と書くこととする。 ↩
-
パズル、ブラインド、アンブラインドといった用語については後に解説する。 ↩
-
これ以降、変数$i$はこのようなインデックスとする。 ↩
-
ここでは$H$としてSHA-256を選んだものとしてスクリプトを構成した。 ↩
-
これ以降、変数$j$はこのようなインデックスとする。 ↩