Chaum-Pedersenの論文に書いてある方法で、Mental Pokerのカードのドローに必要な部分をすごく端的に書き下してみました。ただ、僕自身が暗号技術に詳しいわけではなく、間違いを含んでいる可能性があるので、興味を持った方は論文をあたる方がいいでしょう。
Mental Pokerのドローは、暗号化された山札からカードを各プレイヤーの秘密鍵で復号化しながらたらい回しにしていきます。この時に各プレイヤーは本当にそのプレイヤーの持つ秘密鍵で復号化したのかどうかというのは、ゲームの公平性に関わる問題です。例えばあるプレイヤーが偽の鍵で復号しているにも関わらず、それが検出できないならば、誰か一人でも不誠実なプレイヤーがいたらもはやゲームが成り立たなくなります。ただ、プレイヤーの鍵を公開してしまうと山札を全て復号化できてしまうので、つまり他のプレイヤーに自分の手札などの情報が分かってしまい、プレイヤーの戦略が流出してしうので、それはよくないです。
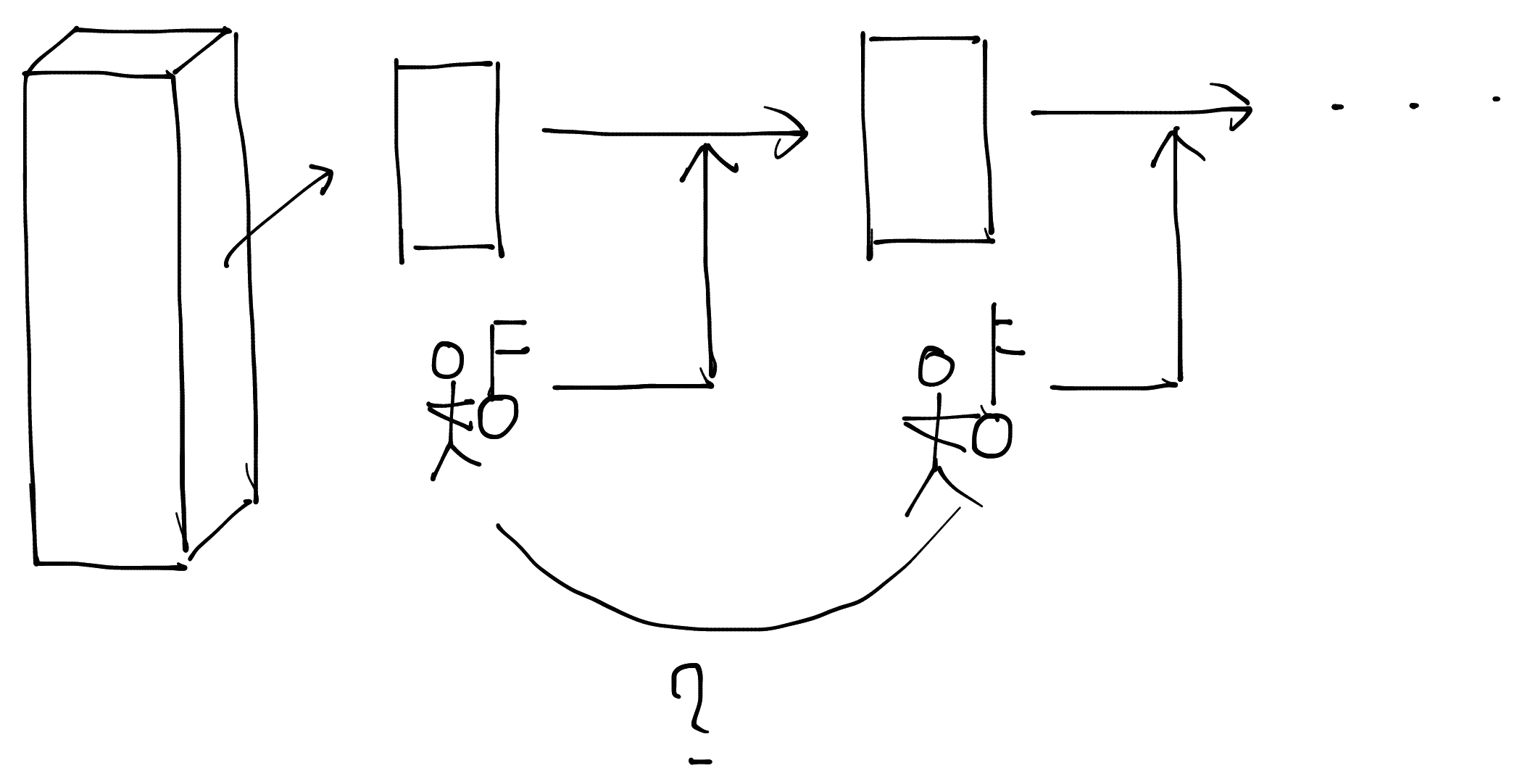
登場人物
- Prover
- 秘密の鍵を使って計算をしたが、その鍵をVerifierには教えずに本当に自分の鍵を使って計算を行なったということを証明したい人
- Verifier
- Proverが本当に自身の鍵を使って計算を行ったのか検証したい人
情報
括弧の中は上記のプロトコルで対応する変数を表わす。
Prover, Verifierが両方とも知っている情報
- $g$
- 特別な性質を持つ乱数($\alpha$)
- $h$
- Proverの公開鍵$g^x$($\beta_i$)
- $z$
- Proverの計算の元になる値($e_{r-1}$)
- $m$
- Proverが秘密鍵$x$を用いて計算したとされる値$z^{x^{-1}}$($e_r$)
Proverしか知らない情報
- $x$
- Proverの秘密鍵($K_i$)
何ができるのか
この手法を使うことで、 Prover の公開鍵を作るのに使われた$x$と、 $m$を計算する時に使われた$x$が同じであることを、 Verifier は$x$を知ることなく確かめられます。つまり、 Verifier は
\log_g{h} \stackrel{?}{=} \log_m{z}
を検証できますが、$\log_g{h}$や$\log_m{z}$の値(つまり Prover の秘密鍵$x$)を突き止めることはできません。
プロトコル
- Prover は乱数$s$を生成して$(a, b) = (g^s, m^s)$を計算し$(a, b)$を Verifier へ送信する
- Verifier は乱数$c$を生成して Prover へ送信する
- Prover は$r = s + cx$を計算して Verifier へ送信する
- Verifier は$g^r \stackrel{?}{=} ah^c$かつ$m^r \stackrel{?}{=} bz^c$を検証する
どういうことか
検証している式
g^r \stackrel{?}{=} ah^c \wedge m^r \stackrel{?}{=} bz^c
は$r = s + cx$なので
g^{s+cx} \stackrel{?}{=} ah^c \wedge m^{s+cx} \stackrel{?}{=} bz^c
と同じです。ここで Verifier は$c$を知っていますが、$s$を知らないので Prover の秘密鍵$x$を$r$から求めることはできません。また、$c$は Verifier によって無作為に選ばれるので Prover が都合のいい数を用意することもできません。
また、$a = g^s, b = m^s$なので
g^{s+cx} \stackrel{?}{=} g^s h^c \wedge m^{s+cx} \stackrel{?}{=} m^s z^c
さらに$h = g^x$であり、$m = z^{x^{-1}}$より$z = m^x$なので
g^{s+cx} \stackrel{?}{=} g^s {g^x}^c \wedge m^{s+cx} \stackrel{?}{=} m^s {m^x}^c \\
g^{s+cx} \stackrel{?}{=} g^{s+cx} \wedge m^{s+cx} \stackrel{?}{=} m^{s+cx}
となるので、 Prover が$h$と$z$、$r$を同じ秘密鍵$x$を用いて計算したならば、この式は真になります。
二回のチャレンジ
Prover が$s$を変更しないまま、 Verifier が異なる乱数$c_1, c_2$を送信して、異なる$r_1, r_2$を入手すると Prover の秘密鍵を突き止めることができます。
今、 Verifier が二つの乱数$c_1, c_2$を送信して、次のような$r_1, r_2$を Prover が返したとします。
r_1 = s + c_1 x \\
r_2 = s + c_2 x
Prover が正しい$x$を用いていた場合、
g^{r_1} = ah^{c_1} \\
g^{r_2} = ah^{c_2}
上の式を下の式で割ると
\frac{g^{r_1}}{g^{r_2}} = \frac{ah^{c_1}}{ah^{c_2}} \\
g^{r_1 - r_2} = h^{c_1 - c_2}
よって
h = g^{\frac{r_1 - r_2}{c_1 - c_2}}
ゆえに
\log_g{h} = \frac{r_1 - r_2}{c_1 - c_2}
$h = g^x$より$\log_g{h} = x$なので$x = \frac{r_1 - r_2}{c_1 - c_2}$となり Verifier に Prover の秘密鍵$x$が計算できてしまいます。
