はじめに
共通鍵暗号などを用いて1対多の通信を行う場合がある。つまり暗号化を行う者は一人であるが、復号は多くのユーザーが行うという場合である。このようなときに一本の鍵で全ての通信を行なうと、その鍵がどこからか流出した際に手が打てなくなってしまう。この記事ではこのような問題を解決する鍵の**失効(Revocation)**を行うための方法をいくつか紹介する。
この記事を読んで疑問に思ったことや、改善するべき点を見つけた場合は気軽にコメントで指摘してほしい。
\def\Enc{\text{Enc}}
直感的な鍵の失効システム
最も直感的な方法は暗号文を受信するユーザーごとに別の鍵で暗号化して、それらを全て送信するという方法である。つまり、$u_1, u_2, \dots, u_N$と$N$人のユーザーが復号したい場合、ユーザー$u_i$の鍵を$K_i$として、送信したいメッセージ$m$に対して次のような暗号文を送信する。
\left(\Enc_{K_1}(m), \Enc_{K_2}(m), \dots, \Enc_{K_N}(m)\right)
このような$N$通りの暗号文を送信すればよい。そして受信したユーザーは$N$組の暗号文の中から自分が復号できるものを順番に試していき、$N$個のうちのひとつを最終的には復号できる。そして、ユーザー$u_i$の鍵が流出した場合、暗号文の組から$K_i$で暗号化したものを排除する。つまり送信者は次のような暗号文を送信する。
\left(\Enc_{K_1}(m), \Enc_{K_2}(m), \dots, \Enc_{K_{i-1}}(m), \Enc_{K_{i+1}}(m), \dots, \Enc_{K_n}(m)\right)
このように、$K_i$で暗号化したデータがないので、$K_i$を持つ攻撃者は暗号文を復号できない。
しかし、この方法にはすぐに分かる課題がある。それは、ユーザーの数$N$に送信するデータ量が比例してしまうということである。従って、この問題を解決する方法について考える。
完全二分木を用いた失効システム
完全二分木を用いて、送信するデータ量を効率化するという方法がある。
セットアップ
まず、次のような鍵とユーザーを対応づける完全二分木を用意する。

そして、各ユーザーにはこの二分木の経路上にある鍵を全て渡しておく。たとえばユーザー$u_1$は鍵$K, K'_1, K''_1$を持つことになり、またユーザー$u_3$は鍵$K, K'_2, K''_3$を持つことになる。
暗号文の送信と鍵の失効
まだいずれの鍵も失効していない場合、送信者は$K$を用いてメッセージ$m$暗号化した次のものを送信すればよい。
\Enc_{K}(m)
次に鍵の失効について考える。いま、$u_3$が持つ鍵の全てが流出したとする。つまり攻撃者は鍵$K, K'_2, K''_3$の全てを知っていることになる。この場合次のようにユーザー$u_3$だけが知らない部分の鍵を用いることができる。

このように、ユーザー$u_1, u_2$は共に$K'_1$を知っているうえ、$u_4$は$K''_4$を知っているので、この2つを使ってメッセージ$m$を暗号化した次のような組を送信すればよい。
\left(\Enc_{K'_1}(m), \Enc_{K''_4}(m)\right)
このようにすることで、最初の直感的なシステムに比べて送信するデータの量を少なくできる。一方で、直感的な方法の場合、受信するユーザーは鍵を一本だけ持てばよかったが、この方法では$\log(N) + 1$の鍵を持つ必要があり、受信するユーザー側のストレージは多く必要であることに注意が必要である。
より効率的な失効システム
完全二分木を用いる方法は効率的ではあるが、失効させるユーザーが増えた場合は暗号文の量が$|\Enc(m)| \times N$に近付いてしまう。そこで、より効率的な方法について議論する。
部分木の一部を削除した要素の集合
まず、具体的な方法の前に部分木を削った集合というものを考える。集合$S_{i, j}$はノード$v_i$の子孫であるノード$v_j$の子孫を全て削除した要素の集合である。

この図の場合、$S_{i, j} = \{v_{i,1}, v_{i,2}, v_{i,3}, v_{i,4}\}$となる。このように、ある部分木から一部を削除してような部分木の集合を$S_{i, j}$と記述する。
送信する暗号文
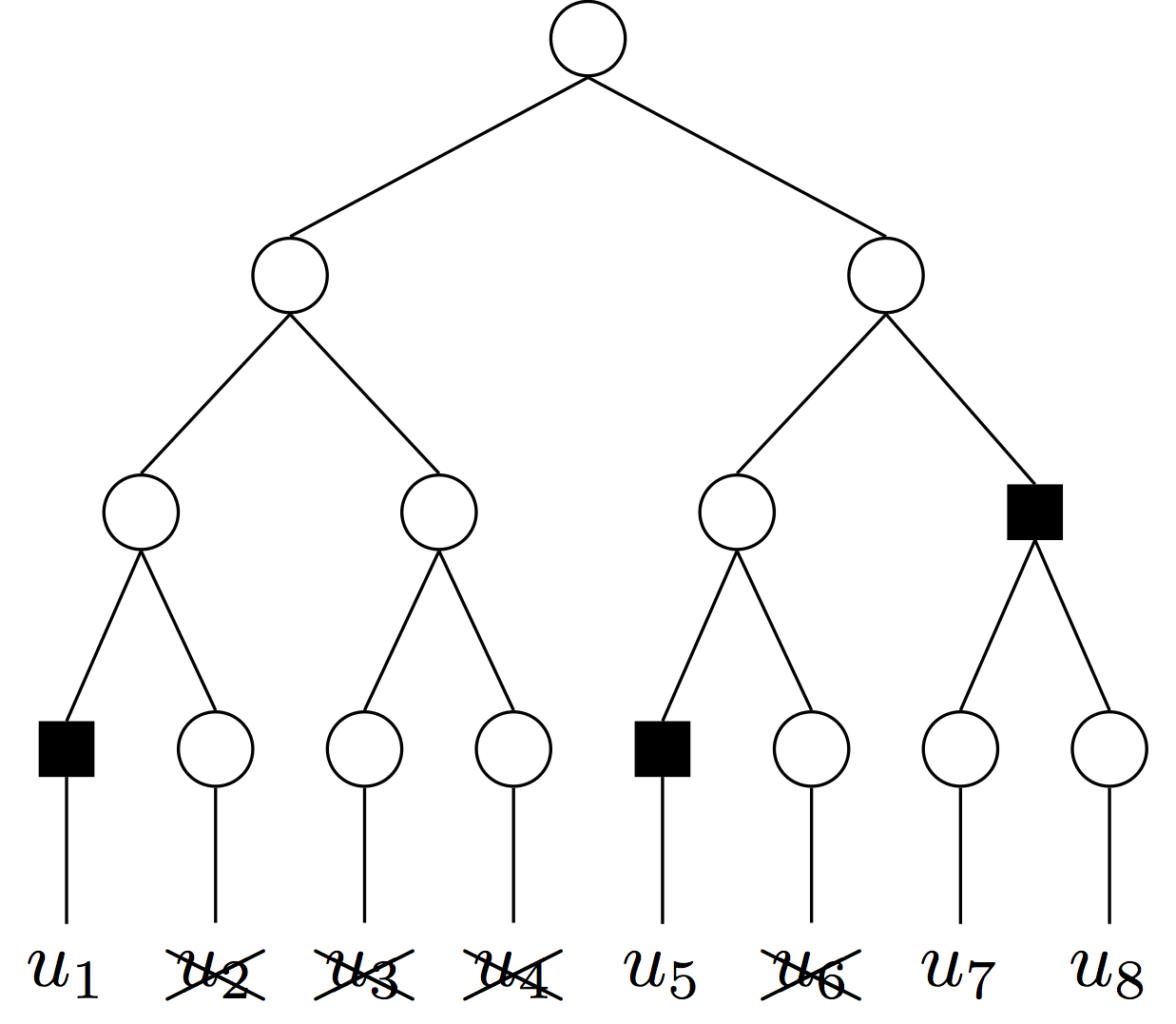
今、次のような木構造があり、この中から4人のユーザーの鍵が失効しているものとする。

完全二分木を用いる方法を用いる場合、次のような3つの鍵で暗号した暗号文が必要になる。
一方で、$S_{i,j}$のような部分木のからある部分木を削除したような集合を考えると次のようになる。

この図では$S_{i,j}$はノード$v_i$からノード$v_j$を削除したものなので、次のようになる。
S_{i,j} = \{v_1\}
また同様に$S_{k,l}$は次のようになる。
S_{k,l} = \{v_2, v_3, v_4\}
このように部分木からその子孫を削除した要素の集合を考えると、通知する情報は$S_{i,j}$と$S_{k,l}$の2つだけでよく、完全二分木よりも効率的になっている。
鍵の生成
さて、次はこのような集合$S_{i,k}$から$S_{i,k}$に所属するユーザーのみが復号できるような鍵を生成する必要がある。鍵を作るために、まずは入力したシードのサイズ$n$ビットに対してその三倍の長さ$3n$ビットを結果を出力する疑似乱数生成器$G$を用意する。そして、次のような補助関数$G_L, G_M, G_L$も導入する。
- $G_L(S)$
- $G(S)$の左側$n$ビットのデータを取得する関数
- $G_M(S)$
- $G(S)$の中央$n$ビットのデータを取得する関数
- $G_R(S)$
- $G(S)$の右側$n$ビットのデータを取得する関数
つまり、これらは次のような関係になっている。
G(S) =
\begin{array}{|c|c|c|}
\hline
G_L(S) & G_M(S) & G_R(S) \\
\hline
\end{array}
これを用いて、次のように全てのノードに対してラベルを振る。

あるノード$i$についてラベル$L = LABEL_i$が割り当てられているとき、その左にある子ノードのラベルは$G_L(L)$となり、右にある子ノードのラベルは$G_R(L)$となる。そして$S_{i,j}$に対応する鍵$L_{i,j}$は、$LABEL_{i,j} = G_R(G_L(L))$を用いて次のようになる。
L_{i,j} = G_M(LABEL_{i,j})
送信者は送信したい集合$S_{i,j}$に対応する鍵$L_{i,j}$で暗号化したメッセージを送信する。
ユーザーが持つ情報
暗号化されたメッセージを復号するために、ユーザーは復号するための情報を持つ必要がある。完全二分木のとき、ユーザーが持っていたのは二分木のルートからの経路上にある鍵であった。今回の効率的なシステムにおいてはあるノード$v_i$があり、その子孫にユーザー$u$がとき、ユーザー$u$はその経路上には_ない_ノード$v_j$のラベル$LABEL_{i,j}$を全て持っている。これはたとえば次の図のようになる。

この場合、$u$はノード$v_{i,1}, v_{i,2}, v_{i,3}, v_{i,4}$のラベルを持っている。このようにすることで、ユーザー$u$は自分が$S_{i,j}$に含まれている場合のみ復号するための鍵$L_{i,j}$を計算できるが、一方で含まれていない場合は$L_{i,j}$を計算することができない。
各ユーザーは深さ$k$の部分木について$k + 1$個のラベルを持つ必要があるので、どの鍵も失効していない時に用いる最初の一本を足して、ユーザーが持つ鍵の総数は次のようになる。
1 + \sum_{k = 1}^{\log(N) + 1}(k - 1)
まとめ
このように、鍵を失効させるための方法を3つ紹介した。完全二分木を用いる方法は失効した鍵が多くなるとメッセージの量が増えてしまうが、最後に紹介した効率的な方法は途端にややこしくなってしまう。従って、鍵を頻繁に失効させなくてもよい場合は、完全二分木を用いた方法を使うのがよいように思える。